X 5 3
interactiveleap
Sep 25, 2025 · 6 min read
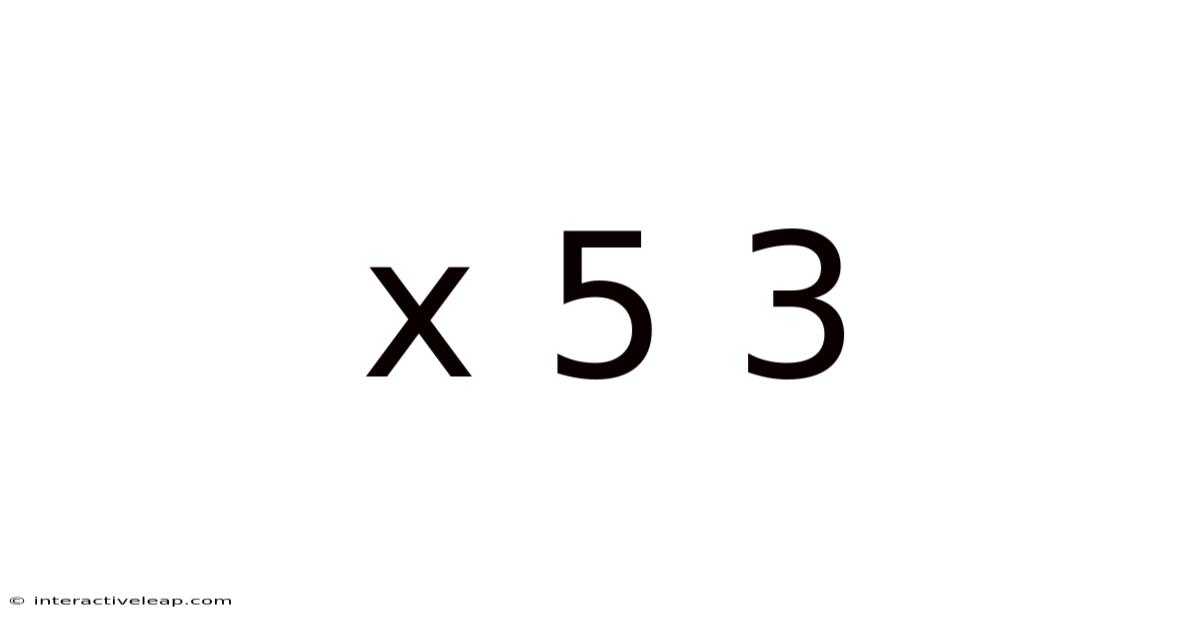
Table of Contents
Decoding x⁵³: Exploring the Mathematical Landscape of Exponentiation and Beyond
This article delves into the fascinating world of mathematical expressions, specifically focusing on the seemingly simple yet surprisingly complex notation "x⁵³". We'll unpack its meaning, explore the underlying principles of exponentiation, examine its applications in various fields, and even venture into related concepts like modular arithmetic and cryptography. Understanding x⁵³ isn't just about solving a mathematical puzzle; it's about grasping fundamental concepts that underpin numerous advanced applications.
Understanding the Basics: Exponentiation
At its core, x⁵³ represents exponentiation, a fundamental operation in mathematics. It signifies x multiplied by itself 53 times. More formally, it's expressed as:
x⁵³ = x * x * x * ... * x (53 times)
This might seem straightforward for smaller values of x and exponents, but the power of exponentiation becomes dramatically apparent as the exponent grows. Even relatively small bases raised to large exponents result in incredibly large numbers. This rapid growth is the foundation of exponential functions, which model many real-world phenomena, from population growth to radioactive decay.
Calculating x⁵³: Practical Considerations and Computational Limits
Calculating x⁵³ directly by repeated multiplication is computationally expensive, especially for large values of x. For instance, if x = 2, then 2⁵³ is a number with sixteen digits (approximately 9.007 x 10¹⁵). While modern computers can handle such calculations relatively quickly, significantly larger values of x or exponents would strain even the most powerful machines.
Therefore, efficient algorithms are crucial for computing large exponentiations. One such method is exponentiation by squaring. This algorithm significantly reduces the number of multiplications required, making calculations more feasible. It works by strategically breaking down the exponent into powers of 2, reducing the number of repeated multiplications.
For example, to calculate x¹⁰, instead of multiplying x ten times, we can square x to get x², then square the result to get x⁴, and finally square that to get x⁸. One more multiplication (x⁸ * x²) gives us x¹⁰. This significantly reduces the computational burden, especially for large exponents like 53.
Beyond Calculation: The Significance of x⁵³ in Different Contexts
The expression x⁵³ transcends simple calculation. Its significance extends to several crucial areas:
-
Algebra and Polynomial Equations: In algebra, x⁵³ can represent a term in a polynomial equation. Solving polynomial equations is a fundamental problem with applications in numerous fields, including engineering, physics, and computer science. The properties of x⁵³ and similar terms are critical to understanding the behavior of these equations.
-
Calculus and Analysis: The expression plays a role in calculus, particularly in finding derivatives and integrals of functions involving powers of x. Understanding its behavior is essential for analyzing the rate of change of quantities and accumulating quantities over time.
-
Number Theory: Number theory studies the properties of numbers, and x⁵³ has a significant place within this field. For example, considering the expression modulo a certain number (modular arithmetic) leads to interesting patterns and applications in cryptography.
-
Cryptography: Modular arithmetic, built upon the principles of exponentiation, is fundamental to many modern encryption techniques. The difficulty of computing discrete logarithms (essentially the inverse of exponentiation) forms the basis of the security of several widely used cryptographic algorithms, including RSA. While x⁵³ itself might not directly appear in a specific cryptographic algorithm, the underlying principles of exponentiation are crucial.
Modular Arithmetic and its Implications
Modular arithmetic, often denoted as x⁵³ (mod n), considers the remainder when x⁵³ is divided by n. This seemingly simple modification opens up a vast array of applications, particularly in cryptography. The reason is that, despite the potentially immense size of x⁵³ for large x, the remainder (the result of the modulo operation) is always within a limited range (0 to n-1). This confined space allows for efficient computations and provides the foundation for secure communication protocols.
For example, in RSA cryptography, a large exponent (e) is used to encrypt a message (m) as mᵉ (mod n). The decryption process utilizes the modular multiplicative inverse of the exponent, ensuring that the original message can be recovered. The security of RSA relies heavily on the computational difficulty of determining the prime factors of n, and the properties of modular exponentiation are central to this security.
Exploring Related Concepts
The study of x⁵³ leads us to explore several related concepts:
-
Logarithms: The inverse operation of exponentiation is the logarithm. If y = x⁵³, then the logarithm base x of y (logₓ y) is 53. Logarithms are essential tools for simplifying calculations and solving equations involving exponents.
-
Complex Numbers: While x⁵³ is typically considered for real numbers x, it can also be extended to complex numbers. Complex numbers are numbers of the form a + bi, where a and b are real numbers and i is the imaginary unit (√-1). The behavior of x⁵³ for complex x has interesting properties and applications in areas such as signal processing and quantum mechanics.
-
Infinite Series: Exponentiation can be expressed using infinite series (Taylor series or Maclaurin series), providing a way to approximate its value for certain ranges of x. These series are powerful tools for approximating functions and solving differential equations.
Frequently Asked Questions (FAQ)
Q: What is the practical limit for calculating x⁵³?
A: The practical limit depends on the computing power available. While modern computers can handle fairly large values of x, exceedingly large numbers can still exceed available memory or processing capabilities. Efficient algorithms like exponentiation by squaring mitigate this limitation to some extent.
Q: Are there any real-world applications of x⁵³ directly?
A: While x⁵³ itself may not be explicitly used in many everyday applications, the underlying principles of exponentiation are widespread. It underlies exponential growth models in finance, biology, and physics. The related concepts of modular arithmetic and logarithms have direct applications in cryptography and data security.
Q: How does the choice of base (x) affect the outcome?
A: The base x significantly affects the outcome. For x > 1, x⁵³ grows rapidly as x increases. If 0 < x < 1, then x⁵³ decreases rapidly towards zero as the exponent is large. If x = 1, then x⁵³ always equals 1. For x = 0, x⁵³ is always 0, and if x is negative, the sign of the result alternates depending on whether the exponent is odd or even.
Q: Can x⁵³ be negative?
A: Yes, if x is negative and the exponent 53 is odd, the result will be negative. If x is negative and the exponent is even, the result will be positive.
Q: What are the potential challenges in working with x⁵³?
A: The main challenges are computational limitations for very large values of x, and the potential for overflow errors when dealing with extremely large numbers. Efficient algorithms and appropriate data types are crucial to mitigate these issues.
Conclusion: A Deeper Dive into the Fundamentals
The seemingly simple expression x⁵³ opens a door to a vast landscape of mathematical concepts. From the fundamental principles of exponentiation to the sophisticated applications in cryptography and beyond, understanding its implications is crucial for anyone seeking a deeper appreciation of mathematics and its impact on our world. This exploration emphasizes not just the calculation but the underlying theory and its significance in various fields, highlighting the power and beauty of mathematical reasoning. The journey of understanding x⁵³ is not just about obtaining a numerical result; it’s about mastering fundamental principles that underpin much of modern science and technology.
Latest Posts
Latest Posts
-
3 2x 5
Sep 25, 2025
-
20 Of 31 00
Sep 25, 2025
-
130mm In Inches
Sep 25, 2025
-
Do Eyeballs Grow
Sep 25, 2025
-
60 Of 37
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about X 5 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.