3 2x 5
interactiveleap
Sep 25, 2025 · 6 min read
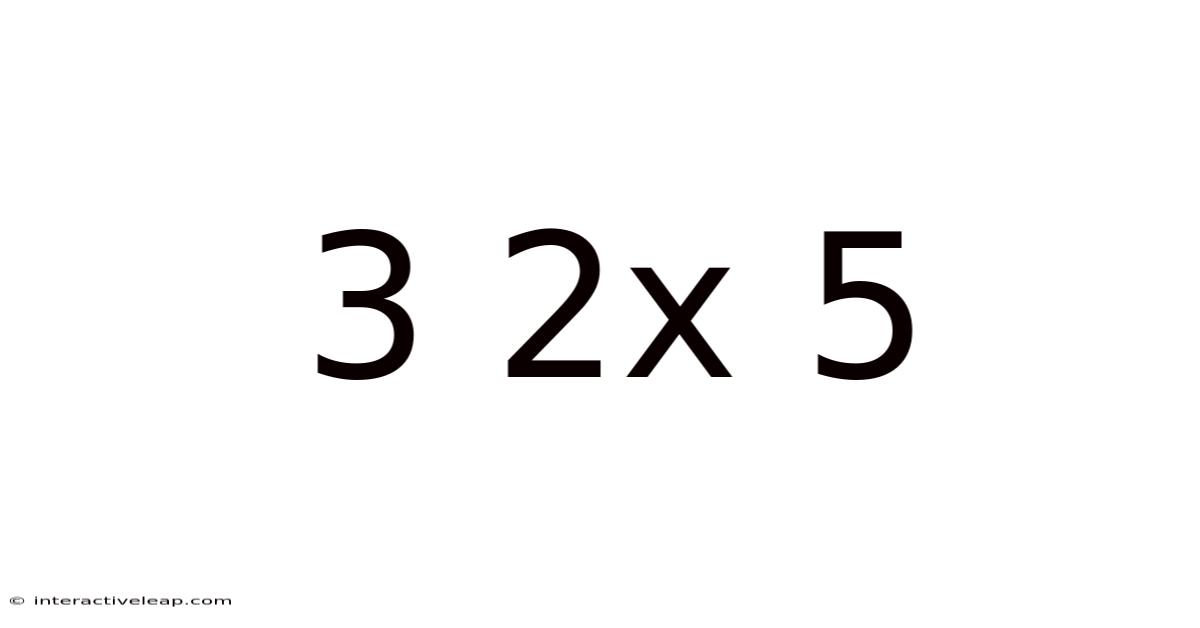
Table of Contents
Decoding 3 x 2 x 5: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "3 x 2 x 5," delving beyond the immediate answer to uncover the fundamental principles of multiplication, its practical applications across various fields, and the broader mathematical concepts it embodies. We'll unravel the magic behind this calculation, illustrating its relevance in everyday life and advanced studies. Understanding this seemingly basic equation lays a crucial foundation for grasping more complex mathematical concepts.
Introduction: The Power of Multiplication
At its core, 3 x 2 x 5 represents a multiplication problem. Multiplication is a fundamental arithmetic operation that involves repeated addition. In this case, we are multiplying three numbers: 3, 2, and 5. The result, 30, is obtained by successively multiplying these numbers. This simple equation, however, opens doors to a world of mathematical possibilities, showcasing the power of repeated addition and the commutative, associative, and distributive properties of multiplication. This exploration will go beyond simply calculating the answer; we will examine the underlying principles and real-world applications.
Step-by-Step Calculation: Unraveling 3 x 2 x 5
The beauty of multiplication lies in its flexibility. We can solve 3 x 2 x 5 in several ways, thanks to the associative property, which states that the grouping of numbers in a multiplication problem doesn't change the final result. Here are a few approaches:
-
Method 1: Left-to-Right: We can start by multiplying 3 and 2, then multiplying the result by 5: (3 x 2) x 5 = 6 x 5 = 30
-
Method 2: Right-to-Left: Alternatively, we can begin with 2 x 5 and then multiply the result by 3: 3 x (2 x 5) = 3 x 10 = 30
-
Method 3: Any Order: Due to the commutative property (the order of numbers doesn't affect the product), we could even rearrange the numbers: 5 x 2 x 3 = 10 x 3 = 30. This flexibility highlights the inherent efficiency of multiplication.
These different methods demonstrate the associative and commutative properties, fundamental concepts in algebra and beyond. Understanding these properties allows us to simplify complex calculations and strategize for efficient problem-solving.
The Commutative Property in Action: Rearranging for Efficiency
The commutative property of multiplication states that the order of the numbers being multiplied does not affect the product. This seemingly simple property has significant implications. For instance, in 3 x 2 x 5, we could choose to multiply 2 x 5 first (resulting in 10), which simplifies the subsequent multiplication with 3. This strategic rearrangement illustrates how understanding mathematical properties can lead to faster and more efficient calculations.
The Associative Property and Grouping: Strategic Calculation
The associative property highlights that the grouping of numbers in a multiplication problem doesn't alter the outcome. This is critical for tackling more complex equations. Consider a problem with multiple numbers. The associative property allows you to group the numbers in a way that simplifies the calculation. For instance, consider a slightly larger problem like 4 x 5 x 2 x 3. You might group (4 x 5) x (2 x 3) = 20 x 6 = 120, simplifying the calculation significantly.
Beyond the Calculation: Real-World Applications
The simple calculation 3 x 2 x 5 extends far beyond the realm of theoretical mathematics. Let's explore some practical examples:
-
Everyday Shopping: Imagine buying three packs of cookies, with each pack containing two rows of five cookies. The total number of cookies is 3 x 2 x 5 = 30 cookies.
-
Construction and Measurement: Calculating the area of a rectangular prism (a 3D shape) often involves multiplication. If the prism has dimensions of 3 units by 2 units by 5 units, its volume is 3 x 2 x 5 = 30 cubic units.
-
Data Analysis and Statistics: Multiplication is ubiquitous in data analysis. For example, if you have three groups of data, each containing two sets of measurements with five values each, the total number of data points is 3 x 2 x 5 = 30.
-
Computer Science and Programming: Multiplication is a fundamental operation in computer programming. It's used in algorithms, calculations, and data manipulation across various programming languages.
Expanding the Concept: Linking to Other Mathematical Areas
The simple equation 3 x 2 x 5 provides a springboard for exploring more advanced mathematical concepts:
-
Algebra: The equation can be generalized using variables. For instance, let's say a = 3, b = 2, and c = 5. Then the equation becomes a x b x c = 30. This introduction of variables lays the foundation for algebraic expressions and equations.
-
Geometry: As previously mentioned, calculating the volume of a rectangular prism directly utilizes multiplication. This connection highlights the interdisciplinary nature of mathematics.
-
Number Theory: The factors of 30 (1, 2, 3, 5, 6, 10, 15, 30) lead to explorations of prime numbers, divisibility, and other number theoretical concepts.
-
Calculus: Though not directly apparent in this simple calculation, the principles of multiplication underpin many concepts in calculus, particularly in areas like integration and differentiation.
Frequently Asked Questions (FAQ)
-
Q: What is the most efficient way to calculate 3 x 2 x 5?
-
A: The most efficient method depends on personal preference and familiarity with multiplication tables. Many find multiplying 2 x 5 = 10 first, then 10 x 3 = 30, to be the easiest approach.
-
Q: What are the prime factors of 30?
-
A: The prime factors of 30 are 2, 3, and 5. These are prime numbers that when multiplied together equal 30.
-
Q: How does this simple equation relate to more complex mathematical concepts?
-
A: This seemingly simple equation demonstrates fundamental properties like the commutative and associative properties, forming a building block for understanding more advanced concepts in algebra, geometry, number theory, and even calculus. It showcases how basic operations lay the groundwork for complex mathematical structures.
-
Q: Can I use a calculator for this calculation?
-
A: Certainly! Calculators are useful tools, especially for more complex calculations. However, understanding the underlying principles is crucial for developing mathematical intuition and problem-solving skills.
Conclusion: The Significance of Simple Equations
The seemingly simple equation 3 x 2 x 5 is more than just a basic arithmetic problem. It serves as a gateway to understanding fundamental mathematical principles, illustrating the power of multiplication, the commutative and associative properties, and the connections between various mathematical fields. Its practical applications extend to various aspects of everyday life, from shopping to advanced scientific calculations. By mastering the fundamentals, we build a strong foundation for tackling more complex mathematical challenges and appreciating the beauty and power of mathematics in its entirety. Remember, even the most complex equations are built upon these foundational principles, making the understanding of basic arithmetic operations like multiplication essential for mathematical growth.
Latest Posts
Latest Posts
-
Ghana Vrs Mali
Sep 25, 2025
-
40 Of 34
Sep 25, 2025
-
Sentence With Epitome
Sep 25, 2025
-
Psi To Psia
Sep 25, 2025
-
Chairs For Disabled
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3 2x 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.