X 4 81
interactiveleap
Sep 21, 2025 · 5 min read
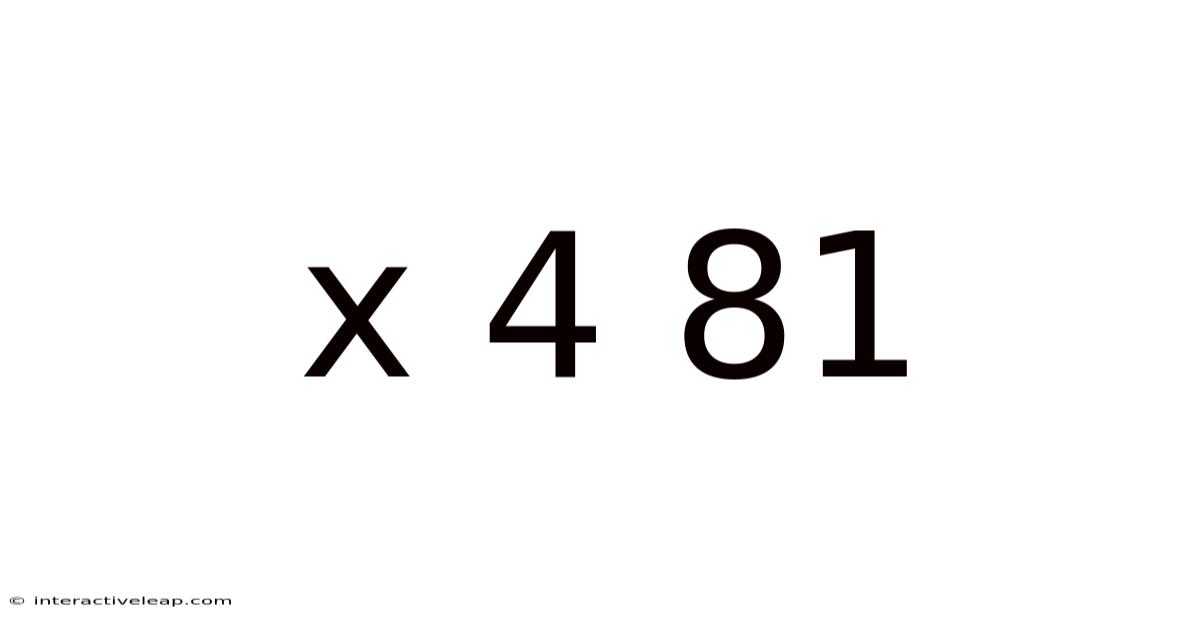
Table of Contents
Decoding x⁴ + 81: A Deep Dive into Polynomial Factorization and Complex Numbers
This article explores the fascinating factorization of the polynomial x⁴ + 81. While seemingly simple at first glance, this expression reveals a rich tapestry of mathematical concepts, including complex numbers, the difference of squares, and the sum of cubes. We will unravel its solution step-by-step, explaining the underlying principles in a clear and accessible manner, suitable for students and enthusiasts alike. Understanding this factorization provides valuable insight into advanced algebraic techniques and the beauty of mathematical structure.
Introduction: The Challenge of x⁴ + 81
At first glance, x⁴ + 81 might appear unfactorable using standard real number techniques. There are no obvious common factors, and it doesn't fit the familiar forms of quadratic or cubic factorization. However, by venturing into the realm of complex numbers, we can elegantly decompose this expression into its constituent factors. This journey will demonstrate the power and utility of complex numbers in solving seemingly intractable problems.
Stepping Stones: The Difference of Squares and the Sum of Cubes
Before tackling x⁴ + 81 directly, let's review two fundamental factorization identities that will prove crucial:
- Difference of Squares: a² - b² = (a + b)(a - b)
- Sum of Cubes: a³ + b³ = (a + b)(a² - ab + b²)
These identities are fundamental tools in algebraic manipulation. Our approach to factoring x⁴ + 81 will cleverly leverage these identities through a series of strategic substitutions and manipulations.
Factorization Strategy: Introducing Complex Numbers
The key to unlocking the factorization of x⁴ + 81 lies in recognizing that we can rewrite the expression as a difference of squares, albeit using complex numbers. Recall that i (iota) represents the imaginary unit, where i² = -1.
Let's rewrite x⁴ + 81 as:
(x²)² - (9i²)²
Notice that we've cleverly introduced the imaginary unit, i, to transform the problem into a difference of squares. Now we can apply the difference of squares formula:
(x²)² - (9i²)² = (x² + 9i²)(x² - 9i²)
Further simplification is possible. Remember that i² = -1, so we can substitute:
(x² - 9)(x² + 9)
This is a significant step, but we're not quite finished. We can factor the second term further using the difference of squares again:
x² - 9 = (x - 3)(x + 3)
However, the term x² + 9 cannot be factored further using only real numbers. To proceed, we must again use complex numbers. We can rewrite x² + 9 as:
x² - (3i)²
And apply the difference of squares:
x² - (3i)² = (x - 3i)(x + 3i)
The Complete Factorization of x⁴ + 81
Combining all our steps, the complete factorization of x⁴ + 81 using complex numbers is:
x⁴ + 81 = (x - 3)(x + 3)(x - 3i)(x + 3i)
Understanding the Complex Roots
The factorization reveals four roots for the equation x⁴ + 81 = 0:
- x = 3
- x = -3
- x = 3i
- x = -3i
These roots are a mixture of real and complex numbers. The real roots (3 and -3) are easily visualized on the number line. The complex roots (3i and -3i) lie on the imaginary axis of the complex plane.
Visualizing the Roots in the Complex Plane
The four roots of x⁴ + 81 = 0 are symmetrically arranged in the complex plane. They form a square with vertices at 3, -3, 3i, and -3i. This symmetrical arrangement is a characteristic feature of polynomial equations with complex roots. This visualization highlights the geometric interpretation of complex numbers and their connection to polynomial equations.
The Significance of Complex Numbers in Polynomial Factorization
This example beautifully illustrates the importance of extending our mathematical toolkit beyond real numbers. Many polynomial equations, particularly those of higher degree, possess complex roots. The inclusion of complex numbers allows us to obtain a complete factorization, providing a more comprehensive understanding of the polynomial's behavior and properties.
Applications and Further Exploration
The factorization of x⁴ + 81 and its underlying principles have applications in various areas of mathematics and related fields:
- Abstract Algebra: The factorization demonstrates the properties of polynomial rings and their ideals.
- Signal Processing: Complex numbers are fundamental in representing and analyzing signals.
- Quantum Mechanics: Complex numbers play a crucial role in the mathematical formulation of quantum mechanics.
- Electrical Engineering: Complex numbers are used extensively in circuit analysis and signal processing.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to use complex numbers in this factorization?
A: Using only real numbers, we cannot fully factor x² + 9. The introduction of complex numbers allows us to express this term as a difference of squares, enabling a complete factorization.
-
Q: Can this method be applied to other polynomials of the form xⁿ + aⁿ?
A: Similar techniques can be employed for other polynomials of the form xⁿ + aⁿ, particularly when n is an even number. However, the complexity of the factorization increases with the degree of the polynomial.
-
Q: What are the implications of the complex roots for the graph of y = x⁴ + 81?
A: The graph of y = x⁴ + 81 will not intersect the x-axis at the complex roots. The real roots (x = 3 and x = -3) represent the points where the graph intersects the x-axis.
Conclusion: A Journey into the World of Complex Numbers
The factorization of x⁴ + 81, although seemingly a simple algebraic problem, serves as a powerful illustration of the elegance and utility of complex numbers. By extending our mathematical framework beyond the real numbers, we've gained the ability to fully factor a polynomial that initially seemed intractable. This journey highlights the interconnectedness of various mathematical concepts and the surprising power of seemingly abstract mathematical tools. The beauty of mathematics lies not only in its practical applications but also in the intellectual satisfaction of unraveling intricate problems and discovering deeper underlying structures. The exploration of x⁴ + 81 provides a perfect entry point into this fascinating world.
Latest Posts
Latest Posts
-
After Dark Meaning
Sep 22, 2025
-
0 07 As Fraction
Sep 22, 2025
-
N Type Battery
Sep 22, 2025
-
Technical Advice Memorandum
Sep 22, 2025
-
45 Of 240
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X 4 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.