45 Of 240
interactiveleap
Sep 22, 2025 · 5 min read
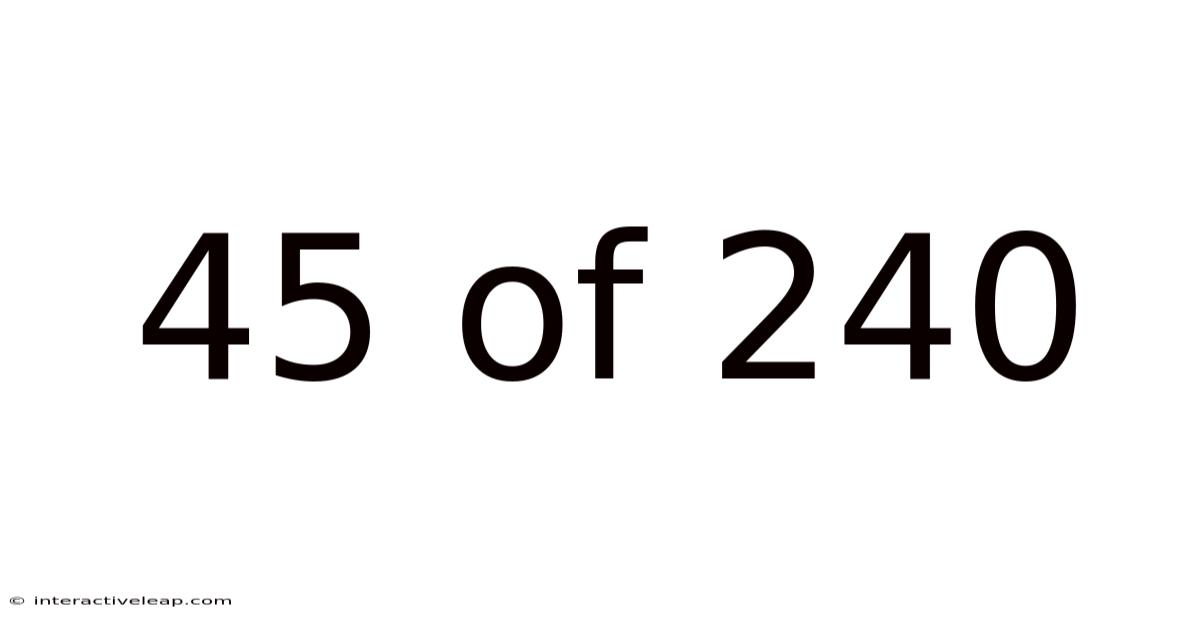
Table of Contents
Decoding the Fraction: Unveiling the Meaning and Applications of 45/240
Understanding fractions can seem daunting, especially when dealing with larger numbers. This article delves deep into the fraction 45/240, exploring its simplification, practical applications, and the underlying mathematical concepts. We’ll uncover its true value and demonstrate how seemingly complex fractions can be broken down into manageable and insightful pieces. This guide is perfect for students, educators, or anyone looking to solidify their understanding of fractions and their real-world significance.
Introduction: Understanding the Basics of Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered. In our case, 45/240 means 45 parts out of a total of 240 equal parts.
Before we dive into the specifics of 45/240, let's refresh some key concepts:
-
Simplifying Fractions: This involves reducing the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. This doesn't change the value of the fraction, only its representation.
-
Equivalent Fractions: These are fractions that represent the same value, even though they have different numerators and denominators. For example, 1/2, 2/4, and 3/6 are all equivalent fractions.
-
Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to its denominator (e.g., 7/4). A mixed number combines a whole number and a proper fraction (e.g., 1 ¾).
Simplifying 45/240: Finding the Greatest Common Divisor (GCD)
The first step in working with 45/240 is simplification. To do this, we need to find the GCD of 45 and 240. There are several methods to find the GCD:
-
Prime Factorization: This involves breaking down each number into its prime factors.
- 45 = 3 x 3 x 5 = 3² x 5
- 240 = 2 x 2 x 2 x 2 x 3 x 5 = 2⁴ x 3 x 5
The GCD is the product of the common prime factors raised to the lowest power. In this case, the common factors are 3 and 5, both raised to the power of 1. Therefore, the GCD(45, 240) = 3 x 5 = 15.
-
Euclidean Algorithm: This is an iterative method that involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- 240 ÷ 45 = 5 with a remainder of 15
- 45 ÷ 15 = 3 with a remainder of 0
The GCD is 15.
Now that we have the GCD, we can simplify the fraction:
45 ÷ 15 = 3 240 ÷ 15 = 16
Therefore, 45/240 simplifies to 3/16. This simplified fraction is much easier to work with and understand.
Representing 3/16: Visualizations and Interpretations
The simplified fraction 3/16 can be visualized in several ways:
-
As a part of a whole: Imagine a pizza cut into 16 equal slices. 3/16 represents 3 of those slices.
-
As a decimal: To convert 3/16 to a decimal, divide the numerator (3) by the denominator (16): 3 ÷ 16 = 0.1875.
-
As a percentage: Multiply the decimal by 100: 0.1875 x 100 = 18.75%. So, 3/16 represents 18.75% of the whole.
Real-World Applications of 45/240 (or 3/16)
Fractions like 45/240, and its simplified form 3/16, appear in various real-world scenarios:
-
Measurement and Proportion: Imagine you're mixing a paint solution. If the recipe calls for 45ml of pigment in a 240ml solution, simplifying to 3/16 helps visualize the pigment-to-solution ratio.
-
Probability and Statistics: If you have a bag with 240 marbles, 45 of which are red, the probability of picking a red marble is 45/240, or 3/16.
-
Data Analysis: When analyzing data sets, ratios often emerge as fractions. Simplifying these fractions provides a clearer understanding of the proportions involved.
-
Engineering and Construction: Accurate measurements and calculations are critical in these fields, and fractions are frequently used to express precise proportions and dimensions.
Further Exploration: Working with Fractions
Beyond simplification, several other operations can be performed with fractions:
-
Addition and Subtraction: To add or subtract fractions, they must have a common denominator. If they don't, you need to find the least common multiple (LCM) of the denominators and convert the fractions to equivalent fractions with the LCM as the denominator.
-
Multiplication: Multiplying fractions is relatively straightforward. You multiply the numerators together and the denominators together.
-
Division: To divide fractions, you invert the second fraction (reciprocal) and then multiply.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 45/240?
A: The simplest form of 45/240 is 3/16.
Q: How do I convert 45/240 to a decimal?
A: First simplify to 3/16, then divide 3 by 16 to get 0.1875.
Q: What percentage is 45/240?
A: 45/240 is equivalent to 18.75%.
Q: Can I use a calculator to simplify fractions?
A: Yes, many calculators have a function to simplify fractions. However, understanding the underlying mathematical concepts (like finding the GCD) is crucial for a deeper understanding.
Q: Are there other methods besides prime factorization and the Euclidean algorithm to find the GCD?
A: Yes, there are other algorithms, but these two are commonly used and relatively straightforward.
Conclusion: Mastering Fractions – A Building Block for Mathematical Proficiency
Understanding fractions is a fundamental skill in mathematics and has widespread applications in various fields. While initially seeming complex, fractions become manageable with practice and a solid grasp of the underlying principles. The example of 45/240, simplified to the more manageable 3/16, highlights the importance of simplification and visualization in comprehending fractional values. By mastering these concepts, you'll build a strong foundation for more advanced mathematical concepts and problem-solving. Remember that practice is key – continue working with different fractions to solidify your understanding and build confidence in your abilities. The seemingly daunting world of fractions will become a familiar and manageable landscape with dedicated effort.
Latest Posts
Latest Posts
-
102cm In Feet
Sep 22, 2025
-
280ml In Oz
Sep 22, 2025
-
15 Off 36
Sep 22, 2025
-
Female Crown Tattoos
Sep 22, 2025
-
200mins In Hours
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 45 Of 240 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.