X 2 4x
interactiveleap
Sep 15, 2025 · 6 min read
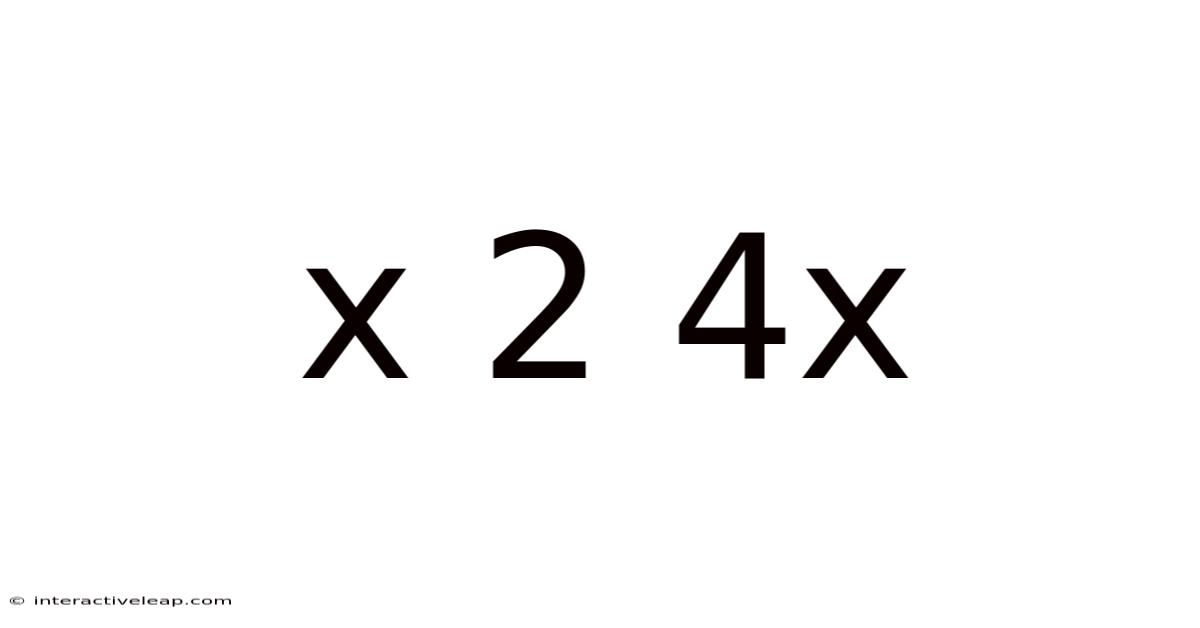
Table of Contents
Decoding the Mystery: A Deep Dive into x² + 4x
The expression x² + 4x is a fundamental concept in algebra, appearing frequently in various mathematical contexts. Understanding this seemingly simple expression unlocks doors to solving quadratic equations, graphing parabolas, and comprehending more complex mathematical concepts. This comprehensive guide will dissect x² + 4x, exploring its various facets from basic manipulation to advanced applications. We'll cover everything from simplifying the expression to completing the square, factoring, and even its graphical representation. By the end, you'll have a solid grasp of this crucial algebraic building block.
Understanding the Basics: Terms and Components
Before delving into the complexities, let's lay the groundwork. The expression x² + 4x is a polynomial—specifically, a quadratic polynomial because the highest power of the variable x is 2. It consists of two terms:
-
x²: This term is a quadratic term. It represents x multiplied by itself (x * x). The coefficient (the number in front of the variable) is implicitly 1.
-
4x: This term is a linear term. It represents 4 multiplied by x. The coefficient is 4.
Understanding these terms is crucial for performing operations on the expression.
Simplifying and Factoring the Expression
Often, the first step in working with x² + 4x is to simplify or factor it. Simplification usually involves combining like terms (which we don't have in this case, as there are only two unique terms), while factoring involves expressing the expression as a product of simpler expressions.
While x² + 4x cannot be simplified further, it can be factored. This involves finding two expressions whose product is x² + 4x. We can achieve this using a technique called factoring out the greatest common factor (GCF). In this case, the GCF is x:
x² + 4x = x(x + 4)
This factored form reveals that the expression is the product of x and (x + 4). This factored form is incredibly useful in solving equations and other algebraic manipulations.
Completing the Square: A Powerful Technique
Completing the square is a technique used to transform a quadratic expression into a perfect square trinomial, plus a constant term. This method is particularly useful when solving quadratic equations and understanding the graphical representation of the quadratic function.
To complete the square for x² + 4x, we follow these steps:
-
Take half of the coefficient of the linear term (4x): Half of 4 is 2.
-
Square the result: 2² = 4
-
Add and subtract this value to the original expression:
x² + 4x + 4 - 4
-
Group the first three terms to form a perfect square trinomial:
(x² + 4x + 4) - 4
-
Factor the perfect square trinomial:
(x + 2)² - 4
Therefore, completing the square transforms x² + 4x into (x + 2)² - 4. This form is valuable because it directly reveals the vertex of the parabola representing the quadratic function (more on this in the next section).
Graphical Representation: Visualizing the Parabola
The expression x² + 4x represents a quadratic function, which when graphed, produces a parabola. The completed square form, (x + 2)² - 4, makes it easy to identify key features of this parabola:
-
Vertex: The vertex of the parabola is the point (-2, -4). The completed square form directly shows the x-coordinate of the vertex as -2 (from (x + 2)²), and substituting this value into the original expression gives the y-coordinate as -4.
-
Axis of Symmetry: The axis of symmetry is a vertical line that passes through the vertex. Its equation is x = -2.
-
Concavity: Since the coefficient of the x² term (which is 1) is positive, the parabola opens upwards.
Understanding these features allows us to sketch the parabola accurately. The parabola will be a U-shaped curve, with its lowest point at the vertex (-2, -4) and opening upwards. The x-intercepts (where the parabola intersects the x-axis) can be found by setting the expression equal to zero and solving for x:
x² + 4x = 0 x(x + 4) = 0 x = 0 or x = -4
Thus, the parabola intersects the x-axis at (0, 0) and (-4, 0).
Solving Quadratic Equations: Applications of x² + 4x
The expression x² + 4x often arises when solving quadratic equations. A quadratic equation is an equation of the form ax² + bx + c = 0, where a, b, and c are constants and a ≠ 0. In our case, we might have an equation like:
x² + 4x = 0
or a more complex equation that simplifies to this form. We can solve this equation using several methods:
-
Factoring: As shown earlier, x² + 4x can be factored into x(x + 4) = 0. This implies that x = 0 or x = -4.
-
Quadratic Formula: The quadratic formula provides a general solution for any quadratic equation:
x = [-b ± √(b² - 4ac)] / 2a
For the equation x² + 4x = 0 (where a = 1, b = 4, c = 0), the quadratic formula yields the same solutions: x = 0 and x = -4.
-
Completing the Square: Completing the square, as demonstrated previously, transforms the equation into a solvable form:
(x + 2)² - 4 = 0 (x + 2)² = 4 x + 2 = ±2 x = 0 or x = -4
Extending the Concepts: Beyond the Basics
The understanding of x² + 4x lays the foundation for more advanced mathematical concepts:
-
Calculus: The derivative of x² + 4x is 2x + 4, which represents the instantaneous rate of change of the function. The integral is (1/3)x³ + 2x² + C, where C is the constant of integration. These concepts are crucial in understanding the behavior of the function and its applications in physics, engineering, and other fields.
-
Linear Algebra: Quadratic forms, which are generalizations of quadratic expressions like x² + 4x, play a significant role in linear algebra. They're used in various applications, including optimization problems and the analysis of conic sections.
-
Complex Numbers: The solutions to quadratic equations might involve complex numbers if the discriminant (b² - 4ac) is negative. While x² + 4x has real solutions, understanding the context of complex numbers expands the applicability of quadratic equations.
Frequently Asked Questions (FAQ)
Q: What is the difference between x² and 4x?
A: x² represents x multiplied by itself (x*x), while 4x represents 4 multiplied by x. x² is a quadratic term, and 4x is a linear term.
Q: Can x² + 4x be simplified further?
A: No, x² + 4x cannot be simplified further because the terms are not like terms (they don't have the same variable raised to the same power).
Q: What does it mean to factor an expression?
A: Factoring an expression means to rewrite it as a product of simpler expressions. For instance, factoring x² + 4x results in x(x + 4).
Q: What is the purpose of completing the square?
A: Completing the square is a technique used to transform a quadratic expression into a perfect square trinomial plus a constant. This form reveals the vertex of the parabola and simplifies solving quadratic equations.
Q: How can I find the x-intercepts of the parabola represented by x² + 4x?
A: To find the x-intercepts, set the expression equal to zero (x² + 4x = 0) and solve for x. This can be done by factoring or using the quadratic formula.
Conclusion: Mastering the Fundamentals
The seemingly simple expression x² + 4x is a gateway to a wealth of mathematical knowledge. Understanding its properties, manipulations, and graphical representation unlocks a deeper comprehension of quadratic equations, parabolas, and more advanced mathematical concepts. By mastering the techniques of factoring, completing the square, and applying the quadratic formula, you’ll solidify your foundation in algebra and prepare yourself for more complex mathematical challenges. Remember that consistent practice and a curious mind are key to unlocking the full potential of this foundational algebraic expression.
Latest Posts
Latest Posts
-
2x 7 13
Sep 16, 2025
-
180 X 12
Sep 16, 2025
-
70000 12
Sep 16, 2025
-
Rigger Meaning Bdsm
Sep 16, 2025
-
Humour And Irony
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 2 4x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.