X 15 9
interactiveleap
Sep 21, 2025 · 6 min read
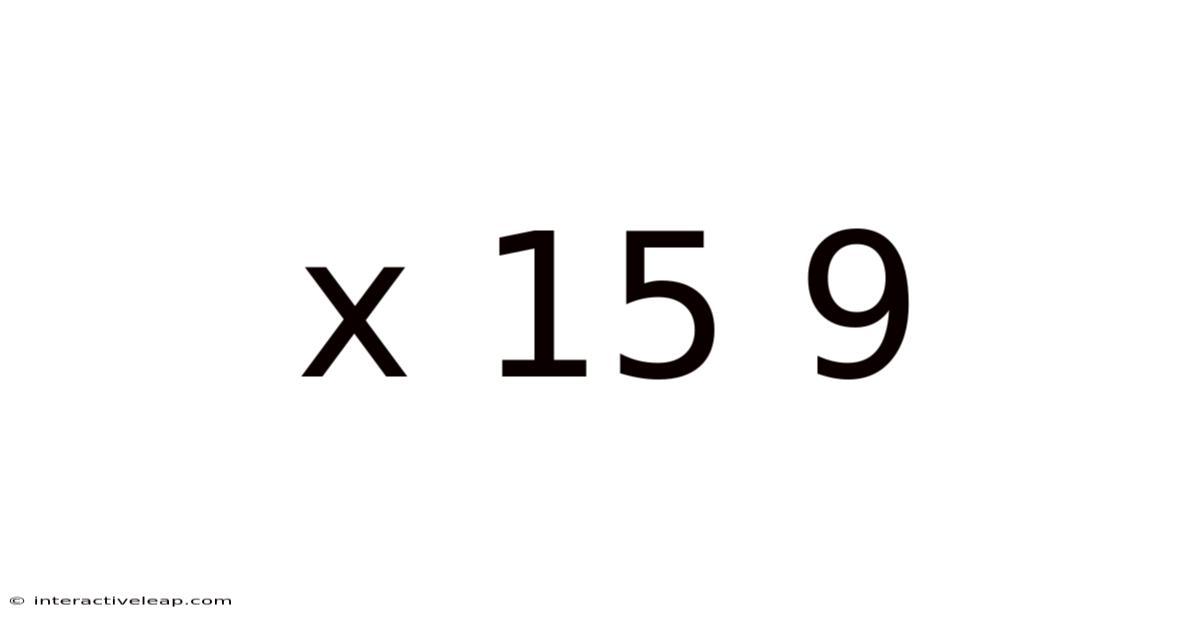
Table of Contents
Unraveling the Mystery of X x 15 = 9: A Deep Dive into Mathematical Concepts
This article delves into the intriguing mathematical puzzle represented by "x * 15 = 9," exploring its solution, the underlying concepts, and its implications within broader mathematical frameworks. We will unpack the process of solving for 'x', discuss the significance of algebraic manipulation, and consider the application of this simple equation to more complex problems. This seemingly basic equation opens the door to understanding fundamental principles crucial for higher-level mathematics. The keyword "algebraic equations" and related terms will be naturally integrated throughout the discussion.
Understanding the Equation: A Beginner's Guide
At its core, "x * 15 = 9" is a simple algebraic equation. An algebraic equation involves one or more variables (represented by letters like 'x') and constants (numbers like 15 and 9), connected by mathematical operations (in this case, multiplication and equality). The goal is to find the value of the unknown variable ('x') that makes the equation true. This equation specifically illustrates a linear equation because the variable 'x' is raised to the power of 1 (it's not squared, cubed, or raised to any other power).
The equation states that an unknown number ('x') multiplied by 15 equals 9. Our task is to isolate 'x' on one side of the equation to determine its value. This process involves using the principles of inverse operations.
Solving for 'x': Step-by-Step Solution
To solve for 'x', we employ the inverse operation of multiplication, which is division. Since 'x' is multiplied by 15, we divide both sides of the equation by 15 to isolate 'x':
x * 15 = 9
x * 15 / 15 = 9 / 15
x = 9/15
This fraction can be simplified by finding the greatest common divisor (GCD) of 9 and 15, which is 3. Dividing both the numerator and denominator by 3 gives us the simplified fraction:
x = 3/5
Therefore, the solution to the equation x * 15 = 9 is x = 3/5 or x = 0.6. This means that if you multiply 3/5 (or 0.6) by 15, the result will be 9.
Beyond the Solution: Understanding the Broader Mathematical Context
While solving for 'x' provides a numerical answer, it's crucial to understand the underlying mathematical principles at play. This seemingly simple equation introduces several fundamental concepts:
-
Variables and Constants: The equation highlights the distinction between variables (unknown values represented by letters) and constants (known numerical values). This distinction is crucial in all algebraic manipulations.
-
Inverse Operations: The solution process demonstrates the use of inverse operations. Multiplication and division are inverse operations; addition and subtraction are also inverse operations. Understanding inverse operations is essential for solving various types of equations.
-
Fractions and Decimals: The solution is expressed as both a fraction (3/5) and a decimal (0.6). This illustrates the equivalence between different numerical representations. Working comfortably with fractions and decimals is vital for many mathematical applications.
-
Equality and Balance: The equals sign (=) signifies equality. Any operation performed on one side of the equation must also be performed on the other side to maintain the balance and ensure the equality remains true. This concept is foundational to solving any equation.
-
Simplification and Reduction: Simplifying the fraction 9/15 to 3/5 demonstrates the importance of presenting solutions in their simplest form. This improves clarity and understanding.
Applying the Concepts: Expanding to More Complex Equations
The principles learned from solving "x * 15 = 9" are directly applicable to more complex algebraic equations. Consider the following examples:
-
Solving for x in 2x + 5 = 11: This equation involves both multiplication and addition. First, subtract 5 from both sides, then divide by 2 to isolate 'x'.
-
Solving for y in 3y - 7 = 14: Similar to the previous example, this equation utilizes inverse operations to solve for the unknown variable.
-
Solving systems of equations: More advanced problems might involve multiple equations with multiple unknowns, requiring techniques like substitution or elimination to find the solution. The fundamental principles of solving linear equations remain crucial in these scenarios.
The ability to solve simple algebraic equations like "x * 15 = 9" forms the bedrock for tackling increasingly complex mathematical problems in various fields.
The Importance of Algebraic Manipulation in Real-World Applications
Algebraic equations are not confined to textbooks and classrooms. They are essential tools across numerous fields:
-
Engineering: Engineers use algebraic equations extensively in designing structures, circuits, and systems. Calculating forces, stresses, currents, and voltages often relies on solving equations.
-
Physics: Many physical laws and phenomena are described by mathematical equations. Solving these equations is essential for understanding and predicting physical behavior.
-
Computer Science: Programming and algorithm development frequently involve solving equations to handle data, control program flow, and manage computational processes.
-
Finance: Financial modeling and forecasting often involve solving complex equations to analyze investment strategies, predict market trends, and manage risk.
-
Economics: Economic models rely heavily on algebraic equations to represent relationships between economic variables. Understanding these equations is vital for analyzing economic trends and making policy decisions.
Frequently Asked Questions (FAQ)
Q1: What if the equation was x / 15 = 9? How would I solve it?
A1: In this case, the inverse operation would be multiplication. Multiply both sides of the equation by 15 to isolate x: x = 9 * 15 = 135.
Q2: Can this equation have more than one solution?
A2: No, linear equations like this one have only one solution. There's only one value of 'x' that satisfies the equation.
Q3: What if the numbers were different? Would the solving process change?
A3: The process would remain the same. You would still use inverse operations to isolate the variable. The specific numbers would affect the numerical solution, but the fundamental approach remains consistent.
Q4: What are some common mistakes students make when solving this type of equation?
A4: Common mistakes include forgetting to perform the same operation on both sides of the equation, incorrectly applying inverse operations, and making errors in arithmetic calculations (especially when dealing with fractions or decimals). Careful attention to detail is crucial.
Conclusion: Mastering the Fundamentals
The seemingly simple equation "x * 15 = 9" provides a gateway to understanding fundamental concepts within algebra. Mastering the process of solving for 'x' is not just about obtaining a numerical answer; it's about grasping the principles of inverse operations, variable manipulation, and maintaining equation balance. These principles form the cornerstone for tackling more complex mathematical challenges and are applicable across diverse fields, underscoring the equation's significance far beyond its apparent simplicity. By understanding the solution and its underlying principles, we unlock a deeper appreciation for the power and elegance of algebra. The ability to confidently solve such equations lays a solid foundation for future mathematical endeavors and real-world applications.
Latest Posts
Latest Posts
-
0 25 To Percentage
Sep 21, 2025
-
14kg In Lb
Sep 21, 2025
-
16 1 2
Sep 21, 2025
-
124lbs To Kg
Sep 21, 2025
-
110 30 Off
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about X 15 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.