0.25 To Percentage
interactiveleap
Sep 21, 2025 · 5 min read
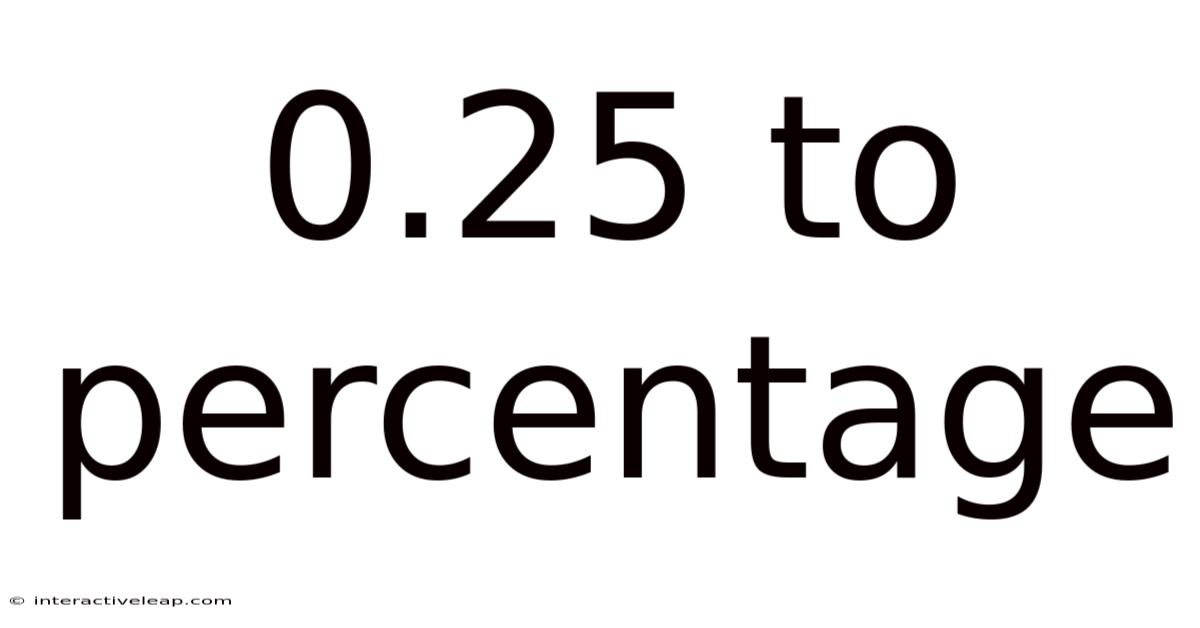
Table of Contents
Converting 0.25 to a Percentage: A Comprehensive Guide
Understanding how to convert decimals to percentages is a fundamental skill in mathematics and has wide-ranging applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This comprehensive guide will walk you through the process of converting the decimal 0.25 to a percentage, explaining the underlying principles and providing practical examples to solidify your understanding. We will explore various methods, address common misconceptions, and delve into the broader context of decimal-to-percentage conversions.
Understanding Decimals and Percentages
Before diving into the conversion, let's briefly review the concepts of decimals and percentages. A decimal is a way of representing a number that is not a whole number. It uses a decimal point to separate the whole number part from the fractional part. For example, 0.25 represents a value that is less than 1.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion or rate per hundred. For instance, 25% means 25 parts out of 100, or 25/100. Both decimals and percentages are valuable tools for expressing parts of a whole.
Method 1: The Direct Multiplication Method
The most straightforward way to convert a decimal to a percentage is to multiply the decimal by 100. This is because a percentage is essentially a fraction with a denominator of 100.
To convert 0.25 to a percentage, we perform the following calculation:
0.25 * 100 = 25
Therefore, 0.25 is equivalent to 25%.
This method is based on the fundamental relationship between decimals and percentages. Multiplying by 100 effectively shifts the decimal point two places to the right.
Method 2: The Fractional Method
Alternatively, we can convert the decimal to a fraction and then express it as a percentage. The decimal 0.25 can be written as the fraction 25/100. Since a percentage is a fraction out of 100, this fraction is already in the desired form.
25/100 = 25%
This method highlights the inherent connection between decimals, fractions, and percentages. It reinforces the understanding that a percentage is simply a specific type of fraction.
Method 3: Using Proportions
We can also approach this conversion using proportions. We can set up a proportion where the decimal 0.25 is equivalent to 'x' percent out of 100.
0.25 / 1 = x / 100
To solve for x, we cross-multiply:
1 * x = 0.25 * 100 x = 25
Therefore, 0.25 is equal to 25%. This method demonstrates the proportional relationship between decimals and percentages.
Visual Representation: Understanding the Concept
Imagine a 100-square grid. If you shade 25 squares, you have shaded 25% of the grid. This visual representation directly links the concept of percentage to the decimal value of 0.25. Each square represents 1%, and 25 squares represent 25%. This visual method helps to internalize the meaning of the conversion.
Real-World Applications of Decimal-to-Percentage Conversions
The ability to convert decimals to percentages is crucial in numerous real-world scenarios:
-
Sales and Discounts: A store offering a 25% discount on an item is essentially reducing the price by 0.25 times the original price.
-
Taxes: Sales taxes are often expressed as percentages. Understanding this conversion helps to calculate the final price of goods and services.
-
Financial Statements: Financial reports frequently utilize percentages to represent various ratios and key performance indicators (KPIs), such as profit margins and return on investment (ROI).
-
Statistics: Percentages are widely used in statistical analysis to represent proportions, probabilities, and frequencies. Converting decimals from statistical calculations to percentages makes the data more easily interpretable.
-
Scientific Data: In various scientific fields, experimental data is often expressed as decimals, and converting them to percentages provides a more intuitive understanding of the results.
Addressing Common Misconceptions
One common misunderstanding is the belief that simply adding a percentage sign to a decimal automatically converts it to a percentage. This is incorrect. The multiplication by 100 is a necessary step to accurately represent the value as a percentage.
Beyond 0.25: Converting Other Decimals to Percentages
The methods described above can be applied to convert any decimal to a percentage. For example:
- 0.50 = 0.50 * 100 = 50%
- 0.75 = 0.75 * 100 = 75%
- 0.10 = 0.10 * 100 = 10%
- 1.00 = 1.00 * 100 = 100%
- 0.05 = 0.05 * 100 = 5%
Converting Percentages Back to Decimals
The reverse process is equally important. To convert a percentage back to a decimal, divide the percentage by 100. For example, to convert 25% back to a decimal:
25% / 100 = 0.25
Frequently Asked Questions (FAQ)
Q: What if the decimal has more than two decimal places?
A: The same principle applies. Multiply by 100, and the resulting number will be the percentage. For example, 0.255 * 100 = 25.5%, which is 25 and a half percent.
Q: Can I convert a fraction directly to a percentage without going through a decimal?
A: Yes, you can. Simply express the fraction with a denominator of 100 or convert it to an equivalent fraction with a denominator of 100, then the numerator will be the percentage. For example, 1/4 is equivalent to 25/100, so it represents 25%.
Q: Why is multiplying by 100 necessary for the conversion?
A: A percentage is a fraction out of 100. Multiplying the decimal by 100 expresses the value as a fraction with a denominator of 100, fulfilling the definition of a percentage.
Conclusion
Converting 0.25 to a percentage, resulting in 25%, is a simple yet fundamental concept with widespread applications. Understanding the underlying principles and the different methods presented in this guide will equip you with a valuable skill for navigating various mathematical and real-world situations. Whether you utilize the direct multiplication method, the fractional method, or the proportional method, the result remains consistent: 0.25 is equivalent to 25%, representing 25 parts out of 100. This knowledge empowers you to confidently interpret and utilize percentages in your daily life and across diverse fields of study and profession. Remember to practice these methods with various decimals to further solidify your understanding and build confidence in your ability to perform these essential conversions.
Latest Posts
Latest Posts
-
135 In Kilos
Sep 21, 2025
-
168lb In Kg
Sep 21, 2025
-
53 6kg In Stone
Sep 21, 2025
-
Crimson Deathcharger Mount
Sep 21, 2025
-
63 Divided 3
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 0.25 To Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.