Square Root 56.25
interactiveleap
Sep 23, 2025 · 5 min read
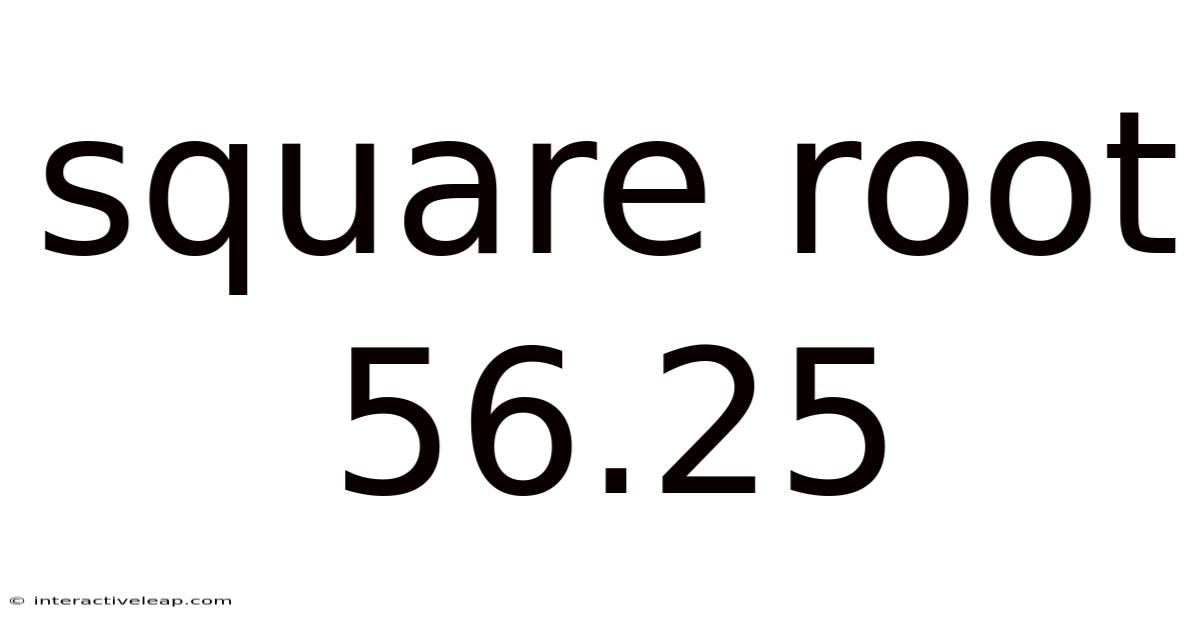
Table of Contents
Unveiling the Mystery: A Deep Dive into the Square Root of 56.25
Finding the square root of a number might seem like a simple mathematical operation, but understanding the underlying concepts and various methods for solving it can unlock a deeper appreciation for numbers and their relationships. This article delves into the intricacies of calculating the square root of 56.25, exploring different approaches, explaining the mathematical principles involved, and addressing frequently asked questions. We'll move beyond just the answer and explore the why behind the calculation, making this a valuable resource for students and anyone curious about the beauty of mathematics.
Understanding Square Roots: A Gentle Introduction
Before we tackle the specific problem of finding the square root of 56.25, let's establish a solid foundation. The square root of a number is a value that, when multiplied by itself, equals the original number. For instance, the square root of 9 is 3 because 3 x 3 = 9. This is often represented symbolically as √9 = 3. The square root operation is the inverse of squaring a number.
Square roots can be found for positive numbers, resulting in either positive or negative values (e.g., √25 = ±5 because both 5 x 5 and -5 x -5 equal 25). However, when dealing with the principal square root (often denoted by √), we generally focus on the positive value. This article will primarily focus on the positive principal square root.
Method 1: Prime Factorization and Simplification
One method to approach finding the square root of 56.25 involves converting the decimal to a fraction and then using prime factorization.
-
Convert to a Fraction: 56.25 can be expressed as the fraction 5625/100.
-
Simplify the Fraction: We can simplify this fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 25. This gives us 225/4.
-
Prime Factorization: Now, let's find the prime factorization of both the numerator and the denominator.
- 225 = 3 x 3 x 5 x 5 = 3² x 5²
- 4 = 2 x 2 = 2²
-
Rewrite the Fraction: Our simplified fraction becomes (3² x 5²) / 2².
-
Calculate the Square Root: Taking the square root of the fraction, we get:
√((3² x 5²) / 2²) = (√3² x √5²) / √2² = (3 x 5) / 2 = 15/2
-
Convert back to Decimal: Finally, converting the fraction back to a decimal, we get 7.5.
Therefore, the square root of 56.25 is 7.5.
Method 2: Utilizing the Properties of Squares
Another approach leverages our knowledge of perfect squares. We can try to find two numbers close to the square root of 56.25 and use estimation. We know that 7² = 49 and 8² = 64. Since 56.25 lies between these two squares, its square root must be between 7 and 8.
Let's try 7.5: 7.5 x 7.5 = 56.25. This confirms that our estimate was correct. This method is helpful for numbers that have easily identifiable square roots nearby.
Method 3: The Babylonian Method (or Heron's Method)
For numbers without easily recognizable square roots, iterative methods like the Babylonian method prove invaluable. This method involves repeatedly refining an initial guess until the desired accuracy is achieved.
-
Initial Guess: Start with an initial guess, let's say 7.
-
Iterative Refinement: The formula for the Babylonian method is:
x_(n+1) = (x_n + (N/x_n)) / 2
Where:
- x_n is the current guess
- x_(n+1) is the next guess
- N is the number whose square root we are seeking (56.25)
-
Iteration 1: x_1 = (7 + (56.25/7)) / 2 ≈ 7.5178
-
Iteration 2: x_2 = (7.5178 + (56.25/7.5178)) / 2 ≈ 7.5
As you can see, the method converges rapidly to 7.5. Further iterations would yield even more precise results, but the level of accuracy achieved after a couple of iterations is usually sufficient.
Method 4: Using a Calculator
The most straightforward method, especially for complex numbers, is employing a calculator or computer software. Most calculators have a dedicated square root function (√) which directly provides the result. Simply input 56.25 and press the square root button. The answer will be displayed as 7.5.
The Mathematical Explanation: Why Does it Work?
The success of these methods hinges on the fundamental properties of square roots and numbers. The prime factorization method leverages the fact that the square root of a product is the product of the square roots. The Babylonian method utilizes a geometric interpretation of the square root, converging towards the solution iteratively. Understanding these principles deepens your understanding of the mathematical underpinnings.
Frequently Asked Questions (FAQs)
-
Q: Can the square root of 56.25 be negative?
A: While mathematically, both 7.5 and -7.5 squared equal 56.25, the principal square root (the one typically denoted by √) is the positive value, 7.5.
-
Q: Are there any other methods to calculate square roots?
A: Yes, there are numerous other methods, including Newton-Raphson method (a generalization of the Babylonian method), and series expansions. However, the methods discussed above are generally sufficient for most practical purposes.
-
Q: What if the number is negative? Can I still find its square root?
A: The square root of a negative number involves imaginary numbers, specifically using the imaginary unit 'i', where i² = -1. For example, √(-9) = 3i. This is a topic explored in complex number theory.
-
Q: How accurate are these methods?
A: The accuracy depends on the method and the number of iterations (for iterative methods). Prime factorization and direct calculation using calculators offer precise results. The Babylonian method's accuracy increases with each iteration.
Conclusion: Beyond the Number
Calculating the square root of 56.25 is not just about getting the answer (7.5); it's about exploring different mathematical approaches and deepening your understanding of fundamental concepts. Whether you prefer the elegance of prime factorization, the iterative precision of the Babylonian method, or the simplicity of a calculator, each method offers a unique perspective on this seemingly simple operation. This exploration allows us to appreciate the interconnectedness of mathematical principles and the power of different problem-solving strategies. The journey of understanding the square root of 56.25 serves as a microcosm of the broader mathematical landscape – a landscape where seemingly simple problems reveal a wealth of underlying complexity and beauty.
Latest Posts
Latest Posts
-
2 5 X 10
Sep 23, 2025
-
1700kg Into Tonnes
Sep 23, 2025
-
You Wish Meaning
Sep 23, 2025
-
Bubble Tiny Mighties
Sep 23, 2025
-
Korean Eye Makeup
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Square Root 56.25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.