2.5 X 10
interactiveleap
Sep 23, 2025 · 6 min read
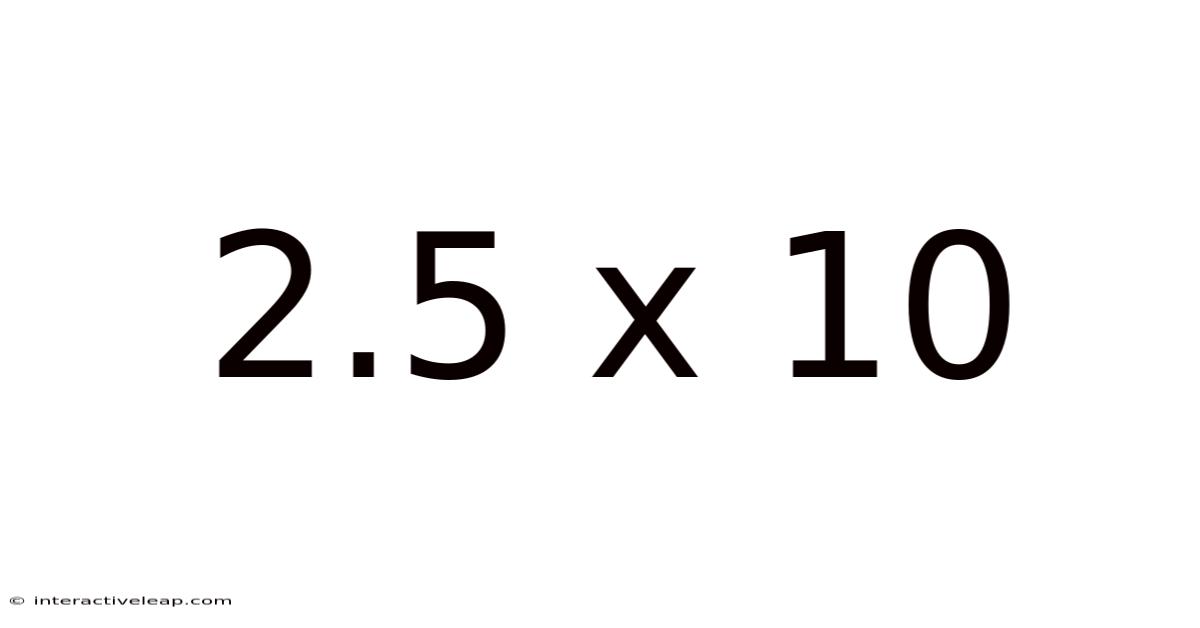
Table of Contents
Decoding 2.5 x 10: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 2.5 multiplied by 10, delving beyond the immediate answer to uncover the underlying mathematical principles and diverse applications across various fields. We'll examine the mechanics of decimal multiplication, explore different methods for solving the problem, and showcase real-world examples where this fundamental calculation plays a crucial role. Understanding 2.5 x 10 is not just about getting the right answer; it's about grasping a foundational concept that underpins more complex mathematical operations.
Understanding the Fundamentals: Decimal Multiplication
Before diving into the specifics of 2.5 x 10, let's refresh our understanding of decimal multiplication. Decimals represent fractions where the denominator is a power of 10 (e.g., 10, 100, 1000). Multiplying decimals involves the same principles as multiplying whole numbers, with the added step of handling the decimal point.
The key is to initially ignore the decimal point and multiply the numbers as if they were whole numbers. Then, count the total number of digits to the right of the decimal point in both numbers being multiplied. Finally, place the decimal point in the result so that the number of digits to the right of the decimal point equals the total count from the original numbers.
For instance, consider 2.5 x 10. If we ignore the decimal point, we have 25 x 10 = 250. Since there is only one digit to the right of the decimal point in 2.5 (the '5'), we place the decimal point in our result (250) one place from the right, resulting in 25.
Calculating 2.5 x 10: Different Approaches
There are several ways to calculate 2.5 x 10, each offering a slightly different perspective on the process.
-
Direct Multiplication: The most straightforward approach involves directly applying the decimal multiplication rule. As shown above, ignoring the decimal point gives us 25 x 10 = 250. With one digit to the right of the decimal point in 2.5, we move the decimal point one place to the left in 250, resulting in 25.
-
Fractional Representation: We can express 2.5 as the fraction 5/2. Therefore, 2.5 x 10 becomes (5/2) x 10. This simplifies to 50/2, which equals 25. This method highlights the relationship between decimals and fractions.
-
Distributive Property: We can break down 2.5 into 2 + 0.5. Using the distributive property of multiplication, we have: (2 + 0.5) x 10 = (2 x 10) + (0.5 x 10) = 20 + 5 = 25. This approach demonstrates the fundamental principle of breaking down complex calculations into simpler ones.
-
Multiplication by Powers of 10: Multiplying a number by a power of 10 (10, 100, 1000, etc.) is particularly easy. It simply involves moving the decimal point to the right by the number of zeros in the power of 10. In our case, multiplying 2.5 by 10 involves moving the decimal point one place to the right, giving us 25. This method showcases the efficiency of working with powers of 10.
Real-World Applications of 2.5 x 10
The seemingly simple calculation of 2.5 x 10 finds widespread application in various contexts:
-
Financial Calculations: Imagine calculating the total cost of 10 items priced at $2.50 each. The total cost is simply 2.5 x 10 = $25. This is a common scenario in everyday financial transactions.
-
Measurements and Conversions: If you have a piece of material 2.5 meters long and need 10 such pieces, the total length required is 2.5 x 10 = 25 meters. This is relevant in various fields like construction, tailoring, and engineering.
-
Data Analysis: In data analysis, consider a scenario where the average value of a certain variable is 2.5 units, and you have 10 data points. The total value of the variable across all 10 data points would be 2.5 x 10 = 25 units. Such calculations are common in statistics and data science.
-
Recipe Scaling: If a recipe calls for 2.5 cups of flour and you want to make 10 times the quantity, you will need 2.5 x 10 = 25 cups of flour. This principle is fundamental in cooking and baking.
-
Scientific Calculations: While not directly evident in many complex scientific formulas, the concept of multiplying decimals by powers of 10 underlies numerous calculations, often in units conversion or scaling experimental results.
Extending the Concept: Beyond 2.5 x 10
Understanding 2.5 x 10 provides a solid foundation for tackling more complex multiplication problems involving decimals and powers of 10. Consider the following extensions:
-
Multiplying by other powers of 10: The principles remain the same when multiplying by 100, 1000, or any other power of 10. The decimal point simply shifts to the right according to the number of zeros.
-
Multiplying by multiples of 10: Multiplying 2.5 by 20 (which is 2 x 10) can be broken down into (2.5 x 2) x 10 = 5 x 10 = 50. This illustrates the flexibility of combining multiplication rules.
-
Multiplying by decimals that are not powers of 10: Calculations like 2.5 x 3.2 require the standard decimal multiplication method, but the underlying principle of handling the decimal point remains the same.
-
Working with larger numbers: While the specific calculation 2.5 x 10 is relatively simple, the principles involved extend to calculations with much larger numbers. Understanding the fundamentals enables one to approach these more complex problems with confidence.
Frequently Asked Questions (FAQ)
-
Q: Why is multiplying by 10 so easy?
- A: Multiplying by 10 is equivalent to multiplying by 1 followed by a single zero. This is why it simply involves moving the decimal point one place to the right.
-
Q: What if I multiply 2.5 by 100?
- A: Multiplying 2.5 by 100 (which has two zeros) involves moving the decimal point two places to the right, resulting in 250.
-
Q: Can I use a calculator to solve 2.5 x 10?
- A: Yes, absolutely! Calculators are valuable tools for performing calculations quickly and accurately, especially when dealing with larger or more complex numbers. However, understanding the underlying mathematical principles is crucial for developing strong numerical reasoning skills.
-
Q: What if I have a number with multiple decimal places?
- A: The same principle applies: ignore the decimal point during the initial multiplication, then count the total number of digits to the right of the decimal point in both numbers and reposition the decimal point accordingly in the final answer.
-
Q: Is there a shortcut for multiplying decimals?
- A: While there isn't a universal shortcut for all decimal multiplications, understanding the principles of decimal multiplication and the strategies outlined above (like the distributive property or working with powers of 10) can significantly simplify the process for many common scenarios.
Conclusion: Mastering the Fundamentals
The seemingly straightforward calculation of 2.5 x 10 serves as a powerful example of the fundamental principles of multiplication and its applications across various domains. By understanding the different methods of solving this problem and exploring its real-world applications, we gain a deeper appreciation for the interconnectedness of mathematical concepts and their relevance in everyday life. Mastering this foundational calculation equips you not only to solve simple problems but also to tackle more complex mathematical challenges with confidence and efficiency. Remember that the key lies not only in obtaining the correct answer (25) but also in grasping the underlying principles, allowing you to apply these skills to a multitude of situations.
Latest Posts
Latest Posts
-
173lbs To Kg
Sep 23, 2025
-
5 5 Inches Mm
Sep 23, 2025
-
Technology During 1950s
Sep 23, 2025
-
75 Of 170
Sep 23, 2025
-
35 Of 180
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2.5 X 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.