Square Root 162
interactiveleap
Sep 21, 2025 · 5 min read
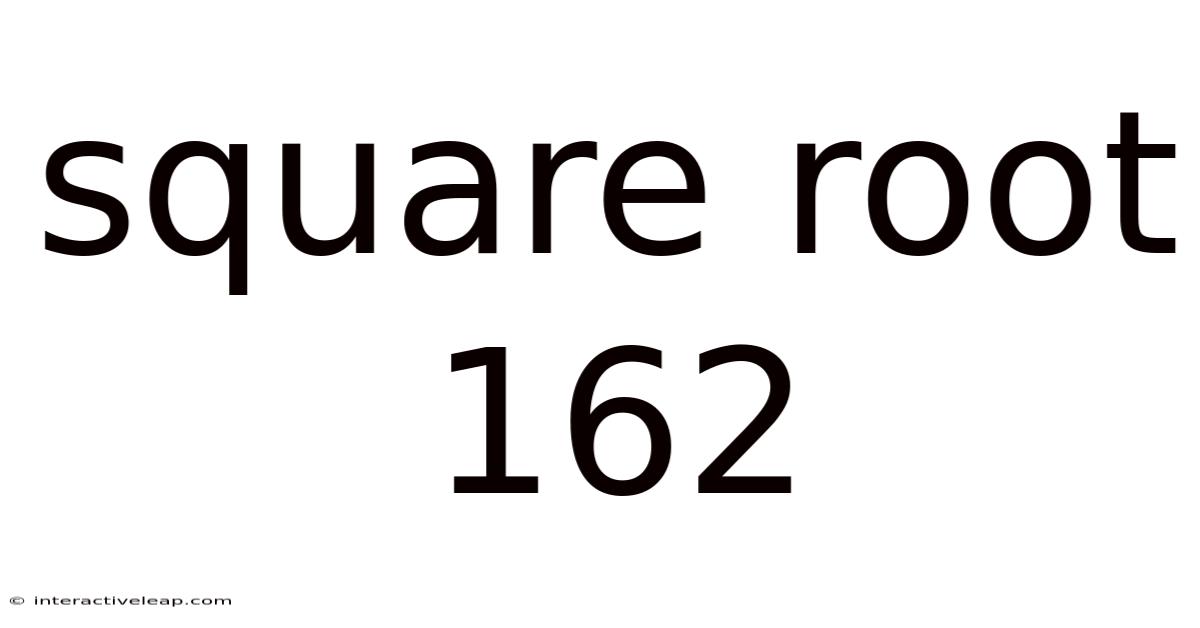
Table of Contents
Unveiling the Mysteries of the Square Root of 162: A Comprehensive Guide
Finding the square root of a number might seem like a simple mathematical operation, but understanding the process fully, especially with a number like 162, opens up a world of mathematical concepts. This article will delve deep into calculating the square root of 162, exploring different methods, explaining the underlying principles, and addressing frequently asked questions. We'll move beyond simply stating the answer and explore the rich mathematical landscape surrounding this seemingly straightforward problem.
Understanding Square Roots
Before we tackle the square root of 162, let's establish a firm understanding of what a square root actually is. The square root of a number (x) is another number (y) that, when multiplied by itself, equals x. In simpler terms: if y * y = x, then y is the square root of x. This is often written as √x = y. For example, the square root of 9 (√9) is 3 because 3 * 3 = 9.
However, not all numbers have perfect square roots – integers that result in whole numbers when squared. Numbers like 162 fall into this category. Their square roots are irrational numbers, meaning they cannot be expressed as a simple fraction and their decimal representation goes on forever without repeating.
Calculating the Square Root of 162: Methods and Approaches
There are several ways to approach calculating the square root of 162. Let's explore the most common ones:
1. Prime Factorization Method
This method is particularly useful for understanding the structure of the number and simplifying the square root. It involves breaking down 162 into its prime factors – numbers that are only divisible by 1 and themselves.
-
Find the prime factorization of 162: 162 = 2 x 81 = 2 x 9 x 9 = 2 x 3 x 3 x 3 x 3 = 2 x 3⁴
-
Simplify the square root: Since √(a * b) = √a * √b, we can rewrite √162 as: √(2 x 3⁴) = √2 x √(3⁴) = √2 x 3² = 9√2
Therefore, the simplified form of the square root of 162 is 9√2. This is often preferred as it’s a more precise representation than a decimal approximation.
2. Using a Calculator
The simplest approach is to use a calculator. Most scientific calculators have a square root function (√). Simply input 162 and press the square root button. The calculator will provide a decimal approximation, typically around 12.7279. However, keep in mind that this is only an approximation, as the true value is an irrational number.
3. The Babylonian Method (or Heron's Method)
This is an iterative method that provides increasingly accurate approximations of the square root. It's a powerful technique that showcases the iterative nature of many mathematical solutions.
The algorithm is as follows:
-
Make an initial guess: Let's start with a guess of 12.
-
Refine the guess: Divide 162 by the guess (162 / 12 = 13.5).
-
Average the guess and the result: (12 + 13.5) / 2 = 12.75
-
Repeat steps 2 and 3: 162 / 12.75 ≈ 12.7279; (12.75 + 12.7279) / 2 ≈ 12.7389
By repeating this process, the approximation will converge towards the actual square root of 162. The more iterations you perform, the more accurate the result will be. This method demonstrates a fundamental approach to solving problems numerically, highlighting the power of iterative algorithms in mathematics and computer science.
4. Long Division Method for Square Roots
This is a less common method but offers a deeper understanding of how the square root can be manually calculated without a calculator, particularly for perfect squares. It involves a step-by-step process similar to long division, but it's more complex and less efficient than the other methods for irrational numbers like √162.
Understanding the Irrationality of √162
As we've established, the square root of 162 is an irrational number. This means it cannot be expressed as a fraction of two integers. Its decimal representation is non-terminating and non-repeating. This seemingly simple fact highlights a fascinating aspect of mathematics: the existence of numbers that cannot be precisely represented using finite decimal places or fractions. The irrationality of √162 stems directly from the prime factorization; the presence of the prime factor 2, which cannot be paired, prevents a whole number result.
Applications of Square Roots
Understanding square roots is not just an academic exercise; it has practical applications across various fields:
-
Geometry: Calculating the lengths of sides and diagonals in squares, rectangles, and other geometric shapes frequently involves using square roots (e.g., Pythagorean theorem).
-
Physics: Many physics formulas, especially those involving distance, velocity, and acceleration, utilize square roots.
-
Engineering: Square roots are essential in various engineering calculations, such as structural analysis and electrical circuit design.
-
Computer graphics: Square roots are crucial in rendering and manipulating images in computer graphics.
Frequently Asked Questions (FAQ)
Q: What is the exact value of √162?
A: There is no exact decimal value for √162 as it is an irrational number. The most precise representation is 9√2.
Q: Why is 9√2 considered a simpler form than the decimal approximation?
A: 9√2 is considered simpler because it's an exact representation, avoiding the truncation or rounding errors inherent in decimal approximations. It also reveals the underlying mathematical structure of the number.
Q: Can I use a calculator for all square root calculations?
A: Calculators are convenient for approximating square roots, but understanding the underlying mathematical principles, like prime factorization, is crucial for a deeper grasp of the concept.
Q: Are there other methods to calculate square roots besides the ones mentioned?
A: Yes, several other methods exist, including more sophisticated numerical algorithms used in computers, but the ones described here offer a good starting point for understanding the fundamental concepts.
Conclusion
Calculating the square root of 162 is more than just plugging a number into a calculator. It's an opportunity to explore core mathematical concepts, from prime factorization and simplification to the nature of irrational numbers and iterative approximation techniques. Understanding these methods not only helps in solving this specific problem but also builds a stronger foundation for tackling more complex mathematical challenges across various disciplines. Remember, mastering mathematics is a journey, and every step, however seemingly small, contributes to a larger understanding. So, embrace the complexities, explore the different approaches, and let the mysteries of mathematics unfold before you.
Latest Posts
Latest Posts
-
179 Of 5800
Sep 21, 2025
-
Co2 Electron Geometry
Sep 21, 2025
-
25 Of 85
Sep 21, 2025
-
55 Of 80
Sep 21, 2025
-
600 X 7
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Square Root 162 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.