25 Of 85
interactiveleap
Sep 21, 2025 · 5 min read
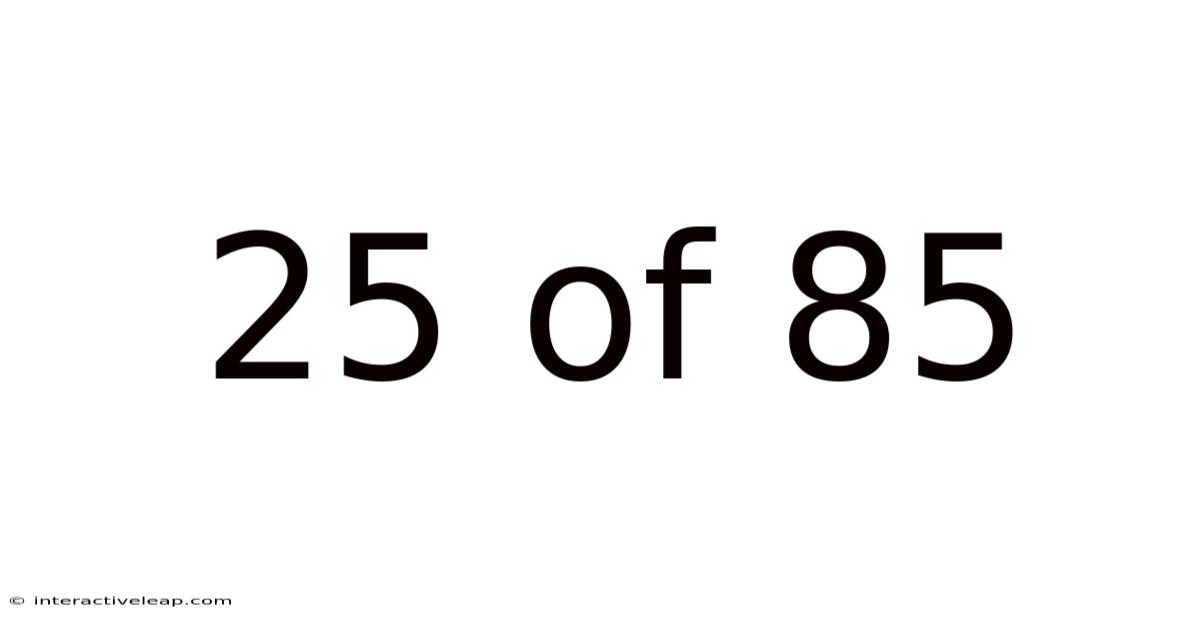
Table of Contents
Decoding the Mystery: Understanding 25 out of 85
Many of us encounter percentages and ratios daily, whether calculating discounts at the mall, assessing exam scores, or understanding statistics in the news. Sometimes, however, a simple fraction like "25 out of 85" can seem confusing, particularly when needing to translate it into a more easily understandable format, such as a percentage or a simplified fraction. This article delves into the meaning of "25 out of 85," exploring various ways to interpret and represent this fraction, providing practical examples, and clarifying common misconceptions. By the end, you'll be equipped to confidently handle similar fractional expressions and apply the concepts learned to real-world scenarios.
Understanding the Basics: Fractions and Ratios
Before diving into "25 out of 85," let's refresh our understanding of fundamental concepts. A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the part) and 'b' is the denominator (the whole). A ratio, on the other hand, compares two quantities. While similar to a fraction, ratios can compare parts of different wholes. In our case, "25 out of 85" can be interpreted both as a fraction (25/85) and a ratio (25:85), indicating that 25 is a part of a larger whole of 85.
Converting "25 out of 85" to a Percentage
Percentages are a convenient way to express fractions as a proportion of 100. To convert "25 out of 85" to a percentage, we follow these steps:
-
Express as a fraction: Write the expression as a fraction: 25/85.
-
Convert to a decimal: Divide the numerator (25) by the denominator (85): 25 ÷ 85 ≈ 0.2941
-
Multiply by 100: Multiply the decimal by 100 to express it as a percentage: 0.2941 × 100 ≈ 29.41%
Therefore, "25 out of 85" is approximately 29.41%. This means that 25 represents approximately 29.41% of the total 85.
Simplifying the Fraction: Finding the Lowest Terms
Simplifying a fraction involves reducing it to its lowest terms by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
-
Find the GCD of 25 and 85: The factors of 25 are 1, 5, and 25. The factors of 85 are 1, 5, 17, and 85. The greatest common factor is 5.
-
Divide both the numerator and the denominator by the GCD: Divide 25 by 5 and 85 by 5: 25/5 = 5 and 85/5 = 17.
Therefore, the simplified fraction is 5/17. This means that "25 out of 85" is equivalent to "5 out of 17." Both fractions represent the same proportion.
Real-World Applications: Illustrative Examples
Understanding "25 out of 85" isn't just about abstract mathematical concepts; it has practical applications in various real-world scenarios. Let's consider a few examples:
-
Exam Scores: Imagine a student scored 25 out of 85 on a test. Their score is approximately 29.41%, indicating they answered roughly 29% of the questions correctly. This provides a clear understanding of their performance relative to the total number of questions.
-
Sales Performance: A salesperson made 25 sales out of 85 potential clients. This translates to a success rate of approximately 29.41%, revealing their effectiveness in converting leads into sales. This data can inform strategies for improvement.
-
Survey Results: A survey of 85 people showed that 25 preferred a particular product. This represents roughly 29.41% of the respondents, providing valuable market research data. This information helps businesses understand consumer preferences and tailor their products or marketing accordingly.
-
Quality Control: In a batch of 85 manufactured items, 25 were found to be defective. This represents a defect rate of approximately 29.41%, highlighting the need for quality control improvements in the manufacturing process.
Beyond the Basics: Exploring Proportions and Ratios
The concept of "25 out of 85" extends beyond simple percentage calculations. Understanding proportions and ratios allows us to solve more complex problems involving similar relationships. For instance, if we know that 25 out of 85 items are defective, we can use this ratio to predict the number of defective items in a larger batch. If we have a batch of 170 items, we can set up a proportion:
25/85 = x/170
Solving for x (the number of defective items in the 170-item batch), we find that x = 50. This means we can expect approximately 50 defective items in a batch of 170, based on the initial ratio.
Frequently Asked Questions (FAQs)
Q1: What is the difference between a fraction and a ratio?
A fraction represents a part of a whole, while a ratio compares two quantities. Though often expressed similarly, a ratio can compare parts of different wholes, while a fraction typically represents a part of a single whole.
Q2: Is there a more accurate way to represent 25 out of 85 than 29.41%?
The percentage 29.41% is an approximation. To be more precise, you could express it as a fraction (5/17) or use more decimal places in the percentage (e.g., 29.41176%). The level of precision needed depends on the context.
Q3: How can I calculate percentages quickly without a calculator?
For simple percentages, you can use mental math techniques. For example, 10% of a number is easily found by moving the decimal point one place to the left. Other percentages can be broken down into simpler parts (e.g., 25% is ¼).
Q4: Can I use this method for other fractions like "15 out of 60"?
Absolutely! The methods described above – converting to a percentage, simplifying the fraction, and using proportions – can be applied to any fraction.
Conclusion: Mastering Fractions and Ratios
Understanding how to interpret and manipulate fractions like "25 out of 85" is a crucial skill in various aspects of life. By converting the fraction to a percentage (approximately 29.41%), simplifying it to its lowest terms (5/17), and applying the concept to real-world problems, we demonstrate the practical value of these mathematical concepts. This ability to analyze ratios and proportions is vital for making informed decisions, interpreting data, and solving problems in diverse fields, from academics to business and beyond. Remember that understanding the underlying principles empowers you to confidently approach similar challenges and enhance your problem-solving capabilities.
Latest Posts
Latest Posts
-
Beatles Monopoly Board
Sep 21, 2025
-
Opposite Of Diligent
Sep 21, 2025
-
1 8 As Fraction
Sep 21, 2025
-
70 Of 75
Sep 21, 2025
-
Ohshc Season 2
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.