Simplify 6 21
interactiveleap
Sep 21, 2025 · 6 min read
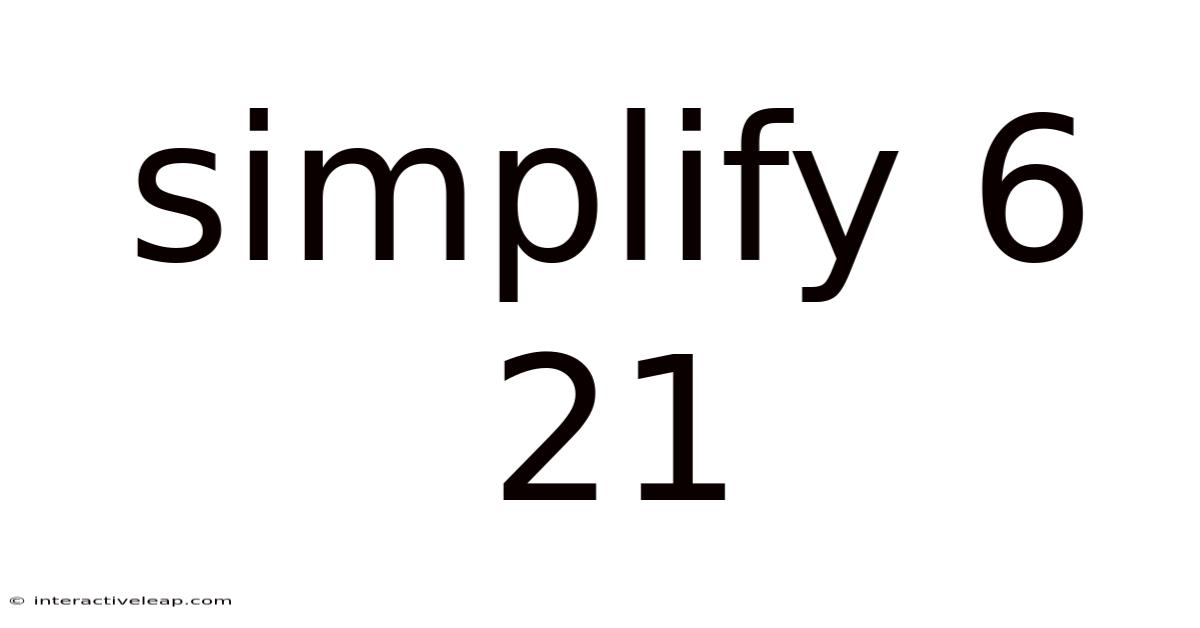
Table of Contents
Simplifying 6/21: A Comprehensive Guide to Fraction Reduction
Understanding how to simplify fractions is a fundamental skill in mathematics. This seemingly simple task lays the groundwork for more complex algebraic manipulations and problem-solving. This article will guide you through the process of simplifying the fraction 6/21, explaining the underlying principles and providing examples to solidify your understanding. We'll cover the core concept of finding the greatest common divisor (GCD), exploring different methods to determine it, and finally, applying this knowledge to simplify various fractions. By the end, you'll not only know how to simplify 6/21 but also possess a robust understanding of fraction reduction that you can apply to any fraction.
Introduction: What Does it Mean to Simplify a Fraction?
Simplifying a fraction, also known as reducing a fraction to its lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. In simpler terms, we're aiming to express the fraction in its simplest form, representing the same value but using the smallest possible whole numbers. The fraction 6/21, for example, can be simplified because both 6 and 21 share common factors. Our goal is to find the simplest form of this fraction.
Understanding Greatest Common Divisor (GCD)
The key to simplifying fractions lies in understanding the concept of the Greatest Common Divisor (GCD), also known as the Greatest Common Factor (GCF). The GCD of two or more numbers is the largest number that divides each of them without leaving a remainder. To simplify 6/21, we need to find the GCD of 6 and 21.
Methods for Finding the GCD
Several methods can be used to determine the GCD of two numbers:
-
Listing Factors: This method involves listing all the factors of each number and identifying the largest common factor.
- Factors of 6: 1, 2, 3, 6
- Factors of 21: 1, 3, 7, 21
The largest number that appears in both lists is 3. Therefore, the GCD of 6 and 21 is 3.
-
Prime Factorization: This method involves expressing each number as a product of its prime factors. The GCD is then the product of the common prime factors raised to the lowest power.
- Prime factorization of 6: 2 x 3
- Prime factorization of 21: 3 x 7
The only common prime factor is 3. Therefore, the GCD of 6 and 21 is 3.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide 21 by 6: 21 = 6 x 3 + 3
- Divide 6 by the remainder 3: 6 = 3 x 2 + 0
The last non-zero remainder is 3, so the GCD of 6 and 21 is 3.
Simplifying 6/21
Now that we've established that the GCD of 6 and 21 is 3, we can simplify the fraction 6/21:
-
Divide both the numerator and the denominator by the GCD:
6 ÷ 3 = 2 21 ÷ 3 = 7
-
The simplified fraction is: 2/7
Therefore, 6/21 simplified to its lowest terms is 2/7. This means that 6/21 and 2/7 represent the same value; they are equivalent fractions.
Visual Representation
Imagine you have a pizza cut into 21 slices. You have 6 of those slices (6/21). If you group those slices into sets of 3, you'll have 2 sets of 3 slices. The pizza is now considered to have 7 groups of 3 slices (21/3 = 7). You still possess 2 of these groups (2/7), representing the same amount of pizza.
More Examples of Fraction Simplification
Let's practice simplifying some more fractions using the methods discussed above:
-
Simplify 12/18:
- Factors of 12: 1, 2, 3, 4, 6, 12
- Factors of 18: 1, 2, 3, 6, 9, 18
GCD = 6 12 ÷ 6 = 2 18 ÷ 6 = 3 Simplified fraction: 2/3
-
Simplify 24/36:
- Prime factorization of 24: 2³ x 3
- Prime factorization of 36: 2² x 3²
GCD = 2² x 3 = 12 24 ÷ 12 = 2 36 ÷ 12 = 3 Simplified fraction: 2/3
-
Simplify 15/45:
Using the Euclidean Algorithm:
- 45 ÷ 15 = 3 + 0
GCD = 15 15 ÷ 15 = 1 45 ÷ 15 = 3 Simplified fraction: 1/3
Importance of Simplifying Fractions
Simplifying fractions is crucial for several reasons:
- Clarity: Simplified fractions are easier to understand and interpret. 2/7 is much clearer than 6/21.
- Calculations: Simplifying fractions before performing calculations (addition, subtraction, multiplication, division) simplifies the process and reduces the risk of errors.
- Comparison: Comparing simplified fractions is easier than comparing unsimplified fractions.
- Real-world applications: Simplifying fractions is essential in various real-world applications, including cooking, construction, engineering, and finance.
Frequently Asked Questions (FAQ)
-
Q: What if the GCD is 1?
- A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form and cannot be simplified further. This means the numerator and denominator share no common factors other than 1.
-
Q: Can I simplify a fraction by dividing the numerator and denominator by any common factor?
- A: Yes, you can divide the numerator and denominator by any common factor. However, for efficiency, it's best to divide by the greatest common divisor (GCD) to reach the simplest form in a single step. Dividing by a smaller common factor will require multiple steps.
-
Q: What happens if I divide the numerator and denominator by a number that is not a common factor?
- A: You will obtain an incorrect, non-equivalent fraction. The value of the fraction will change. Always ensure you divide both the numerator and the denominator by a common factor.
-
Q: Are there any online tools or calculators to help simplify fractions?
- A: While readily available online, the focus here is on understanding the underlying mathematical principles. Utilizing a calculator should only supplement your comprehension, not replace it. The process of manually simplifying fractions strengthens your mathematical foundation.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental mathematical skill with broad applications. By understanding the concept of the greatest common divisor and applying the methods outlined in this article—listing factors, prime factorization, and the Euclidean algorithm—you can confidently simplify any fraction. Remember, the goal is to find the equivalent fraction with the smallest possible whole numbers in the numerator and denominator, ensuring accuracy and clarity in your mathematical work. Regular practice will solidify your understanding and make this task effortless. From simplifying simple fractions like 6/21 to tackling more complex ones, the principles remain the same, empowering you with a valuable mathematical tool for various applications.
Latest Posts
Latest Posts
-
135kg In Pounds
Sep 21, 2025
-
Square Root 23
Sep 21, 2025
-
Villa La Rotonda
Sep 21, 2025
-
3 4 11
Sep 21, 2025
-
82 9kg In Stones
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Simplify 6 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.