3 4 11
interactiveleap
Sep 21, 2025 · 6 min read
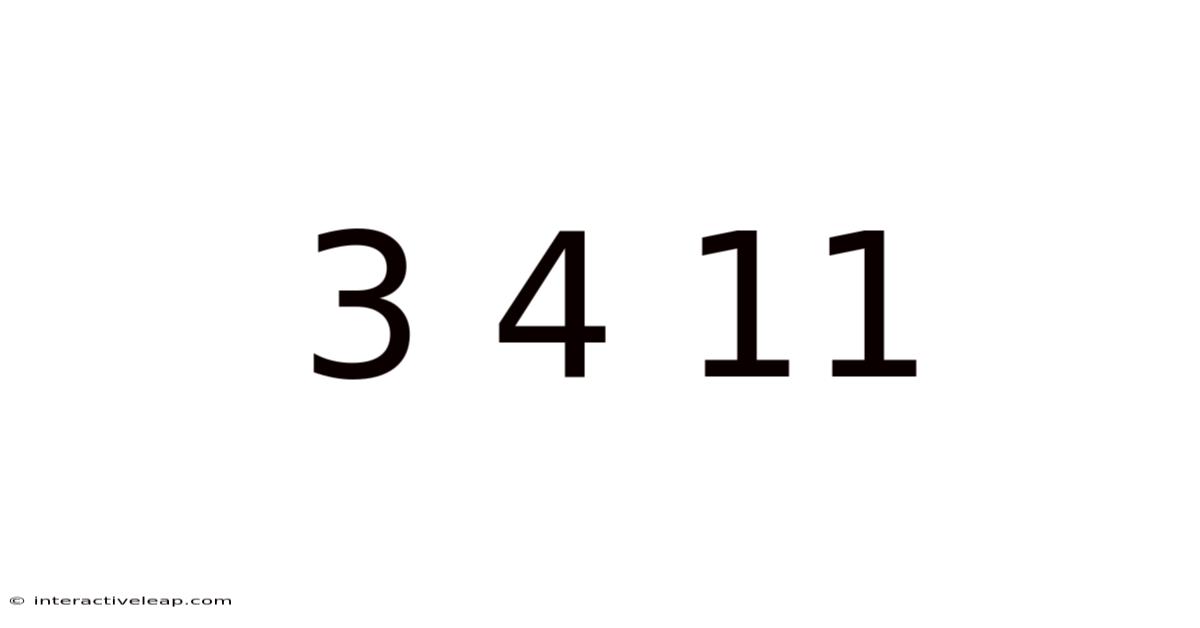
Table of Contents
Decoding the Mysterious Sequence: 3, 4, 11 – A Deep Dive into Number Patterns and Problem-Solving
The sequence 3, 4, 11… might seem innocuous at first glance. Just three numbers, seemingly random. But hidden within this simple sequence lies a world of mathematical possibilities and problem-solving strategies. This article will embark on a journey to explore various approaches to understanding this sequence, delving into different mathematical concepts and demonstrating how seemingly simple problems can lead to surprisingly complex solutions. We'll uncover potential patterns, examine underlying principles, and even explore the creative freedom in generating a sequence with only a partial given set. This investigation aims to not only find a solution but to understand the process of mathematical discovery.
Introduction: The Allure of Number Sequences
Number sequences have fascinated mathematicians and puzzle enthusiasts for centuries. They represent a fundamental aspect of mathematics, providing a gateway to explore concepts like patterns, logic, and algorithms. The beauty lies in the seemingly infinite possibilities that can be generated from a simple starting point. Sequences can be arithmetic (with a constant difference), geometric (with a constant ratio), or follow far more intricate rules involving combinations, primes, or even fractal geometry. Our investigation into the sequence 3, 4, 11 will highlight the diversity of approaches available when tackling such a problem.
Method 1: Searching for Arithmetic or Geometric Progression
The most straightforward approach is to look for a simple arithmetic or geometric progression. An arithmetic progression has a constant difference between consecutive terms. A geometric progression has a constant ratio between consecutive terms.
Let's check:
- Arithmetic: The difference between 4 and 3 is 1. The difference between 11 and 4 is 7. There's no constant difference here, ruling out a simple arithmetic progression.
- Geometric: The ratio between 4 and 3 is 4/3. The ratio between 11 and 4 is 11/4. Again, no constant ratio, eliminating a simple geometric progression.
Method 2: Exploring Polynomial Relationships
If the sequence isn't arithmetic or geometric, a more complex relationship might exist. We can explore the possibility of a polynomial relationship. A polynomial of degree n will have n+1 coefficients to determine. Since we only have three terms, we can at most fit a quadratic equation (a polynomial of degree 2).
Let's assume the sequence follows a quadratic equation of the form: an² + bn + c where 'a', 'b', and 'c' are constants.
We have three equations based on our sequence:
- For n = 1: a(1)² + b(1) + c = 3 => a + b + c = 3
- For n = 2: a(2)² + b(2) + c = 4 => 4a + 2b + c = 4
- For n = 3: a(3)² + b(3) + c = 11 => 9a + 3b + c = 11
Solving this system of three linear equations with three unknowns (a, b, c) yields a solution. Using substitution or matrix methods, we can find the values of a, b, and c. This would allow us to predict the next terms in the sequence. The solution to this system will provide a quadratic equation that fits the given sequence. This is a standard algebraic technique frequently used in data fitting and extrapolation.
Solving the system will give specific values for a, b, and c, allowing us to extrapolate the sequence using the resulting quadratic formula.
Method 3: Investigating Differences and Second Differences
Another common technique for analyzing sequences is to look at the differences between consecutive terms. This is particularly useful for polynomial sequences. Let’s calculate the first differences:
- 4 - 3 = 1
- 11 - 4 = 7
The first differences are not constant. Let’s calculate the second differences:
- 7 - 1 = 6
The second differences are constant. A constant second difference suggests a quadratic relationship, aligning with our findings in Method 2.
Method 4: Exploring Recursive Relationships
A recursive relationship defines each term in the sequence based on the preceding terms. There could be multiple recursive relationships that would fit the first three terms. For example, one possible recursive relationship could be:
- a<sub>n+2</sub> = a<sub>n+1</sub> + 2a<sub>n</sub> + 2
Let’s test this:
- a<sub>1</sub> = 3
- a<sub>2</sub> = 4
- a<sub>3</sub> = 4 + 2(3) + 2 = 12 (This doesn’t match our sequence)
This highlights the fact that multiple recursive relationships can potentially fit a small initial segment of a sequence. Finding a robust and meaningful relationship often requires more terms.
Method 5: The Role of Creativity and Multiple Solutions
It’s crucial to recognize that, with only three terms, there's no single definitive solution. Many different mathematical rules could generate a sequence beginning with 3, 4, 11. The lack of a clear pattern emphasizes the creativity involved in mathematics. The process of exploration is just as important as finding a solution. Different approaches may lead to different interpretations and extrapolations of the sequence.
For instance, one might discover a sequence based on prime numbers or other mathematical properties hidden within a more complex formula, only discernible when more terms of the sequence are given.
Method 6: The Importance of Context
In real-world applications, the context surrounding a number sequence often provides crucial clues. If the sequence arose from a specific problem or phenomenon (e.g., a physics experiment, a biological observation, or a coding challenge), this context could significantly narrow the possibilities and point towards a more meaningful relationship. Without context, we are left with a vast field of potential interpretations.
Explanation of the Mathematical Principles Involved
This investigation touches upon several key mathematical principles:
- Sequences and Series: The core concept underpinning the analysis.
- Arithmetic and Geometric Progressions: Fundamental types of sequences with easily identifiable patterns.
- Polynomial Interpolation: The technique used to fit a polynomial equation to a set of data points. This is a powerful tool in numerous fields, from data analysis to computer graphics.
- Recursive Relationships: Defining a sequence by relating each term to its predecessors. These are often found in computer science and algorithms.
- Difference Equations: Analyzing the differences between consecutive terms to identify patterns.
- Systems of Linear Equations: Solving multiple equations simultaneously to find the coefficients of a polynomial.
Frequently Asked Questions (FAQ)
-
Q: Is there only one correct answer? A: No, with limited data, several patterns could potentially generate the sequence 3, 4, 11.
-
Q: How can I find the next number in the sequence? A: That depends on the pattern you choose to follow. Based on the quadratic solution derived from Method 2, you would substitute the next value of 'n' into the equation.
-
Q: What if I had more numbers in the sequence? A: More data would constrain the possible solutions and improve the accuracy of any fitted model, making it easier to identify a meaningful pattern.
-
Q: What are some other methods to analyze number sequences? A: Other methods include exploring modular arithmetic, looking for relationships with prime numbers, examining factorials or combinations, or even investigating links with geometrical patterns.
Conclusion: The Ongoing Journey of Mathematical Discovery
The seemingly simple sequence 3, 4, 11 presents a fascinating challenge that highlights the richness and complexity of mathematical problem-solving. While we explored several approaches to find potential patterns, the crucial takeaway is the process itself. The lack of a single definitive answer underscores the importance of critical thinking, creativity, and the exploration of multiple perspectives. The journey of mathematical investigation is often more valuable than reaching a single destination, especially when grappling with incomplete information. Further exploration, with more terms added to the sequence, might reveal a hidden elegance or a surprisingly intricate structure. This simple sequence serves as a powerful reminder that even the simplest mathematical problems can harbor a wealth of complexity and possibility.
Latest Posts
Latest Posts
-
Quadratic Sequence Examples
Sep 21, 2025
-
86 5kg In Stones
Sep 21, 2025
-
900 X 4
Sep 21, 2025
-
2 000 Ft
Sep 21, 2025
-
64 Divided 2
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 4 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.