64 Divided 2
interactiveleap
Sep 21, 2025 · 6 min read
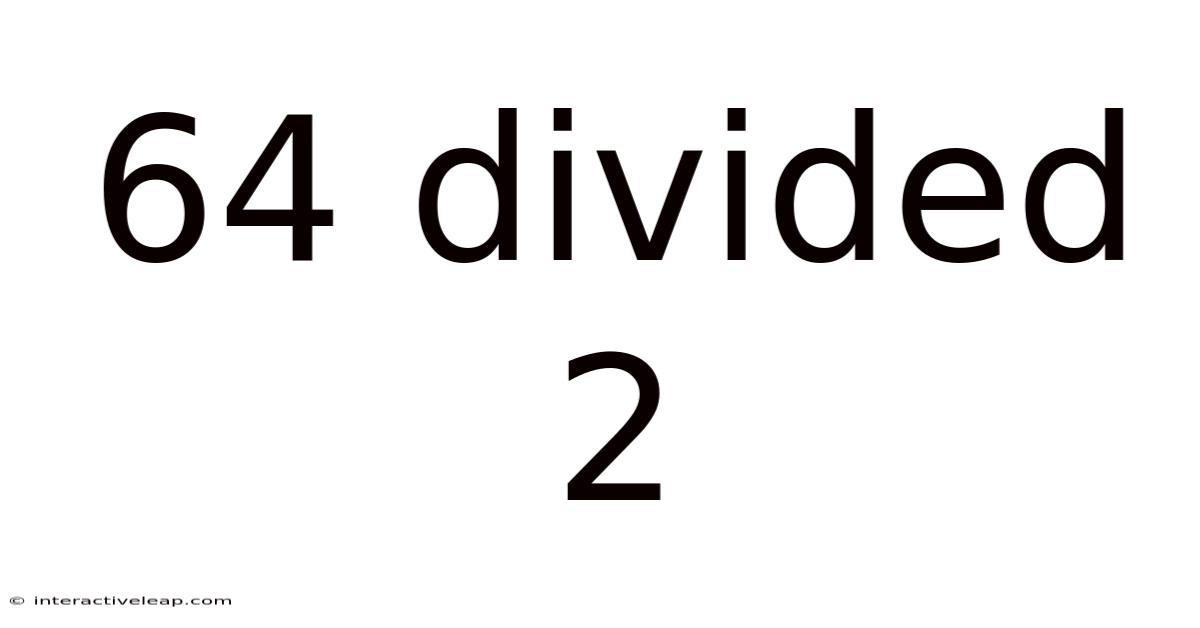
Table of Contents
64 Divided by 2: A Deep Dive into Simple Division and its Applications
This article explores the seemingly simple calculation of 64 divided by 2, delving beyond the immediate answer to uncover the underlying mathematical principles, explore various methods of solving the problem, and demonstrate its relevance in diverse real-world applications. Understanding this basic operation forms a crucial foundation for more complex mathematical concepts and problem-solving skills. Whether you're a student refreshing your arithmetic skills or an adult seeking to understand the fundamentals of mathematics, this comprehensive guide will provide a thorough and engaging explanation.
Introduction: The Fundamentals of Division
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts. In the expression "64 divided by 2," we are essentially asking: "How many times does 2 fit into 64?" The answer, as we'll explore in detail, is 32. This simple equation forms the basis for understanding more complex division problems involving larger numbers, fractions, decimals, and even algebraic expressions.
Method 1: Long Division
Long division is a traditional method used to solve division problems, particularly those involving larger numbers. While a calculator provides an instant answer, understanding the process of long division is crucial for developing a strong mathematical foundation. Let's break down 64 divided by 2 using this method:
-
Set up the problem: Write 64 inside the long division symbol (⟌) and 2 outside.
-
Divide the tens: How many times does 2 go into 6? It goes in 3 times (3 x 2 = 6). Write the 3 above the 6 in the quotient.
-
Multiply and subtract: Multiply the quotient digit (3) by the divisor (2): 3 x 2 = 6. Subtract this result from the tens digit of the dividend (6 - 6 = 0).
-
Bring down the ones: Bring down the next digit (4) from the dividend.
-
Divide the ones: How many times does 2 go into 4? It goes in 2 times (2 x 2 = 4). Write the 2 above the 4 in the quotient.
-
Multiply and subtract: Multiply the quotient digit (2) by the divisor (2): 2 x 2 = 4. Subtract this result from the ones digit of the dividend (4 - 4 = 0).
-
The result: There is no remainder. The quotient (the answer) is 32.
Therefore, 64 ÷ 2 = 32
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the divisor (2) from the dividend (64) until you reach zero. The number of times you subtract represents the quotient. While less efficient for larger numbers, it provides a visual understanding of division.
64 - 2 = 62 62 - 2 = 60 60 - 2 = 58 ...and so on until you reach 0. Counting the number of subtractions will yield the answer, 32. This method is excellent for demonstrating the concept of division, particularly for younger learners.
Method 3: Halving
Since we are dividing by 2, we can use the simple method of halving. Halving means dividing a number by 2. To solve 64 divided by 2, simply halve 64:
64 / 2 = 32
Method 4: Using Multiplication
Division and multiplication are inverse operations. This means that if we know the multiplication fact related to the division problem, we can easily find the answer. Since 2 x 32 = 64, then 64 ÷ 2 = 32. This approach is useful for smaller numbers where multiplication facts are easily recalled.
The Significance of 64 and 2: Binary and Computer Science
The numbers 64 and 2 hold particular significance in computer science and the binary number system. Binary uses only two digits, 0 and 1, to represent all numbers. 64 is a power of 2 (2<sup>6</sup> = 64). This makes it a crucial number in data storage and processing. For instance, 64 bits are commonly used to represent data in computer systems, influencing the capacity and performance of computer hardware and software. The division of 64 by 2 reflects a fundamental operation in binary arithmetic, involving shifting bits within a binary number.
Real-World Applications of Division: Examples
The seemingly simple calculation of 64 divided by 2 has wide-ranging applications in everyday life and various fields:
-
Sharing Equally: Imagine you have 64 candies and want to share them equally among 2 friends. Dividing 64 by 2 tells you each friend will receive 32 candies.
-
Calculating Unit Prices: If a pack of 64 pencils costs $2, dividing the cost by the number of pencils ($2/64) gives the unit price of each pencil.
-
Measuring: If a 64-meter-long rope needs to be cut into two equal pieces, dividing 64 by 2 determines that each piece will be 32 meters long.
-
Data Processing: In computer science, dividing large datasets into smaller, more manageable chunks often involves calculations similar to 64 divided by 2, though likely with much larger numbers.
-
Cooking and Baking: Many recipes require halving or doubling ingredients. Dividing ingredient quantities by 2 is a common task.
-
Engineering and Physics: Many formulas in engineering and physics involve division. Understanding the fundamental principles of division is essential for solving various problems in these fields.
-
Financial Calculations: Dividing total income by the number of months provides the average monthly income.
Frequently Asked Questions (FAQs)
-
What is the remainder when 64 is divided by 2? There is no remainder because 2 divides 64 evenly.
-
How can I check my answer? Multiply the quotient (32) by the divisor (2). If the result is the dividend (64), your answer is correct.
-
What if I'm dividing a larger number by 2? The same principles apply; you can use long division, repeated subtraction, or halving. For larger numbers, calculators are often more efficient.
-
Is there a shortcut for dividing by 2? Yes, halving the number is a quick method. Simply divide the number in half.
-
Why is it important to learn division? Division is a foundational mathematical operation crucial for various calculations and problem-solving in everyday life, professional contexts, and advanced studies.
Conclusion: Beyond the Basics
While 64 divided by 2 provides a straightforward answer (32), exploring this simple equation reveals a wealth of underlying mathematical concepts and practical applications. Mastering the principles of division, through various methods like long division, repeated subtraction, or halving, establishes a strong foundation for tackling more complex mathematical challenges. The seemingly simple act of dividing 64 by 2 is a gateway to understanding more intricate concepts, highlighting the importance of developing solid foundational knowledge in arithmetic. This understanding extends beyond the classroom and finds practical application in various aspects of life. Whether you are a student learning arithmetic for the first time or an adult seeking to refresh fundamental mathematical concepts, understanding the mechanics and significance of division will prove beneficial in numerous contexts.
Latest Posts
Latest Posts
-
35 Of 220
Sep 21, 2025
-
Sole Trader Disadvantages
Sep 21, 2025
-
7 7km In Miles
Sep 21, 2025
-
Burrow With Burrow
Sep 21, 2025
-
15 Of 21
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 64 Divided 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.