Simplify 12 20
interactiveleap
Sep 24, 2025 · 5 min read
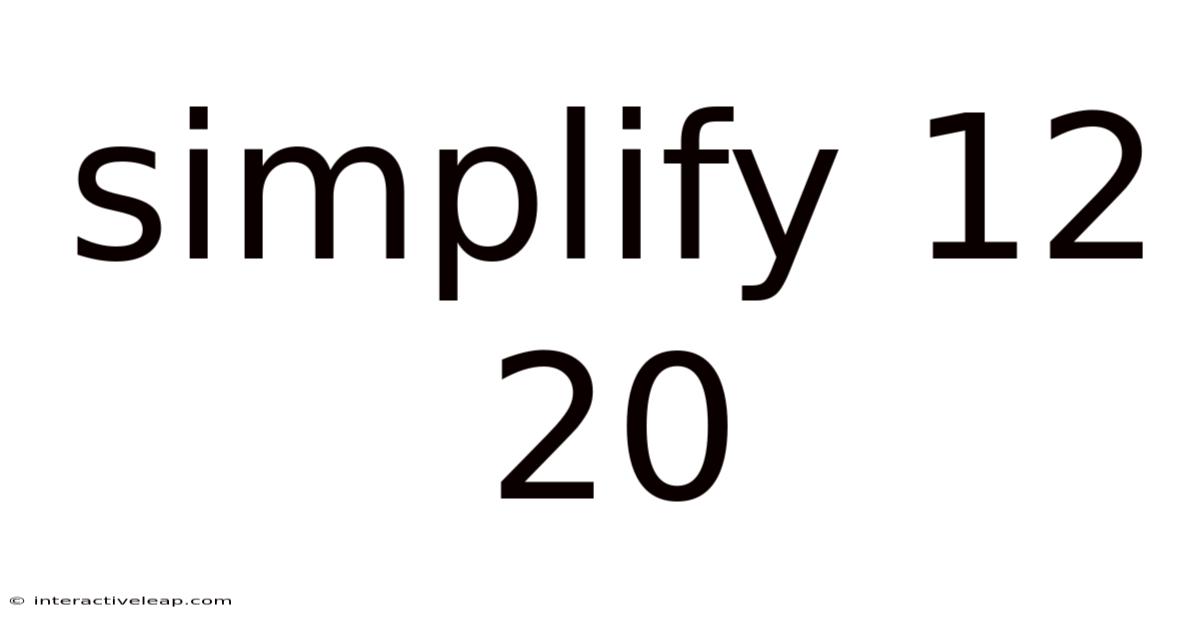
Table of Contents
Simplifying 12/20: A Comprehensive Guide to Fraction Reduction
Understanding fractions is a fundamental concept in mathematics, crucial for various applications in everyday life and advanced studies. This article delves into the simplification of the fraction 12/20, explaining the process step-by-step, providing the scientific rationale behind it, and addressing frequently asked questions. We'll explore different methods for simplifying fractions, ensuring you not only understand how to reduce 12/20 but also gain a broader understanding of fraction simplification techniques. By the end, you'll be confident in simplifying various fractions and appreciate the elegance of mathematical simplification.
Introduction: What Does Simplifying Fractions Mean?
Simplifying a fraction, also known as reducing a fraction to its simplest form, means finding an equivalent fraction where the numerator (the top number) and the denominator (the bottom number) have no common factors other than 1. In essence, we're finding the most concise representation of the fraction's value. For example, the fraction 12/20 represents a portion of a whole, and simplifying it helps us understand this portion more clearly.
Simplifying fractions is essential for several reasons:
- Clarity: Simplified fractions are easier to understand and visualize.
- Comparison: Comparing simplified fractions is simpler than comparing complex ones.
- Calculations: Simplified fractions make subsequent calculations more manageable and less prone to error.
Step-by-Step Simplification of 12/20
To simplify 12/20, we need to find the greatest common divisor (GCD) of 12 and 20. The GCD is the largest number that divides both 12 and 20 without leaving a remainder.
Method 1: Finding the GCD using prime factorization
-
Prime Factorization of 12: We break down 12 into its prime factors: 12 = 2 x 2 x 3 (or 2² x 3)
-
Prime Factorization of 20: We break down 20 into its prime factors: 20 = 2 x 2 x 5 (or 2² x 5)
-
Identifying Common Factors: Both 12 and 20 share two factors of 2 (2²).
-
Calculating the GCD: The GCD of 12 and 20 is 2 x 2 = 4.
-
Simplifying the Fraction: We divide both the numerator and the denominator by the GCD (4): 12 ÷ 4 = 3 and 20 ÷ 4 = 5.
Therefore, the simplified fraction is 3/5.
Method 2: Using the Euclidean Algorithm
The Euclidean algorithm is another efficient method for finding the GCD, particularly useful for larger numbers.
-
Divide the larger number by the smaller number: 20 ÷ 12 = 1 with a remainder of 8.
-
Replace the larger number with the smaller number and the smaller number with the remainder: Now we consider 12 and 8.
-
Repeat the process: 12 ÷ 8 = 1 with a remainder of 4.
-
Repeat again: 8 ÷ 4 = 2 with a remainder of 0.
-
The GCD is the last non-zero remainder: The GCD is 4.
-
Simplify the fraction: Divide both numerator and denominator by 4, resulting in 3/5.
Method 3: Listing Factors (Suitable for smaller numbers)
This method involves listing the factors of both the numerator and denominator and identifying the greatest common factor.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 20: 1, 2, 4, 5, 10, 20
The greatest common factor is 4. Dividing both numerator and denominator by 4 gives us 3/5.
The Mathematical Rationale Behind Fraction Simplification
Simplifying fractions relies on the fundamental principle of equivalent fractions. Multiplying or dividing both the numerator and the denominator of a fraction by the same non-zero number does not change the value of the fraction. This is because we're essentially multiplying or dividing by 1 (e.g., 4/4 = 1).
When we simplify 12/20 to 3/5, we're dividing both the numerator and the denominator by their GCD (4). This division ensures that we're left with a fraction where the numerator and denominator share no common factors other than 1, representing the simplest form of the original fraction.
Visualizing Fraction Simplification
Imagine a pizza cut into 20 slices. The fraction 12/20 represents 12 out of 20 slices. If we group the slices into sets of 4, we have 3 groups of 4 slices out of 5 groups of 4 slices. This visually demonstrates the equivalence of 12/20 and 3/5. Both represent the same portion of the pizza.
Frequently Asked Questions (FAQ)
Q1: Is 3/5 the only simplified form of 12/20?
A1: Yes, 3/5 is the simplest form of 12/20 because 3 and 5 share no common factors other than 1.
Q2: What if I divide by a common factor but not the GCD?
A2: You'll obtain a simplified fraction, but it won't be in its simplest form. For example, dividing 12/20 by 2 gives 6/10, which is still reducible. Using the GCD ensures you reach the simplest form in one step.
Q3: Can I simplify fractions with negative numbers?
A3: Yes, the process remains the same. Determine the GCD of the absolute values of the numerator and denominator, and then apply the simplification. Remember to retain the negative sign if either the numerator or denominator (but not both) was initially negative. For example, -12/20 simplifies to -3/5.
Q4: How do I simplify more complex fractions?
A4: The process remains the same. Find the GCD of the numerator and denominator using prime factorization, the Euclidean algorithm, or listing factors and divide both by the GCD.
Q5: Why is simplifying fractions important in algebra?
A5: Simplifying fractions is crucial in algebra for simplifying expressions, solving equations, and working with rational expressions. Unsimplified fractions can make algebraic manipulations more complex and error-prone.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill with broad applications in mathematics and beyond. By understanding the methods of finding the greatest common divisor and applying the principles of equivalent fractions, you can confidently reduce any fraction to its simplest form. This article has explored various methods, explained the mathematical rationale, and answered common questions to solidify your understanding. Remember to practice regularly to build proficiency and develop a strong mathematical foundation. Mastering fraction simplification is a significant step towards a deeper understanding of mathematical concepts and problem-solving. The seemingly simple act of reducing 12/20 to 3/5 encapsulates the elegance and power of mathematical simplification.
Latest Posts
Latest Posts
-
20 Of 13000
Sep 24, 2025
-
1 25m In Feet
Sep 24, 2025
-
Drowned River Valley
Sep 24, 2025
-
80g In Ounces
Sep 24, 2025
-
1 6 Of 120
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Simplify 12 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.