1/6 Of 120
interactiveleap
Sep 24, 2025 · 6 min read
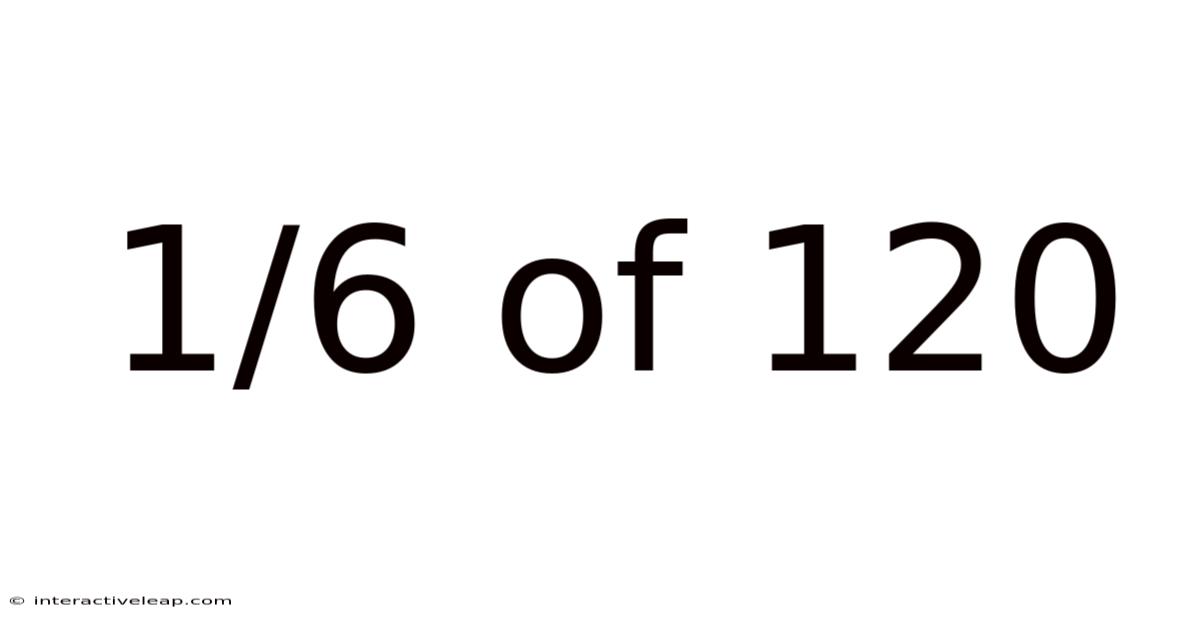
Table of Contents
Decoding 1/6 of 120: A Comprehensive Guide to Fractions and Division
Finding 1/6 of 120 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation opens the door to a deeper appreciation of fractions, division, and their real-world applications. This comprehensive guide will not only solve the problem but also explore the underlying mathematical concepts, provide various solution methods, and delve into the practical significance of fractional calculations. We'll explore different approaches, ensuring a firm grasp of the fundamentals for learners of all levels.
Introduction: Understanding Fractions and Division
Before diving into the specifics of calculating 1/6 of 120, let's refresh our understanding of key concepts. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered. In our case, 1/6 means one out of six equal parts.
Division, on the other hand, is the process of splitting a number into equal parts. Finding 1/6 of 120 is essentially dividing 120 into six equal parts and then taking one of those parts. Both fractions and division are fundamentally intertwined; they are different ways of representing the same underlying mathematical operation.
Method 1: Direct Multiplication
The most straightforward method to calculate 1/6 of 120 is through direct multiplication. We can express "of" as multiplication. Therefore, 1/6 of 120 can be written as:
(1/6) * 120
To perform this multiplication, we multiply the numerator (1) by 120 and then divide the result by the denominator (6):
(1 * 120) / 6 = 120 / 6 = 20
Therefore, 1/6 of 120 is 20.
Method 2: Division First, then Multiplication
Alternatively, we can first divide 120 by the denominator (6) and then multiply the result by the numerator (1). This approach provides a clearer visualization of the process:
120 / 6 = 20
20 * 1 = 20
Again, we arrive at the same answer: 1/6 of 120 is 20. This method highlights that finding a fraction of a number involves dividing the number by the denominator and then multiplying by the numerator.
Method 3: Simplifying the Fraction
Before performing the calculation, we can simplify the fraction if possible. While 1/6 is already in its simplest form, this method becomes more beneficial when dealing with more complex fractions. For instance, if we were to find 2/6 of 120, we could simplify 2/6 to 1/3 before proceeding with the calculation.
This simplification would look like this:
(2/6) * 120 = (1/3) * 120 = 120 / 3 = 40
This emphasizes the importance of simplifying fractions to make calculations easier and reduce errors.
Method 4: Visual Representation
For a more intuitive understanding, let's visualize the problem. Imagine we have 120 objects, such as apples. To find 1/6 of 120, we divide the 120 apples into six equal groups. Each group will contain:
120 / 6 = 20 apples
Therefore, 1/6 of the apples (one group) is 20 apples. This visual representation provides a concrete understanding of the fraction and the division process.
Real-World Applications
The calculation of fractions like 1/6 of 120 is not just an abstract mathematical exercise; it has numerous real-world applications. Here are a few examples:
-
Sharing Resources: Imagine you have 120 candies to share equally among six friends. Each friend would receive 1/6 of the total candies, which is 20 candies.
-
Calculating Discounts: A store offers a 1/6 discount on an item priced at $120. The discount amount would be 1/6 of $120, which is $20.
-
Portion Control: A recipe calls for 1/6 of a 120-gram ingredient. You would need 20 grams of that ingredient.
-
Data Analysis: In data analysis, you might need to find a fraction of a total dataset, such as determining 1/6 of 120 survey responses to analyze a specific segment.
These examples demonstrate the practical relevance of understanding fractions and their applications in everyday scenarios.
Extending the Concept: Working with More Complex Fractions
The principles discussed above can be applied to more complex fractions. For instance, to find 5/6 of 120, we would follow the same steps:
(5/6) * 120 = (5 * 120) / 6 = 600 / 6 = 100
Or, we could simplify the process by first dividing 120 by 6 and then multiplying by 5:
120 / 6 = 20
20 * 5 = 100
This showcases the versatility of these methods in handling various fractional calculations.
Decimals and Percentages: Alternative Representations
Fractions can also be expressed as decimals or percentages. 1/6 can be expressed as a decimal by dividing 1 by 6:
1 / 6 ≈ 0.1667
And as a percentage by multiplying the decimal by 100:
0.1667 * 100 ≈ 16.67%
Therefore, 1/6 of 120 can be calculated using these decimal or percentage representations as well:
0.1667 * 120 ≈ 20
16.67% of 120 ≈ 20
Frequently Asked Questions (FAQ)
Q1: What if the numerator is larger than the denominator?
A1: If the numerator is larger than the denominator, the fraction is called an improper fraction. This represents a value greater than 1. The calculation would still follow the same principles, but the result will be a number greater than the original value. For example, finding 7/6 of 120 would result in a value greater than 120.
Q2: How do I calculate fractions of numbers with decimals?
A2: The process remains the same. For example, to find 1/6 of 120.5, you would perform (1/6) * 120.5 = 20.0833.
Q3: Are there any online calculators or tools to help with fraction calculations?
A3: Yes, numerous online calculators are available that can assist with various fraction-related calculations, including finding fractions of numbers. These tools can be particularly helpful for complex calculations or for verifying your own work.
Q4: How can I improve my understanding of fractions?
A4: Consistent practice is key. Start with simple fractions and gradually move towards more complex ones. Visual aids, such as diagrams and real-world examples, can significantly aid understanding.
Conclusion: Mastering the Fundamentals
Calculating 1/6 of 120, while seemingly simple, provides a foundation for understanding fundamental mathematical concepts. Through different calculation methods, visual representations, and real-world applications, we've explored the multifaceted nature of this seemingly simple problem. Mastering these basic fractional calculations is crucial not only for academic success but also for navigating numerous practical situations in everyday life. Remember that consistent practice and a clear understanding of the underlying principles are key to building confidence and proficiency in working with fractions. The ability to effortlessly calculate fractions will undoubtedly empower you to tackle more complex mathematical challenges in the future.
Latest Posts
Latest Posts
-
X 4 3
Sep 24, 2025
-
350ml Bottle Water
Sep 24, 2025
-
Male Crown Tattoos
Sep 24, 2025
-
17c In F
Sep 24, 2025
-
10 12 Simplified
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1/6 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.