X 4 3
interactiveleap
Sep 24, 2025 · 6 min read
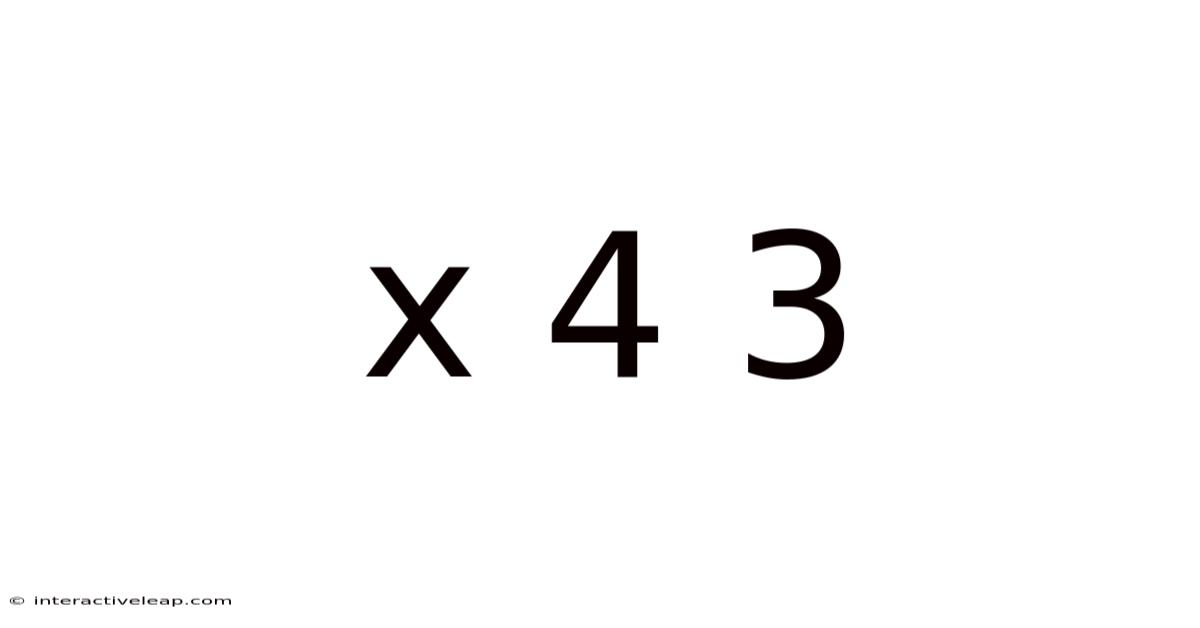
Table of Contents
Decoding x⁴ + 3: A Deep Dive into Polynomial Expressions and Their Applications
This article explores the seemingly simple expression x⁴ + 3, unraveling its mathematical properties, potential applications, and the broader context within which it exists. While seemingly basic, understanding this polynomial opens doors to comprehending more complex mathematical concepts and their real-world applications. We'll cover its factorization, graphing, the concept of roots (or zeros), and delve into related fields like calculus and numerical analysis. This exploration will be accessible to a wide audience, from high school students to those with a stronger mathematical background, offering a comprehensive and insightful look into the world of polynomial expressions.
Introduction to Polynomials: Understanding the Basics
Before diving into the specifics of x⁴ + 3, let's establish a fundamental understanding of polynomials. A polynomial is an expression consisting of variables (like x), coefficients (numbers multiplying the variables), and exponents (positive whole numbers indicating the power of the variable). Our expression, x⁴ + 3, is a polynomial. More specifically, it is a quartic polynomial because the highest power of the variable (x) is 4. The term x⁴ has a coefficient of 1 (implied), and the constant term is 3.
Polynomials are fundamental building blocks in algebra and calculus. They are used to model numerous real-world phenomena, from the trajectory of a projectile to the growth of a population. Their properties – including roots, derivatives, and integrals – are extensively studied in mathematics.
Factoring x⁴ + 3: A Journey into Algebraic Manipulation
Factoring a polynomial involves expressing it as a product of simpler polynomials. Factoring x⁴ + 3 is not straightforward. While we can factor many polynomials easily using techniques like difference of squares or grouping, x⁴ + 3 presents a unique challenge. It doesn't readily factor using standard algebraic methods over the real numbers.
To understand why, consider the concept of roots. The roots of a polynomial are the values of x that make the polynomial equal to zero. Finding the roots is often closely tied to factoring. If we could find the roots of x⁴ + 3 = 0, we could potentially factor the polynomial. However, solving x⁴ = -3 reveals that the roots are complex numbers.
Complex Numbers: Complex numbers involve the imaginary unit i, where i² = -1. The solutions to x⁴ = -3 are complex, involving both real and imaginary parts. These solutions can be expressed using polar form or Cartesian form (a + bi). Using the polar form, we can express the roots in terms of angles and magnitudes.
While we can’t easily factor x⁴ + 3 over real numbers, the use of complex numbers allows for factorization into quadratic factors. This factorization would involve complex coefficients.
Graphing x⁴ + 3: A Visual Representation
Visualizing the polynomial is another valuable approach to understanding its behavior. Graphing x⁴ + 3 reveals key characteristics.
- Shape: The graph of x⁴ + 3 is a parabola-like curve, but flatter near the origin and steeper as x moves away from zero. This is typical for even-powered polynomials.
- Y-intercept: The y-intercept is found by setting x = 0, giving us a y-value of 3. The graph intersects the y-axis at (0, 3).
- Symmetry: The graph is symmetric about the y-axis. This is a characteristic of even-powered polynomials where only even powers of x are present.
- No x-intercepts: Importantly, the graph has no x-intercepts (points where the graph crosses the x-axis). This is because the roots of the polynomial are complex, meaning there are no real values of x that make x⁴ + 3 equal to zero.
Finding the Roots: Exploring Complex Numbers and the Fundamental Theorem of Algebra
The Fundamental Theorem of Algebra states that a polynomial of degree n has exactly n roots, counting multiplicities, in the complex number system. Since x⁴ + 3 is a quartic polynomial (degree 4), it has four roots. These roots are complex, as we've already discussed.
Finding the roots involves solving the equation x⁴ = -3. This can be done using several methods, including:
- De Moivre's Theorem: This theorem allows us to find the roots of complex numbers in polar form.
- Numerical Methods: If analytical methods are too complex, numerical methods such as the Newton-Raphson method can provide approximate solutions.
Applications: Connecting Theory to Practice
While x⁴ + 3 might seem abstract, polynomials similar to this form appear in various applications:
- Physics: Equations describing oscillations or wave phenomena often involve polynomials of higher degree. Modeling complex oscillations or resonant frequencies might involve similar polynomial expressions.
- Engineering: Polynomial approximations are used in many engineering fields, including signal processing and control systems. Approximating complex functions with polynomials simplifies calculations.
- Computer Science: Polynomial interpolation and approximation are essential in computer graphics, numerical analysis, and algorithm design. Efficient algorithms for finding roots are vital.
- Economics: Polynomial functions can model various economic relationships, although simpler models are often preferred for their ease of interpretation.
Calculus and x⁴ + 3: Derivatives and Integrals
Calculus provides further insights into the behavior of x⁴ + 3.
- Derivative: The derivative of x⁴ + 3 is 4x³. The derivative represents the instantaneous rate of change of the function. The derivative being zero indicates critical points (local minima or maxima). In this case, the derivative is zero only at x = 0, indicating a local minimum at (0,3).
- Integral: The indefinite integral of x⁴ + 3 is (1/5)x⁵ + 3x + C, where C is the constant of integration. The integral represents the area under the curve of the function.
Advanced Topics and Further Exploration
For those interested in delving deeper, here are some advanced topics related to x⁴ + 3 and polynomials in general:
- Galois Theory: This area of abstract algebra explores the solvability of polynomial equations by radicals. It reveals that some polynomials, particularly those of degree 5 or higher, cannot be solved using only radicals.
- Numerical Analysis: Efficient algorithms for finding roots and approximating polynomials are crucial in numerical analysis. Methods like Newton-Raphson and bisection are commonly used.
- Abstract Algebra: Polynomials play a central role in abstract algebra, particularly in the study of rings and fields.
Frequently Asked Questions (FAQ)
Q: Can x⁴ + 3 be factored using only real numbers?
A: No, x⁴ + 3 cannot be factored into simpler polynomials using only real coefficients. Its roots are complex numbers.
Q: What are the practical uses of understanding complex roots?
A: Complex roots, while seemingly abstract, are essential in many fields. They appear in the analysis of oscillations, wave phenomena, and in the design of stable control systems.
Q: How do I solve x⁴ = -3?
A: Solving x⁴ = -3 requires using complex numbers. One approach is to use De Moivre's Theorem, which provides a systematic way to find the roots of complex numbers.
Q: What is the significance of the Fundamental Theorem of Algebra?
A: The Fundamental Theorem of Algebra guarantees the existence of roots for any polynomial, even if those roots are complex. It underpins much of polynomial analysis.
Conclusion: The Enduring Significance of a Simple Polynomial
While initially appearing simple, the expression x⁴ + 3 provides a rich avenue for exploring fundamental concepts in algebra, calculus, and numerical analysis. Its factorization into complex factors, its graphical representation, and its implications in various scientific and engineering fields highlight the deep connections within mathematics and its vast applications in the real world. This exploration hopefully demonstrates that even seemingly straightforward mathematical expressions can hold unexpected depth and significance, enriching our understanding of the world around us.
Latest Posts
Latest Posts
-
1 6kg In Lbs
Sep 24, 2025
-
240kg In Stone
Sep 24, 2025
-
Psi In Kpa
Sep 24, 2025
-
Cos Of 35
Sep 24, 2025
-
1 6 Oz Ml
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about X 4 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.