Factorise 5x 15
interactiveleap
Sep 21, 2025 · 6 min read
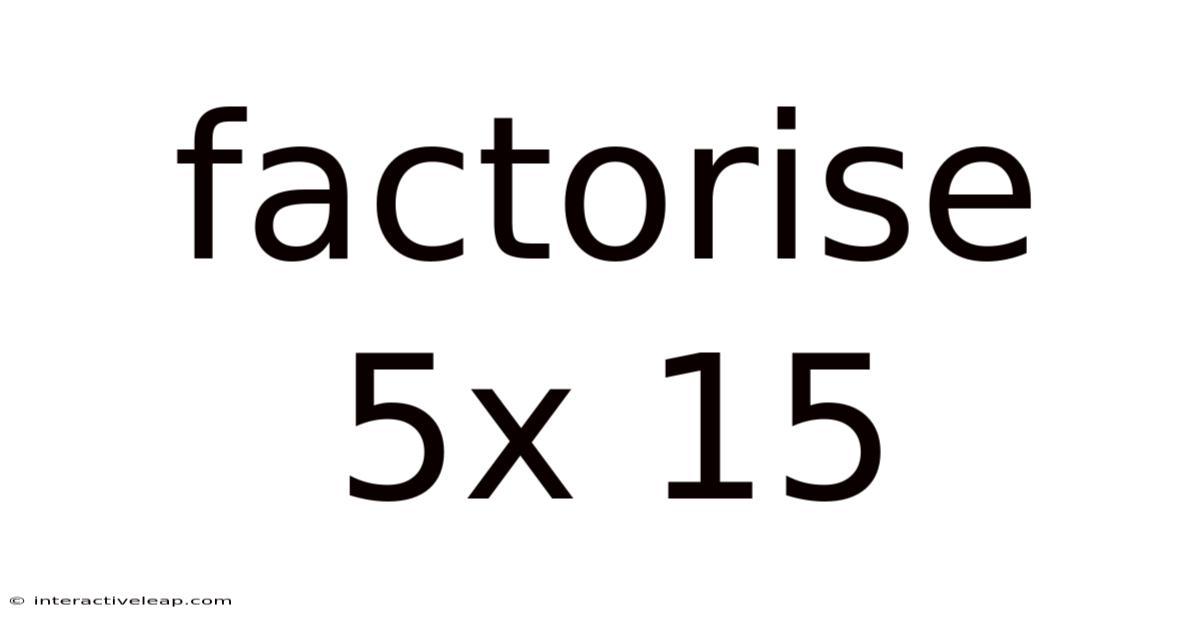
Table of Contents
Factorising 5x + 15: A Comprehensive Guide
This article provides a comprehensive guide on factorising the algebraic expression 5x + 15. We'll explore the fundamental concepts of factorisation, delve into the step-by-step process of solving this specific problem, and examine the underlying mathematical principles. We will also address common misconceptions and answer frequently asked questions, ensuring a thorough understanding for learners of all levels. Understanding factorisation is crucial for simplifying algebraic expressions and solving various mathematical problems.
Introduction to Factorisation
Factorisation, in algebra, is the process of breaking down an expression into smaller, simpler expressions that, when multiplied together, give the original expression. Think of it like reverse multiplication. For example, the number 12 can be factorised as 2 x 6, 3 x 4, or 2 x 2 x 3. Similarly, algebraic expressions can be factorised into their constituent parts. This skill is essential for simplifying expressions, solving equations, and working with polynomials. The ability to efficiently factorise algebraic expressions is a cornerstone of advanced algebra and calculus.
Step-by-Step Factorisation of 5x + 15
The expression 5x + 15 appears simple, but understanding its factorisation reveals fundamental algebraic concepts. Here’s how we factorise it:
1. Identify the Common Factor:
The first step in factorising any algebraic expression is to identify the greatest common factor (GCF) of all the terms. In the expression 5x + 15, we have two terms: 5x and 15.
- The factors of 5x are 5 and x.
- The factors of 15 are 3, 5, and 15.
The greatest common factor of 5x and 15 is 5.
2. Factor Out the GCF:
Once the GCF is identified, we factor it out from each term in the expression. This means we divide each term by the GCF and write the result within parentheses, with the GCF outside the parentheses.
(5x + 15) = 5(x + 3)
This is because: 5 * x = 5x and 5 * 3 = 15.
Therefore, the factorised form of 5x + 15 is 5(x + 3).
Understanding the Process: The Distributive Property
The process of factorisation relies heavily on the distributive property of multiplication over addition. The distributive property states that a(b + c) = ab + ac. In our example:
5(x + 3) = 5 * x + 5 * 3 = 5x + 15
This shows that our factorised form is correct because expanding it gives us the original expression. This demonstrates the reversible nature of factorisation and expansion.
Factorisation with Negative Coefficients
Let's consider a slightly more complex scenario involving negative coefficients. What if the expression were -5x - 15?
1. Identify the Common Factor:
The common factor for -5x and -15 is still 5, but in this case, we'll factor out -5 to simplify the expression within the parentheses.
2. Factor Out the GCF (Including the Negative Sign):
-5x - 15 = -5(x + 3)
Notice that when we factor out -5, we get (x + 3) inside the parentheses. To verify this:
-5(x + 3) = -5 * x + (-5) * 3 = -5x - 15
This confirms that -5(x + 3) is indeed the correct factorisation. Always remember to consider the signs when identifying the GCF and factoring it out.
Expanding on Factorisation Techniques: Beyond the Basics
While the example of 5x + 15 showcases a simple case of factorisation, this technique can be applied to more intricate algebraic expressions. Let's explore some broader concepts:
-
Factorising Trinomials: Expressions like x² + 5x + 6 require a different approach. We look for two numbers that add up to the coefficient of the x term (5) and multiply to give the constant term (6). In this case, 2 and 3 satisfy this condition, leading to the factorisation (x + 2)(x + 3).
-
Difference of Squares: Expressions in the form a² - b² can be factored as (a + b)(a - b). For example, x² - 9 = (x + 3)(x - 3).
-
Grouping: For expressions with four or more terms, the grouping method is often employed. Terms are grouped together based on common factors, and then the common factor is factored out from each group.
-
Factor Theorem: This theorem is a more advanced technique used to find factors of polynomials of higher degree. It states that if P(a) = 0, then (x - a) is a factor of the polynomial P(x).
Applications of Factorisation in Mathematics and Beyond
Factorisation is not merely an abstract mathematical concept; it has wide-ranging applications:
-
Solving Quadratic Equations: Factorisation is a crucial step in solving quadratic equations of the form ax² + bx + c = 0. By factorising the quadratic expression, we can find the values of x that satisfy the equation.
-
Simplifying Algebraic Fractions: Factorisation allows us to simplify algebraic fractions by canceling common factors in the numerator and denominator.
-
Calculus: Factorisation is used extensively in calculus, particularly in differentiation and integration.
-
Physics and Engineering: Many physical phenomena and engineering designs are modeled using algebraic equations, and factorisation simplifies these equations for analysis and problem-solving.
-
Computer Science: Factorisation plays a crucial role in cryptography, specifically in algorithms for public-key cryptography.
Frequently Asked Questions (FAQ)
Q1: What happens if there is no common factor?
If there's no common factor between the terms, the expression is considered to be in its simplest form and cannot be factorised further using the GCF method. However, other factorisation techniques, such as those mentioned above, might still be applicable.
Q2: Can I factorise 5x + 15 in a different way?
While 5(x + 3) is the most simplified and commonly accepted factorisation, you could technically write it as other equivalent expressions. For example, you could write it as 1/2 * 10(x+3), but this isn't as simplified. The aim of factorisation is to find the simplest form, generally expressing the GCF as a single coefficient.
Q3: What if the expression involves more variables?
The same principles apply. Identify the greatest common factor of all terms, regardless of the number of variables involved. For example, in the expression 10xy + 15x, the GCF is 5x, resulting in the factorisation 5x(2y + 3).
Q4: Is there a quick way to check if my factorisation is correct?
Yes! Expand your factorised expression using the distributive property. If you get the original expression, your factorisation is correct.
Q5: What resources can I use to practice factorisation?
Numerous online resources, textbooks, and educational websites offer practice problems and tutorials on factorisation. Working through various examples will strengthen your understanding and skill.
Conclusion
Factorising the expression 5x + 15, resulting in 5(x + 3), is a seemingly simple task, but it reveals the fundamental principles of algebraic manipulation. This process, based on identifying the greatest common factor and applying the distributive property, forms the foundation for more complex factorisation techniques. Mastering factorisation is crucial not just for algebraic simplification, but also for solving equations, simplifying fractions, and tackling more advanced mathematical concepts in various fields of study. Remember to practice regularly to build proficiency and confidence in this essential algebraic skill. The more you practice, the faster and more intuitive the process will become.
Latest Posts
Latest Posts
-
Decimal Of 1 7
Sep 21, 2025
-
40 Of 3500
Sep 21, 2025
-
10 Of 14
Sep 21, 2025
-
Square Root 162
Sep 21, 2025
-
Mascotte Tokyo 2020
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Factorise 5x 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.