90 Of 400
interactiveleap
Sep 23, 2025 · 5 min read
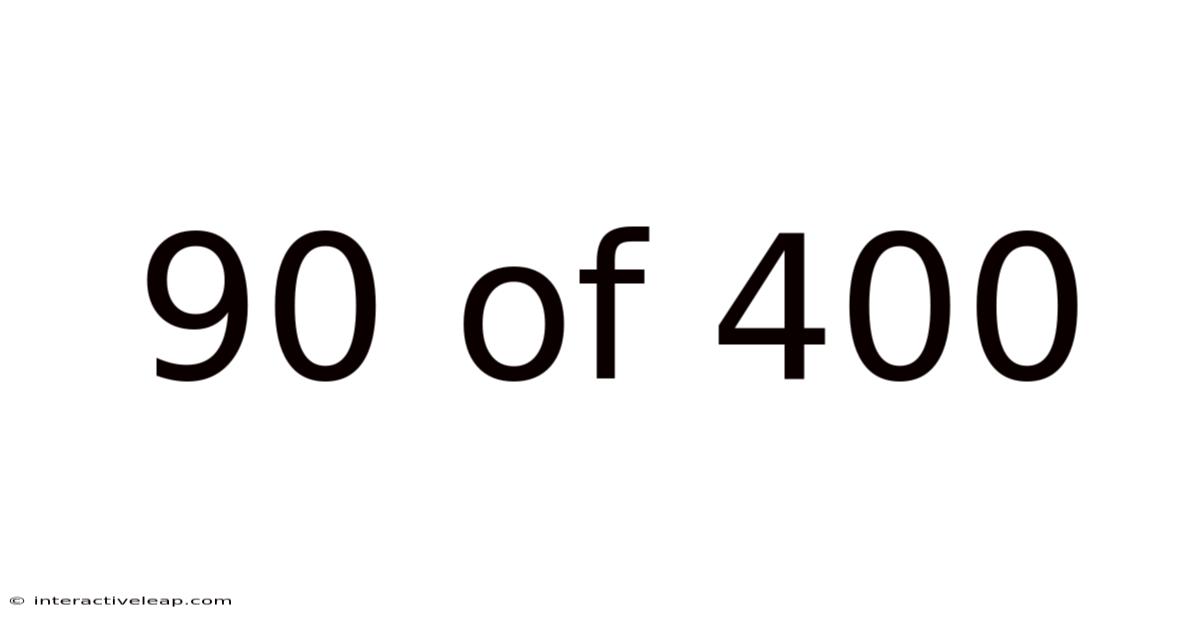
Table of Contents
Decoding 90 out of 400: Understanding Percentages, Fractions, and Their Applications
This article delves into the seemingly simple question: "What is 90 out of 400?" It goes beyond a simple percentage calculation to explore the underlying mathematical concepts, demonstrating various methods for solving similar problems and highlighting practical applications in everyday life. Understanding how to calculate and interpret fractions and percentages is crucial for various fields, from finance and statistics to everyday decision-making. We'll cover the basics, then explore more advanced applications and address frequently asked questions.
I. Understanding the Basics: Fractions and Percentages
The expression "90 out of 400" represents a fraction. In mathematical terms, it's written as 90/400. A fraction is a part of a whole. The top number (90) is the numerator, representing the part we're interested in. The bottom number (400) is the denominator, representing the total number of parts.
A percentage is simply a fraction expressed as a proportion of 100. To convert a fraction to a percentage, we divide the numerator by the denominator and multiply the result by 100. This gives us a value out of 100, allowing for easy comparison and understanding of proportions.
II. Calculating the Percentage: Step-by-Step Guide
Let's calculate the percentage represented by 90 out of 400:
-
Divide the numerator by the denominator: 90 ÷ 400 = 0.225
-
Multiply the result by 100: 0.225 × 100 = 22.5
Therefore, 90 out of 400 is 22.5%. This means that 90 represents 22.5% of the total of 400.
III. Alternative Calculation Methods
While the above method is straightforward, there are other ways to approach this calculation:
-
Simplifying the Fraction: Before converting to a percentage, we can simplify the fraction 90/400 by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 90 and 400 is 10. Dividing both the numerator and denominator by 10 simplifies the fraction to 9/40. Now, we can convert 9/40 to a percentage: 9 ÷ 40 = 0.225; 0.225 × 100 = 22.5%. This method can be helpful with larger numbers, making the division easier.
-
Using Proportions: We can set up a proportion to solve this. Let x represent the percentage: 90/400 = x/100. To solve for x, we cross-multiply: 400x = 9000. Then, divide both sides by 400: x = 22.5. This method emphasizes the relationship between the fraction and the percentage.
-
Using a Calculator: Most calculators have a percentage function that directly calculates the percentage of a number. Simply enter 90 ÷ 400 and then multiply by 100.
IV. Real-World Applications of Percentage Calculations
Understanding percentages is essential in numerous everyday situations:
-
Finance: Calculating interest rates, discounts, taxes, and investment returns all involve percentage calculations. For example, if a store offers a 20% discount on an item, you need to calculate the discounted price.
-
Statistics: Percentages are frequently used to represent data in graphs, charts, and reports. Understanding percentages helps interpret statistical information accurately. For instance, understanding the percentage of students who passed an exam or the percentage of people who voted for a particular candidate is crucial in interpreting election results or test scores.
-
Grades and Scores: Academic performance is often expressed as percentages. A student scoring 90 out of 100 on a test has achieved 90%.
-
Sales and Marketing: Sales figures are often represented as percentages of targets or previous periods. Companies use percentage increase or decrease in sales to track their success and growth.
-
Cooking and Baking: Recipes often require adjusting ingredient quantities based on the number of servings. Understanding percentages allows for accurate scaling of recipes. For example, if a recipe yields 400g of cake and you only want 90g, you need to calculate the appropriate proportions of each ingredient.
V. Expanding the Concept: Beyond 90 out of 400
The methods discussed above can be applied to any fraction. Let's consider some examples:
-
What is 150 out of 600? 150/600 = 0.25; 0.25 x 100 = 25%
-
What is 35 out of 280? 35/280 = 0.125; 0.125 x 100 = 12.5%
-
What is 72 out of 360? 72/360 = 0.2; 0.2 x 100 = 20%
Notice that in each case, we follow the same steps: divide the numerator by the denominator and multiply by 100. The ability to quickly and accurately calculate percentages is a valuable skill across various disciplines.
VI. Advanced Applications: Ratios and Proportions
The concept of "90 out of 400" can also be expressed as a ratio, which compares two quantities. The ratio of 90 to 400 can be written as 90:400 or 9:40 (after simplification). Understanding ratios is essential in various fields, particularly in chemistry and physics where the proportions of different elements or components are crucial.
Proportions are mathematical statements that equate two ratios. We used proportions earlier to solve for the percentage. Understanding and solving proportions are vital in scaling recipes, determining similar shapes, and solving numerous real-world problems.
VII. Frequently Asked Questions (FAQ)
-
What if the percentage doesn't come out to a whole number? Percentages can be decimals. For instance, 22.5% is a perfectly valid percentage.
-
Can I use a calculator for this? Absolutely! Calculators are a helpful tool for quickly performing these calculations.
-
What's the difference between a fraction, a ratio, and a percentage? A fraction represents a part of a whole. A ratio compares two quantities. A percentage is a fraction expressed as a proportion of 100.
-
How can I improve my understanding of percentages? Practice is key! Try working through various examples and applying percentage calculations to real-world scenarios. Online resources and educational materials can provide additional support.
VIII. Conclusion: Mastering Percentages for a Brighter Future
Understanding how to calculate and interpret "90 out of 400" (or any similar fraction) is more than just a mathematical exercise; it's a fundamental skill with far-reaching applications. From managing personal finances and interpreting data to excelling in academic and professional settings, the ability to work comfortably with fractions and percentages is an invaluable asset. By mastering these concepts, you equip yourself with the tools to navigate a complex world with greater confidence and understanding. The ability to perform these calculations efficiently is crucial for success in many areas of life. Continue to practice, explore various applications, and remember the core principles discussed here.
Latest Posts
Latest Posts
-
40 Of 2200
Sep 23, 2025
-
Philosophy Of Psychology
Sep 23, 2025
-
5 12 X 6
Sep 23, 2025
-
Sodium Sulfide Formula
Sep 23, 2025
-
The Flower Carrier
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 90 Of 400 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.