5/12 X 6
interactiveleap
Sep 23, 2025 · 6 min read
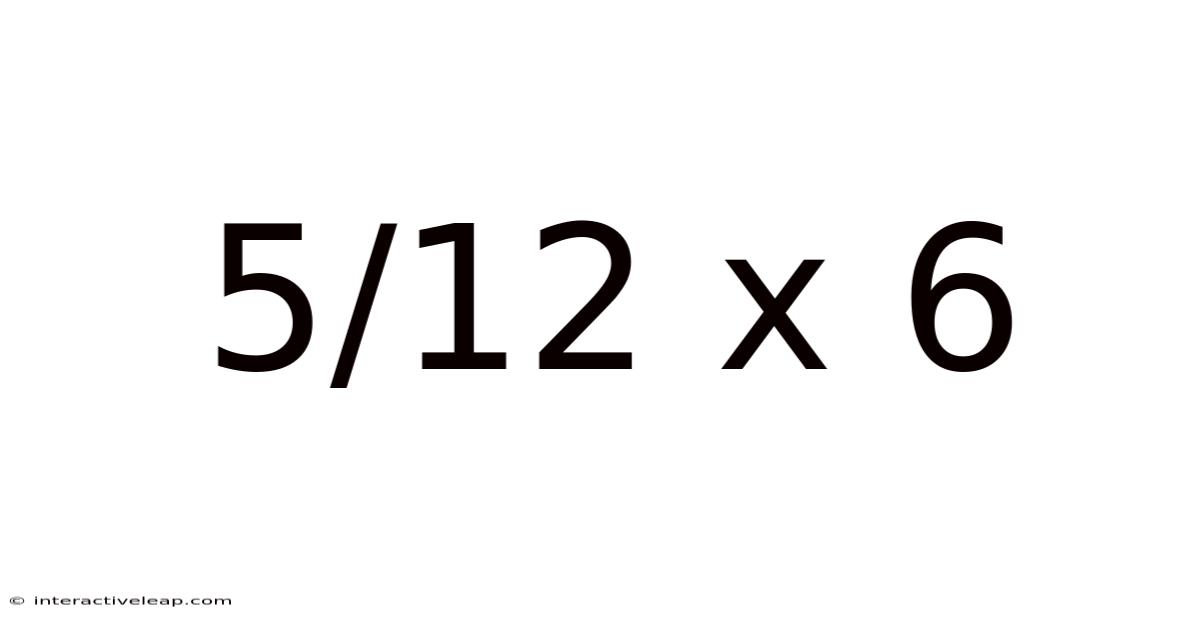
Table of Contents
Decoding 5/12 x 6: A Deep Dive into Fraction Multiplication
This article explores the seemingly simple mathematical problem of 5/12 x 6, delving beyond the basic calculation to uncover the underlying principles and practical applications of fraction multiplication. We'll break down the process step-by-step, explore the mathematical concepts involved, and address common questions and misconceptions. By the end, you'll not only understand how to solve this specific problem but also gain a solid foundation in multiplying fractions with whole numbers. This comprehensive guide will serve as a valuable resource for students, educators, and anyone seeking to refresh their understanding of fractions.
Understanding the Problem: 5/12 x 6
The problem, 5/12 x 6, involves multiplying a fraction (5/12) by a whole number (6). This type of calculation is fundamental in various mathematical applications, from everyday tasks like baking and cooking to more complex scientific and engineering problems. Understanding this seemingly simple problem unlocks a broader understanding of fractional arithmetic.
Step-by-Step Solution:
There are several ways to approach this multiplication problem. Let's examine two common methods:
Method 1: Converting the Whole Number to a Fraction
This method involves rewriting the whole number 6 as a fraction. Any whole number can be expressed as a fraction by placing it over 1. Therefore, 6 becomes 6/1.
-
Rewrite the problem: The problem now becomes (5/12) x (6/1).
-
Multiply the numerators: Multiply the top numbers (numerators) together: 5 x 6 = 30.
-
Multiply the denominators: Multiply the bottom numbers (denominators) together: 12 x 1 = 12.
-
Simplify the resulting fraction: The result is 30/12. This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 30 and 12 is 6. Divide both the numerator and denominator by 6: 30 ÷ 6 = 5 and 12 ÷ 6 = 2.
-
Final answer: The simplified fraction is 5/2. This can be further expressed as a mixed number: 2 ½.
Method 2: Canceling Before Multiplication
This method, often preferred for its efficiency, involves simplifying the fractions before multiplying. This reduces the size of the numbers involved, making the calculation easier and minimizing the need for simplification at the end.
-
Rewrite the problem: We have (5/12) x 6. Remember that 6 can be written as 6/1.
-
Identify common factors: Notice that the denominator 12 and the numerator 6 share a common factor of 6. We can simplify before multiplying.
-
Cancel the common factor: Divide both 12 and 6 by their greatest common divisor, which is 6. This simplifies the expression to (5/2) x 1.
-
Multiply the remaining numbers: Multiply the numerator 5 by 1, and the denominator 2 by 1.
-
Final answer: The result is 5/2, which is equivalent to 2 ½.
Mathematical Concepts Involved:
This simple problem highlights several crucial mathematical concepts:
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates the total number of equal parts, while the numerator indicates how many of those parts are being considered.
-
Multiplication of Fractions: Multiplying fractions involves multiplying the numerators together to get the new numerator and multiplying the denominators together to get the new denominator.
-
Simplifying Fractions: Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). This doesn't change the value of the fraction, just its representation.
-
Equivalent Fractions: Different fractions can represent the same value. For example, 30/12, 15/6, 5/2, and 2 ½ are all equivalent fractions.
-
Whole Numbers as Fractions: Any whole number can be expressed as a fraction by placing it over 1. This allows us to apply the rules of fraction multiplication consistently.
-
Greatest Common Divisor (GCD): The GCD is the largest number that divides evenly into two or more numbers. Finding the GCD is crucial for simplifying fractions.
Practical Applications:
The ability to multiply fractions with whole numbers is essential in many real-world situations:
-
Cooking and Baking: Recipes often involve fractional amounts of ingredients. Multiplying fractions by whole numbers is necessary when scaling a recipe up or down. For instance, if a recipe calls for 5/12 of a cup of flour and you want to triple the recipe, you'll need to calculate 5/12 x 3.
-
Construction and Engineering: Measurements in construction and engineering often involve fractions. Multiplying fractions helps in calculations related to distances, volumes, and areas.
-
Finance: Calculations involving percentages and interest often involve fractions. Understanding fraction multiplication is key for managing personal finances or understanding financial reports.
-
Data Analysis: Many data analysis tasks involve dealing with proportions and ratios, which are often expressed as fractions. Multiplying fractions allows for the manipulation and interpretation of data.
Frequently Asked Questions (FAQ):
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes them easier to understand and work with. It also makes it easier to compare fractions and to see relationships between them.
Q: What if I forget to simplify the fraction after multiplying?
A: While your answer will still be mathematically correct, it won't be in its simplest form. This can make further calculations more difficult and may lead to errors. Always aim to simplify your fractions to their lowest terms.
Q: Can I multiply the whole number by the numerator and then divide by the denominator?
A: Yes, this is a valid method. For the example 5/12 x 6, you can multiply 5 x 6 = 30, then divide 30 by 12, giving you 5/2 or 2 ½. This method is essentially a combination of the steps we've already discussed.
Q: What if the whole number and the denominator have no common factors?
A: In that case, you simply multiply the numerators and denominators directly, and then simplify the resulting fraction if necessary. The canceling method is still beneficial because it makes the multiplication simpler, even if it doesn't lead to any cancellation.
Q: Are there other ways to represent the answer, 5/2?
A: Yes, the answer 5/2 can be represented as an improper fraction (where the numerator is greater than the denominator), or as a mixed number (a whole number and a fraction). Both 5/2 and 2 ½ represent the same value. The best representation depends on the context of the problem.
Conclusion:
Solving 5/12 x 6, while seemingly straightforward, provides a valuable opportunity to revisit and solidify our understanding of fractional arithmetic. Mastering fraction multiplication is crucial for success in various mathematical applications, and understanding the underlying concepts – including fractions, simplification, and equivalent fractions – empowers you to tackle more complex problems with confidence. Remember the importance of simplification and the flexibility offered by different solution methods. The ultimate goal is not just to get the right answer but also to develop a deep understanding of the principles involved. This understanding will be invaluable as you progress to more advanced mathematical concepts.
Latest Posts
Latest Posts
-
1 78meters In Feet
Sep 23, 2025
-
0 7 As Fraction
Sep 23, 2025
-
Victorian Architecture Uk
Sep 23, 2025
-
Levers And Linkages
Sep 23, 2025
-
Milliseconds To Microseconds
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5/12 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.