9 X 27
interactiveleap
Sep 22, 2025 · 6 min read
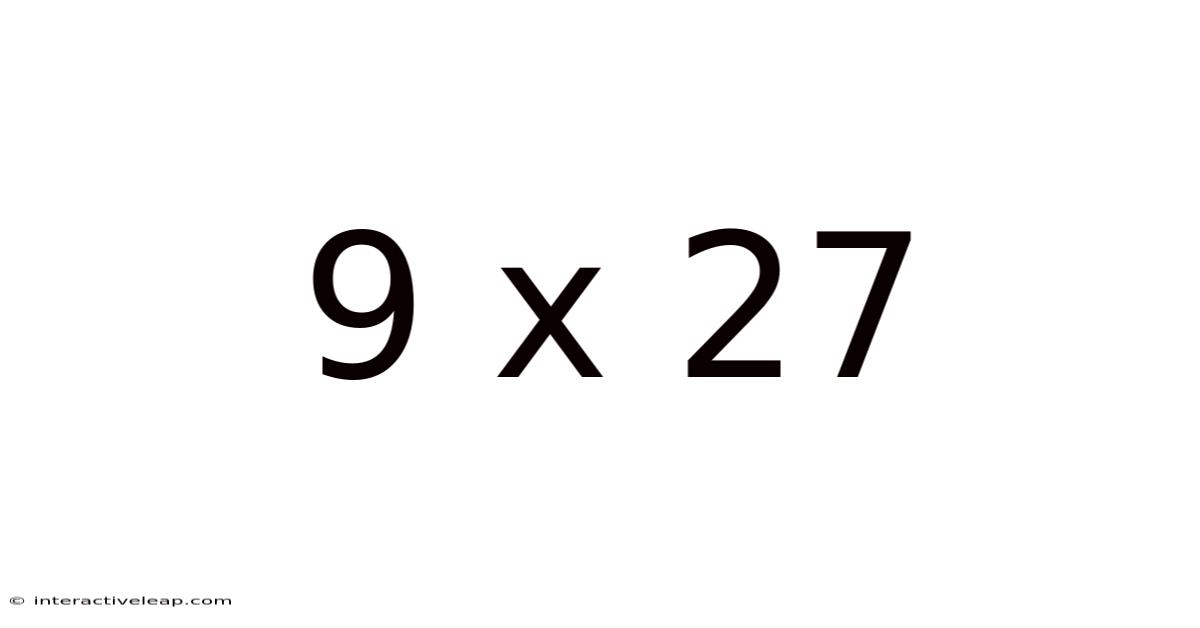
Table of Contents
Unveiling the Wonders of 9 x 27: A Deep Dive into Multiplication and Beyond
The seemingly simple multiplication problem, 9 x 27, offers a gateway to explore a fascinating world of mathematical concepts, problem-solving strategies, and real-world applications. This article delves deep into this seemingly basic calculation, uncovering its hidden depths and demonstrating its relevance across various fields. We will not only solve the equation but also examine the underlying principles of multiplication, explore different methods of calculation, and discuss how this seemingly simple operation connects to more complex mathematical ideas. This exploration is perfect for anyone wanting to brush up on their multiplication skills, delve into the beauty of mathematics, or simply satisfy their curiosity about the number 243.
Understanding the Fundamentals: What is Multiplication?
Before we tackle 9 x 27, let's revisit the fundamental concept of multiplication. Multiplication is essentially a shortcut for repeated addition. When we say 9 x 27, we are essentially asking: "What is the sum of nine twenty-sevens?" Or, equivalently, "What is the result of adding 27 to itself nine times?" Understanding this foundational principle helps to visualize the operation and grasp its meaning beyond rote memorization.
Methods for Solving 9 x 27
There are several methods to calculate 9 x 27, ranging from basic multiplication techniques to more advanced strategies. Let's explore a few:
1. Traditional Multiplication Method:
This is the standard method taught in schools. It involves multiplying the ones digit of 27 (7) by 9, then the tens digit (2) by 9, and finally adding the results together:
- 9 x 7 = 63 (write down 3, carry-over 6)
- 9 x 2 = 18 + 6 (carry-over) = 24
- Therefore, 9 x 27 = 243
2. Distributive Property:
The distributive property allows us to break down the multiplication into smaller, more manageable parts. We can rewrite 27 as (20 + 7), and then apply the distributive property:
9 x (20 + 7) = (9 x 20) + (9 x 7) = 180 + 63 = 243
3. Using Multiplication Tables:
If you have memorized your multiplication tables, this problem becomes straightforward. Knowing that 9 x 20 = 180 and 9 x 7 = 63 allows for a quick calculation: 180 + 63 = 243
4. Mental Math Techniques:
With practice, you can perform this calculation mentally. One strategy involves thinking of 9 as (10 - 1):
10 x 27 = 270 270 - 27 = 243
The Number 243: A Deeper Look
The result of 9 x 27, 243, is itself a fascinating number. Let's explore some of its properties:
-
Factors: The factors of 243 are 1, 3, 9, 27, 81, and 243. Notice the pattern of powers of 3 (3<sup>1</sup>, 3<sup>2</sup>, 3<sup>3</sup>, 3<sup>4</sup>, 3<sup>5</sup>). This reveals that 243 is a power of 3, specifically 3<sup>5</sup>.
-
Prime Factorization: The prime factorization of 243 is 3 x 3 x 3 x 3 x 3, or 3<sup>5</sup>. This highlights its unique relationship to the prime number 3.
-
Divisibility Rules: 243 is divisible by 3 and 9, consistent with the divisibility rules for these numbers (the sum of digits is divisible by 3 and 9).
-
Geometric Significance: In geometry, 243 could represent the number of unit cubes in a larger cube, or the volume of a three-dimensional shape.
Real-World Applications: Where do we use 9 x 27?
While this particular multiplication problem might not appear explicitly in everyday life, the principles and techniques used to solve it are invaluable in countless situations. Here are a few examples:
-
Calculating Costs: Imagine you're buying 9 items that cost $27 each. Understanding 9 x 27 allows you to quickly calculate the total cost.
-
Area Calculation: If you have a rectangular area with dimensions of 9 units and 27 units, the calculation 9 x 27 gives you the total area.
-
Engineering and Design: In various engineering and design projects, multiplication is crucial for calculations related to dimensions, quantities, and material requirements. The ability to perform quick and accurate multiplication is essential.
-
Data Analysis: In the realm of data analysis and statistics, multiplication is frequently used in various calculations, including calculating probabilities, averages, and proportions.
Expanding the Horizons: Connecting to Advanced Concepts
The seemingly simple problem of 9 x 27 can serve as a springboard to explore more complex mathematical concepts:
-
Algebra: The equation can be represented algebraically as x = 9 * 27, where x represents the unknown product. This simple equation introduces the concept of variables and solving for unknowns.
-
Exponents and Powers: As we saw, 243 is 3<sup>5</sup>. This introduces the concept of exponents and their relationship to multiplication. Understanding exponents is crucial for many advanced mathematical concepts.
-
Number Theory: The study of 243’s factors and prime factorization touches upon fundamental concepts in number theory, such as prime numbers, composite numbers, and the unique prime factorization theorem.
-
Calculus: While not directly apparent, the principles of multiplication are foundational to calculus. Differentiation and integration, fundamental concepts in calculus, build upon basic arithmetic operations.
Frequently Asked Questions (FAQ)
-
Q: What are some common mistakes students make when solving 9 x 27?
- A: Common mistakes include errors in carrying over digits during the traditional multiplication method, misapplication of the distributive property, and inaccurate use of mental math techniques. Careful attention to detail and practice are key to avoiding these errors.
-
Q: Are there any tricks to remember the multiplication fact 9 x 27?
- A: While there isn't a specific trick unique to this multiplication fact, memorizing multiplication tables or using mental math strategies as discussed earlier can make recalling the answer easier.
-
Q: How can I improve my multiplication skills?
- A: Consistent practice is crucial. Use flashcards, online games, and work through multiplication problems regularly. Start with easier problems and gradually increase the difficulty. Understanding the underlying principles of multiplication, as explained above, will also greatly assist.
-
Q: Is there a faster way to calculate 9 x 27 than the traditional method?
- A: Yes, the distributive property and mental math techniques (like using 10 - 1) can often be faster than the traditional method, especially with practice.
Conclusion: More Than Just a Calculation
The seemingly simple equation 9 x 27 is far more than just a multiplication problem. It's a gateway to exploring fundamental mathematical concepts, practicing various calculation methods, and appreciating the interconnectedness of seemingly disparate mathematical fields. By understanding the principles behind this calculation and exploring its deeper implications, we gain a richer understanding of mathematics and its relevance to the world around us. The journey from a simple multiplication problem to the exploration of prime factorization, exponents, and real-world applications highlights the beauty and power of mathematics – a subject that is both challenging and endlessly rewarding. The next time you encounter a seemingly straightforward mathematical problem, remember the depth and breadth of understanding that can be unlocked by a thorough exploration. So, keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
40 Of 230
Sep 22, 2025
-
1 2 Liters Ml
Sep 22, 2025
-
18cn To Inches
Sep 22, 2025
-
0 73 In Percentage
Sep 22, 2025
-
Calcium Bromide Formula
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 9 X 27 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.