40 Of 230
interactiveleap
Sep 22, 2025 · 6 min read
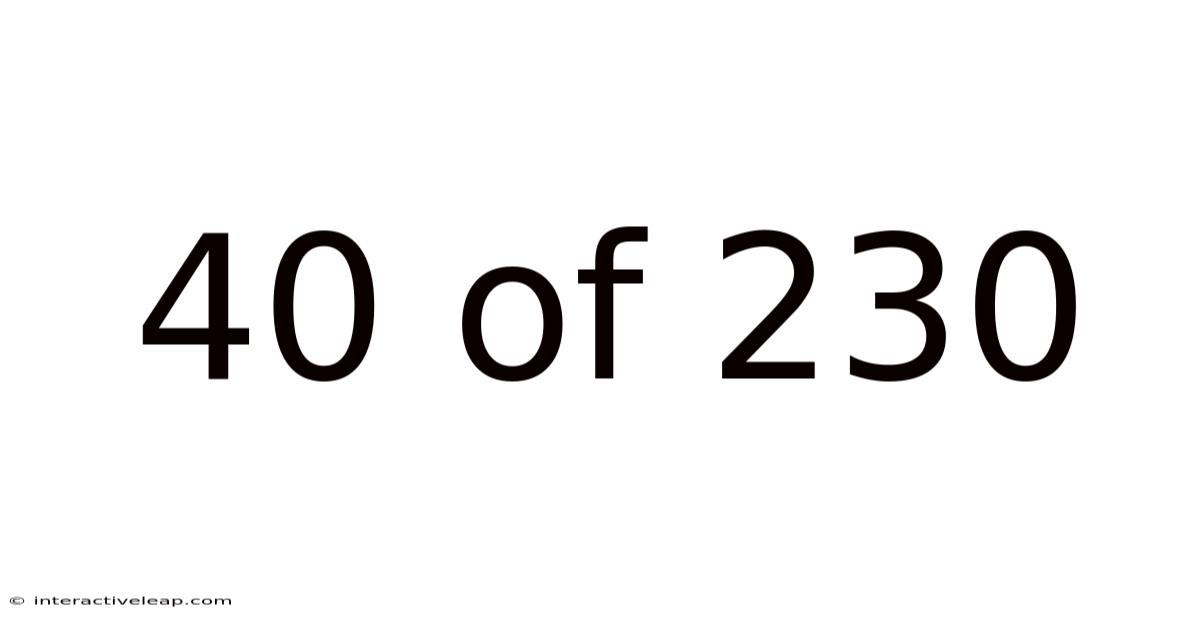
Table of Contents
Decoding the Fraction: Understanding 40/230 and its Implications
The seemingly simple fraction 40/230 might appear insignificant at first glance. However, understanding its implications requires delving into the world of fractions, simplification, percentages, and their applications in various fields. This article will comprehensively explore 40/230, guiding you through its simplification, its percentage representation, and the practical contexts where such fractions arise. We'll also address common misconceptions and frequently asked questions.
Introduction: The Significance of Fractional Understanding
Fractions are fundamental mathematical concepts representing parts of a whole. They play a crucial role in numerous areas, from everyday tasks like cooking and measuring to complex calculations in engineering and finance. Understanding fractions like 40/230 is not merely about performing calculations; it's about developing a deeper appreciation for proportional relationships and the ability to interpret data accurately. This article aims to empower you with the knowledge and skills to confidently handle and interpret fractions like 40/230.
1. Simplifying 40/230: Finding the Greatest Common Divisor (GCD)
Before delving into further analysis, the first step is to simplify the fraction 40/230 to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (40) and the denominator (230). The GCD is the largest number that divides both numbers without leaving a remainder.
To find the GCD of 40 and 230, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- Prime factorization of 40: 2 x 2 x 2 x 5 = 2³ x 5
- Prime factorization of 230: 2 x 5 x 23
By comparing the prime factorizations, we can see that the common factors are 2 and 5. Therefore, the GCD of 40 and 230 is 2 x 5 = 10.
Now, we divide both the numerator and the denominator by the GCD:
40 ÷ 10 = 4 230 ÷ 10 = 23
Therefore, the simplified form of 40/230 is 4/23. This simplified fraction is much easier to work with and represents the same proportional relationship as the original fraction.
2. Converting 4/23 to a Percentage
Converting a fraction to a percentage provides a more intuitive understanding of its relative size. To convert 4/23 to a percentage, we perform the following calculation:
(4 ÷ 23) x 100%
This calculation results in approximately 17.39%. This means that 40/230, or its simplified equivalent 4/23, represents approximately 17.39% of the whole.
3. Practical Applications of 40/230 (or 4/23)
The fraction 40/230, and its simplified form 4/23, can represent various real-world scenarios. Here are some examples:
-
Test Scores: Imagine a student scoring 40 out of 230 points on a test. Their score would be 4/23 or approximately 17.39%. This allows for easy comparison with other students' scores.
-
Surveys and Polls: If 40 out of 230 respondents answered "yes" to a particular question in a survey, the fraction 4/23 (17.39%) represents the proportion of positive responses.
-
Inventory Management: A warehouse might have 40 units of a particular item out of a total stock of 230 units. The fraction 4/23 indicates the proportion of that specific item in the total inventory.
-
Financial Calculations: In finance, this fraction could represent a portion of a portfolio, a percentage of a loan repaid, or a share of a company's profit.
-
Scientific Measurements: In scientific experiments, ratios and proportions are frequently expressed as fractions. 4/23 could represent a concentration of a substance, a ratio of reactants in a chemical reaction, or a probability in statistical analysis.
4. Understanding the Concept of Proportionality
Fractions are inherently linked to the concept of proportionality. The fraction 40/230 (or 4/23) demonstrates a proportional relationship between two quantities. It shows the relative size of one quantity compared to another. This understanding of proportionality is crucial in various fields, including:
-
Scaling: Enlarging or reducing images, maps, or blueprints relies heavily on proportional relationships.
-
Mixing Ratios: In cooking, painting, or chemistry, accurate mixing ratios are essential for achieving desired results.
-
Similar Triangles: In geometry, similar triangles exhibit proportional relationships between their corresponding sides.
5. Addressing Common Misconceptions
Several common misconceptions surround fractions:
-
Ignoring Simplification: Failing to simplify a fraction can lead to unnecessary complexity in calculations and interpretations. Always simplify to its lowest terms for easier handling.
-
Confusing Numerator and Denominator: The numerator represents the part, while the denominator represents the whole. Confusing these two leads to incorrect calculations and interpretations.
-
Difficulty with Improper Fractions: An improper fraction is where the numerator is larger than the denominator (e.g., 23/4). Understanding how to convert improper fractions to mixed numbers (e.g., 5 ¾) is essential for accurate calculations.
-
Misinterpreting Percentages: Percentages are simply fractions expressed as a proportion of 100. Understanding the relationship between fractions and percentages is critical for accurate interpretations.
6. Frequently Asked Questions (FAQ)
-
Q: How do I add or subtract fractions? A: To add or subtract fractions, they must have a common denominator. If they don't, find the least common multiple (LCM) and convert the fractions accordingly. Then, add or subtract the numerators and keep the denominator the same.
-
Q: How do I multiply fractions? A: Multiply the numerators together and multiply the denominators together. Simplify the resulting fraction if possible.
-
Q: How do I divide fractions? A: To divide a fraction by another fraction, invert the second fraction (reciprocal) and then multiply.
-
Q: What is a mixed number? A: A mixed number consists of a whole number and a fraction (e.g., 2 ¾).
-
Q: How do I convert an improper fraction to a mixed number? A: Divide the numerator by the denominator. The quotient is the whole number part, and the remainder is the numerator of the fractional part, with the denominator remaining the same.
-
Q: How do I convert a mixed number to an improper fraction? A: Multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator remains the same.
7. Conclusion: Mastering Fractions – A Lifelong Skill
Understanding fractions is a crucial skill that extends far beyond the classroom. Whether you're calculating percentages, interpreting data, or solving real-world problems, a solid grasp of fractions is invaluable. By breaking down the seemingly simple fraction 40/230, we've explored its simplification, percentage representation, practical applications, and the broader concept of proportionality. Mastering fractions empowers you to approach numerical challenges with confidence and analytical precision, making it a lifelong skill worth cultivating. The ability to dissect and comprehend fractions like 40/230 is not just about mathematical proficiency; it's about developing critical thinking skills that are applicable across numerous aspects of life. This deep understanding allows for a more nuanced interpretation of data, a more accurate approach to problem-solving, and a greater appreciation for the interconnectedness of mathematical concepts in the world around us.
Latest Posts
Latest Posts
-
6 7kg In Stone
Sep 22, 2025
-
44lbs To Kg
Sep 22, 2025
-
48 100 Simplified
Sep 22, 2025
-
30 Of 1900
Sep 22, 2025
-
Hms Warrior Photos
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 40 Of 230 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.