9 4 X
interactiveleap
Sep 19, 2025 · 6 min read
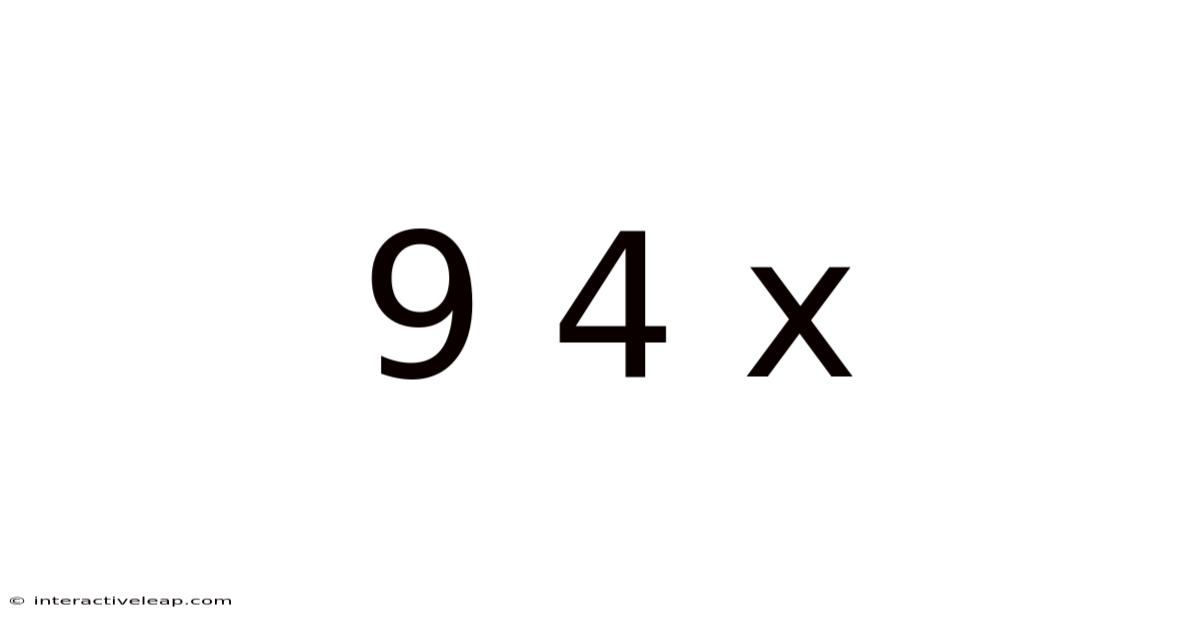
Table of Contents
Decoding 9/4x: A Comprehensive Exploration of its Mathematical Significance and Applications
The expression "9/4x" might seem simple at first glance, but it harbors a rich tapestry of mathematical concepts and practical applications that extend far beyond basic arithmetic. This seemingly straightforward fractional expression opens doors to understanding fundamental algebraic principles, their role in problem-solving, and their relevance in diverse fields. This article will dissect 9/4x, exploring its nuances, clarifying potential ambiguities, and demonstrating its use in various contexts.
Understanding the Fundamentals: Order of Operations (PEMDAS/BODMAS)
Before diving into the intricacies of 9/4x, it's crucial to establish a solid foundation in the order of operations. This set of rules dictates the sequence in which mathematical operations should be performed to ensure consistency and accuracy in calculations. These rules are often summarized by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms convey the same fundamental principle:
- Parentheses/Brackets: Operations within parentheses or brackets are always performed first.
- Exponents/Orders: Exponents (powers) are calculated next.
- Multiplication and Division: Multiplication and division have equal precedence and are performed from left to right.
- Addition and Subtraction: Addition and subtraction also have equal precedence and are performed from left to right.
The order of operations is paramount when dealing with expressions like 9/4x. The absence of parentheses creates a potential source of confusion, which we will address in detail.
Interpreting 9/4x: The Ambiguity and its Resolution
The primary challenge with 9/4x lies in the implicit multiplication between 4 and x. Is it (9/4) * x or 9 / (4x)? The absence of explicit parentheses creates ambiguity. To avoid this ambiguity, mathematicians and programmers generally adopt a convention:
- Implicit Multiplication Precedence: Implicit multiplication (multiplication without a symbol) often takes precedence over explicit division. Therefore, 9/4x is generally interpreted as (9/4) * x.
This convention ensures clarity and consistency in calculations. However, it's always best practice to use parentheses to remove any doubt. Writing (9/4)x or 9/(4x) clarifies the intended operation, preventing misinterpretations.
Solving (9/4)x: A Step-by-Step Approach
Let's assume the standard interpretation of 9/4x as (9/4)x. To solve this expression, we simply perform the division first and then the multiplication:
- Division: 9 divided by 4 equals 2.25 (or 9/4 = 2.25).
- Multiplication: Multiply the result (2.25) by x. This gives us 2.25x.
Therefore, if we assume the standard interpretation, 9/4x simplifies to 2.25x. This expression represents a linear relationship where the value is directly proportional to x.
Solving 9/(4x): An Alternate Interpretation
Now, let's consider the alternative interpretation: 9/(4x). In this case, the denominator (4x) is treated as a single unit. The solution would involve:
- Multiplication in the Denominator: First, multiply 4 by x (4x).
- Division: Then, divide 9 by the result (4x). This gives us 9/(4x).
This expression, 9/(4x), is also a valid interpretation, but it represents a different mathematical relationship than (9/4)x. This highlights the importance of clear notation and the use of parentheses to eliminate ambiguity.
Applications of 9/4x and Related Expressions in Various Fields
Although seemingly simple, expressions like 9/4x have far-reaching applications in various fields:
-
Physics and Engineering: Fractional expressions are ubiquitous in physics and engineering formulas. For example, calculating acceleration (a = (v_f - v_i)/t), force (F = ma), or resistance in a circuit often involves fractions and variables similar to 9/4x. Replacing 'x' with specific values representing physical quantities allows us to calculate the desired outcome.
-
Chemistry and Biochemistry: Stoichiometry, the study of quantitative relationships in chemical reactions, relies heavily on fractional calculations. The ratio of reactants and products in a chemical reaction can often be expressed using fractions, leading to expressions similar to 9/4x where 'x' might represent the amount of a specific reactant.
-
Economics and Finance: Economic models often utilize linear equations to represent relationships between variables. An expression like 9/4x could represent a simplified model of cost, profit, or growth, where x is a factor such as production quantity or investment amount.
-
Computer Science and Programming: In programming, expressions similar to 9/4x are frequently encountered when dealing with calculations, loops, and algorithms. Understanding the order of operations is crucial for writing efficient and error-free code.
-
Statistics and Data Analysis: Statistical calculations often involve ratios and fractions. Expressions similar to 9/4x can arise in calculations involving proportions, probabilities, or sampling distributions. Here, 'x' might represent a sample size or a particular data point.
Beyond the Basics: Expanding on Fractional Expressions
The expression 9/4x serves as a stepping stone to understanding more complex fractional expressions. Consider these examples:
- (9/4x) + 5: This expression adds a constant term to the basic 9/4x. Understanding how to combine fractional and whole numbers is essential in solving algebraic equations.
- (9/4x) * (2/3y): This showcases multiplying two fractional expressions involving multiple variables. Mastering this skill is crucial for solving more complex equations and problems.
- (9/4x)^2: This demonstrates how to apply exponents to fractional expressions. Understanding the rules of exponents is crucial when dealing with more advanced mathematical concepts.
Frequently Asked Questions (FAQs)
Q: What is the difference between 9/4x and 9/(4x)?
A: The difference lies in the order of operations. 9/4x is generally interpreted as (9/4) * x, while 9/(4x) treats (4x) as a single entity in the denominator. Always use parentheses to clarify your intended meaning.
Q: Can 9/4x be simplified further?
A: If interpreted as (9/4)x, it can be simplified to 2.25x. If interpreted as 9/(4x), it cannot be simplified further unless a value is given for x.
Q: What if x equals 0?
A: If x equals 0, then both interpretations (9/4)x and 9/(4x) would result in 0, but 9/(4x) is undefined because division by zero is undefined in mathematics.
Q: How can I avoid errors when dealing with expressions like 9/4x?
A: Always use parentheses to explicitly define the order of operations. Never rely on implicit multiplication rules alone, as they can lead to ambiguities and errors.
Conclusion: Mastering the Nuances of Fractional Expressions
The seemingly straightforward expression 9/4x unveils a wealth of mathematical concepts and practical applications. Understanding the order of operations, interpreting implicit multiplication, and recognizing the potential ambiguities are key to correctly solving and applying this type of expression. This exploration extends beyond simple arithmetic and highlights the importance of clear notation, meticulous calculation, and the practical relevance of seemingly basic mathematical concepts in various fields of study and application. By mastering the nuances of expressions like 9/4x, you build a strong foundation for tackling more complex mathematical problems and applications. Remember, mathematical precision is paramount, and clarifying your expressions through consistent use of parentheses is a crucial element of success.
Latest Posts
Latest Posts
-
25 Of 140000
Sep 20, 2025
-
Examen In French
Sep 20, 2025
-
78inch To Feet
Sep 20, 2025
-
250ibs To Kg
Sep 20, 2025
-
Assumed Identity Crossword
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 9 4 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.