25 Of 140000
interactiveleap
Sep 20, 2025 · 5 min read
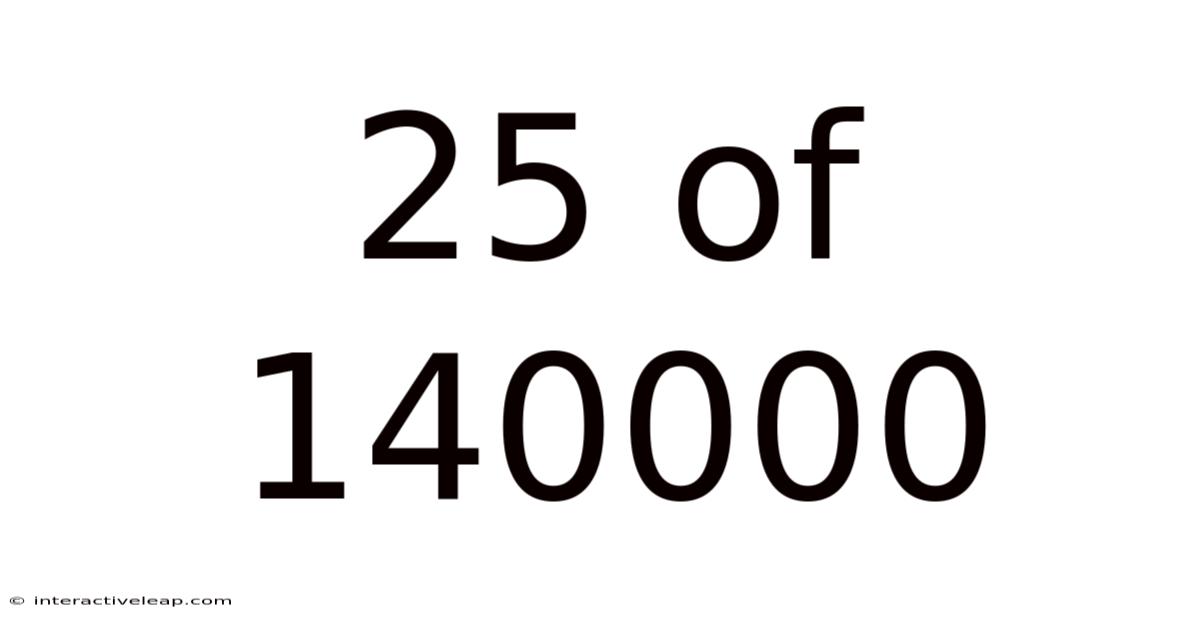
Table of Contents
Unveiling the Significance of 25 out of 140,000: A Deep Dive into Proportions and Probabilities
The seemingly insignificant fraction, 25 out of 140,000, hides a wealth of mathematical and statistical implications. Understanding its significance requires exploring concepts like proportions, percentages, probabilities, and the context in which this ratio appears. This article will delve into the meaning of this fraction, its representation, and its practical applications, aiming to illuminate its importance beyond a simple numerical expression. We will explore how understanding this seemingly small number can provide valuable insights across various fields.
Understanding the Basics: Proportions and Percentages
Before diving into the specifics of 25 out of 140,000, let's revisit fundamental concepts. A proportion simply represents the relationship between two quantities. In our case, the proportion is 25:140,000. This can be expressed as a fraction (25/140,000), a decimal (approximately 0.00017857), or a percentage (approximately 0.017857%).
Calculating the percentage provides a more intuitive understanding. To find the percentage, we divide the smaller number (25) by the larger number (140,000) and then multiply by 100:
(25/140,000) * 100 ≈ 0.0179%
This means that 25 represents approximately 0.0179% of 140,000. While this seems small, the context is crucial in determining its actual significance.
Context is King: The Importance of the Application
The significance of 25 out of 140,000 dramatically changes depending on the context. Let's consider several scenarios:
-
Scenario 1: Medical Trials: If 25 out of 140,000 participants in a clinical trial experienced a serious side effect from a new drug, this represents a low but potentially concerning incidence rate. Further investigation into the nature of the side effect and potential risk factors would be necessary. Statistical analysis would determine if this rate is significantly higher than the expected background rate of such side effects.
-
Scenario 2: Manufacturing Defects: If 25 out of 140,000 manufactured items are defective, this represents a relatively low defect rate (approximately 0.018%). While seemingly acceptable, the cost of repairing or replacing those 25 defective items, and the potential for future defects, needs to be considered in terms of production efficiency and quality control.
-
Scenario 3: Lottery Wins: If 25 people out of 140,000 lottery ticket holders win a prize, this reflects a low probability of winning. This helps to illustrate the odds associated with the lottery and can inform the decision-making process of potential participants.
-
Scenario 4: Population Statistics: If 25 out of 140,000 individuals in a specific demographic group exhibit a particular characteristic, this could signify a low prevalence rate. However, depending on the characteristic, this could still be statistically significant and warrant further investigation or intervention.
-
Scenario 5: Scientific Research: In scientific research, particularly in fields like astronomy or particle physics, observing 25 instances of a rare phenomenon out of 140,000 observations could be considered a significant finding, potentially leading to further investigations and the development of new theories or models.
Statistical Significance and Hypothesis Testing
In many contexts, determining the significance of 25 out of 140,000 requires statistical analysis. This involves employing statistical tests, such as chi-square tests or z-tests, to determine if the observed proportion is statistically different from an expected or null hypothesis. For example:
- Null hypothesis: The proportion of defective items is less than or equal to a predefined threshold.
- Alternative hypothesis: The proportion of defective items exceeds the predefined threshold.
The statistical test would determine the probability (p-value) of observing the data (25 defective items out of 140,000) if the null hypothesis were true. A low p-value (typically less than 0.05) would suggest that the null hypothesis should be rejected, indicating that the observed proportion is statistically significant.
Probability and Odds
From a probability perspective, the odds of a specific event occurring can be expressed as the ratio of favorable outcomes to unfavorable outcomes. In our example, if we consider the event of selecting one of the 25 items out of 140,000, the probability of success is:
25/140,000 ≈ 0.000179
This represents a very low probability. However, it's crucial to remember that probability doesn't predict certainty; it expresses the likelihood of an event happening.
Visual Representation and Data Presentation
Effectively communicating the proportion 25 out of 140,000 often necessitates visual aids. A bar chart, pie chart, or even a simple table can help illustrate the relationship between the two numbers. A visually compelling representation can make the information more accessible and easier to grasp for a wider audience. The choice of visualization depends on the context and the intended audience.
Applications in Different Fields
The concept of 25 out of 140,000 finds applications across numerous disciplines:
- Medicine: Analyzing disease prevalence, drug efficacy, and side effect rates.
- Engineering: Assessing product defect rates, failure rates, and reliability.
- Finance: Evaluating investment risks, portfolio performance, and fraud detection.
- Social Sciences: Studying survey responses, analyzing demographic data, and measuring social phenomena.
- Environmental Science: Monitoring pollution levels, studying species population dynamics, and assessing environmental impact.
Frequently Asked Questions (FAQ)
Q1: How do I calculate the percentage from a ratio like 25/140,000?
A1: Divide the numerator (25) by the denominator (140,000) and multiply the result by 100. (25/140,000) * 100 ≈ 0.0179%
Q2: Is a low percentage always insignificant?
A2: No. The significance of a percentage depends heavily on the context. A low percentage of defects in a critical component of an aircraft is far more significant than a low percentage of defects in a less critical item.
Q3: What statistical tests can be used to analyze proportions like this?
A3: Chi-square tests and z-tests are commonly used for analyzing proportions and determining statistical significance.
Q4: How can I visualize this data effectively?
A4: Bar charts, pie charts, and tables are effective ways to visually represent this type of data.
Conclusion: Beyond the Numbers
The fraction 25 out of 140,000, while appearing small, holds significant implications depending on the context. Understanding proportions, percentages, and probability allows for a more nuanced interpretation of this ratio. Statistical analysis further aids in determining the significance of this number in various applications. By carefully considering the context and employing appropriate analytical techniques, we can glean valuable insights from seemingly small numerical representations. The ability to understand and interpret data like this is crucial across numerous fields and underscores the importance of mathematical and statistical literacy in our increasingly data-driven world. Remember that context is key, and a seemingly insignificant number can hold profound meaning when examined within the appropriate framework.
Latest Posts
Latest Posts
-
1 75 X 4
Sep 20, 2025
-
Half Of 49
Sep 20, 2025
-
150lbs En Kg
Sep 20, 2025
-
Cecil J Sharp
Sep 20, 2025
-
30 Of 360
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 140000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.