85 Of 480
interactiveleap
Sep 16, 2025 · 5 min read
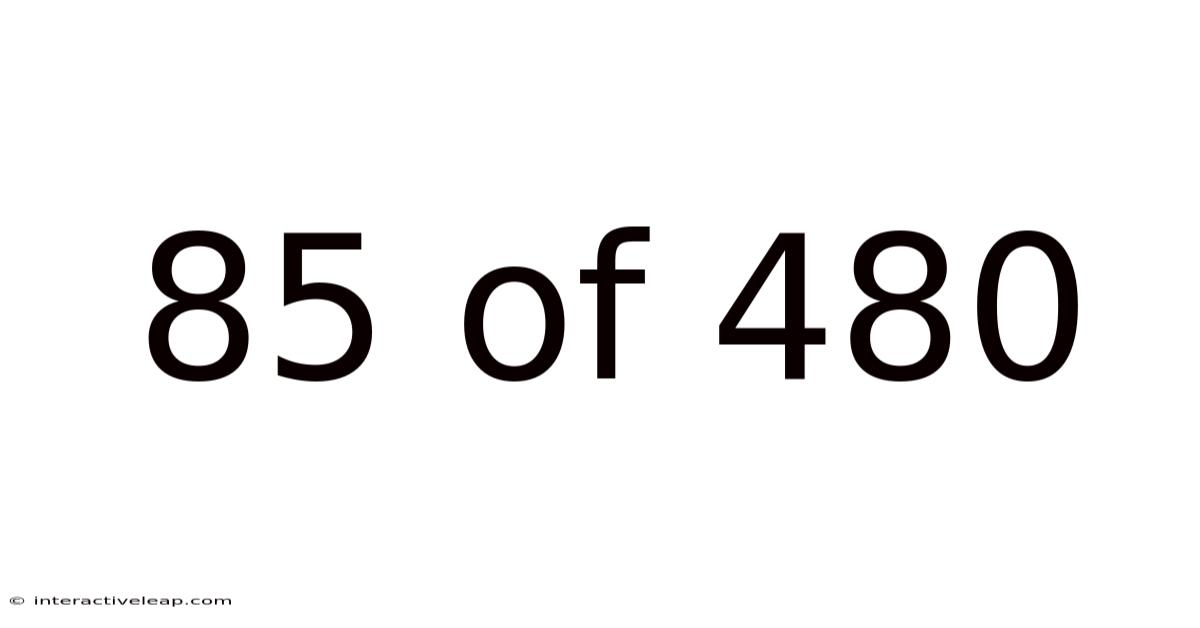
Table of Contents
Decoding Fractions: Understanding 85 out of 480
Understanding fractions is a fundamental skill in mathematics, applicable across various fields, from everyday calculations to complex scientific analyses. This article delves into the specific fraction 85/480, explaining how to simplify it, its decimal and percentage equivalents, and exploring its practical applications. We'll also examine related concepts to provide a comprehensive understanding of fraction manipulation. This guide will equip you with the tools to confidently tackle similar fraction problems.
Introduction: What Does 85/480 Represent?
The fraction 85/480 represents a part of a whole. Imagine you have 480 apples, and you take 85 of them. The fraction 85/480 shows the proportion of apples you've taken relative to the total number of apples. Understanding this fundamental representation is key to grasping fraction manipulation. This article aims to break down the processes involved in simplifying and interpreting this specific fraction, and also to provide a deeper understanding of fractions in general. We'll cover simplification, conversion to decimals and percentages, and discuss practical examples.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before delving into other representations, simplifying the fraction 85/480 makes it easier to work with. This involves finding the greatest common divisor (GCD) of both the numerator (85) and the denominator (480). The GCD is the largest number that divides both numbers without leaving a remainder.
There are several methods to find the GCD. One common method is the Euclidean algorithm:
-
Divide the larger number (480) by the smaller number (85): 480 ÷ 85 = 5 with a remainder of 55.
-
Replace the larger number with the remainder (55) and repeat the process: 85 ÷ 55 = 1 with a remainder of 30.
-
Continue this process until the remainder is 0:
- 55 ÷ 30 = 1 with a remainder of 25
- 30 ÷ 25 = 1 with a remainder of 5
- 25 ÷ 5 = 5 with a remainder of 0
The last non-zero remainder (5) is the GCD of 85 and 480.
Now, divide both the numerator and the denominator by the GCD (5):
- 85 ÷ 5 = 17
- 480 ÷ 5 = 96
Therefore, the simplified fraction is 17/96. This simplified form is much easier to work with than the original fraction.
Converting to Decimal: Understanding Decimal Equivalents
Converting a fraction to a decimal involves dividing the numerator by the denominator. For our simplified fraction, 17/96:
17 ÷ 96 ≈ 0.17708333...
This decimal representation shows the approximate value of the fraction. The decimal continues infinitely, as indicated by the ellipsis (...). For practical purposes, you might round the decimal to a specific number of decimal places depending on the context. For example, rounding to three decimal places gives us 0.177.
Converting to Percentage: Expressing as a Proportion of 100
Percentages are another way to represent fractions, expressing the value as a proportion of 100. To convert a decimal to a percentage, multiply the decimal by 100 and add a "%" sign.
Taking our decimal equivalent of 0.177:
0.177 x 100 = 17.7%
Therefore, 85/480 is approximately 17.7%. This percentage shows that 85 out of 480 represents about 17.7% of the whole.
Practical Applications: Real-World Examples
The fraction 85/480, or its simplified form 17/96, can be applied in various real-world scenarios. Here are some examples:
-
Test Scores: Imagine a test with 480 total points. A score of 85 points would represent 17/96 or approximately 17.7% of the total points.
-
Surveys and Statistics: In a survey of 480 people, 85 responded positively to a particular question. This represents 17/96 or approximately 17.7% of the respondents.
-
Inventory Management: If a warehouse contains 480 items and 85 are defective, the fraction 17/96 (or 17.7%) represents the proportion of defective items.
-
Financial Calculations: This fraction could represent a portion of a budget, investment return, or debt repayment.
These examples demonstrate the versatility of fractions in representing proportions and ratios in various contexts.
Further Exploration: Advanced Fraction Concepts
Understanding 85/480 provides a foundation for exploring more advanced fraction concepts:
-
Improper Fractions and Mixed Numbers: An improper fraction has a numerator larger than or equal to the denominator. A mixed number combines a whole number and a proper fraction. While 85/480 is a proper fraction, understanding the conversion between these forms is crucial for more complex calculations.
-
Fraction Addition and Subtraction: To add or subtract fractions, they must have a common denominator. This involves finding the least common multiple (LCM) of the denominators and adjusting the numerators accordingly.
-
Fraction Multiplication and Division: Multiplying fractions involves multiplying the numerators and denominators separately. Dividing fractions involves inverting the second fraction and then multiplying.
-
Complex Fractions: These fractions have fractions within the numerator or denominator, requiring multiple steps to simplify.
Mastering these concepts will greatly enhance your ability to work with fractions in more challenging mathematical problems.
Frequently Asked Questions (FAQ)
-
Q: What is the simplest form of 85/480?
- A: The simplest form of 85/480 is 17/96.
-
Q: How do I convert 85/480 to a decimal?
- A: Divide the numerator (85) by the denominator (480). The result is approximately 0.177.
-
Q: What is the percentage equivalent of 85/480?
- A: Approximately 17.7%.
-
Q: Why is simplifying fractions important?
- A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It provides a clearer representation of the proportion.
-
Q: What are some other methods to find the GCD?
- A: Besides the Euclidean algorithm, you can use prime factorization to find the GCD. This involves breaking down both numbers into their prime factors and finding the common factors.
Conclusion: Mastering Fractions for Success
Understanding fractions is a cornerstone of mathematical literacy. This article provided a detailed exploration of the fraction 85/480, covering simplification, decimal and percentage conversions, and practical applications. By grasping the concepts explained here and practicing with similar problems, you will build a strong foundation in fraction manipulation, enabling you to confidently tackle more complex mathematical challenges in various academic and real-world contexts. Remember that consistent practice is key to mastering fractions and building a strong understanding of mathematical principles. Don't be afraid to explore further and delve into the advanced concepts mentioned above to solidify your understanding.
Latest Posts
Latest Posts
-
3100g In Lbs
Sep 16, 2025
-
0 01 As Fraction
Sep 16, 2025
-
240kg To Lbs
Sep 16, 2025
-
6 5 X
Sep 16, 2025
-
13 Times 13
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 85 Of 480 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.