6 5 X
interactiveleap
Sep 16, 2025 · 7 min read
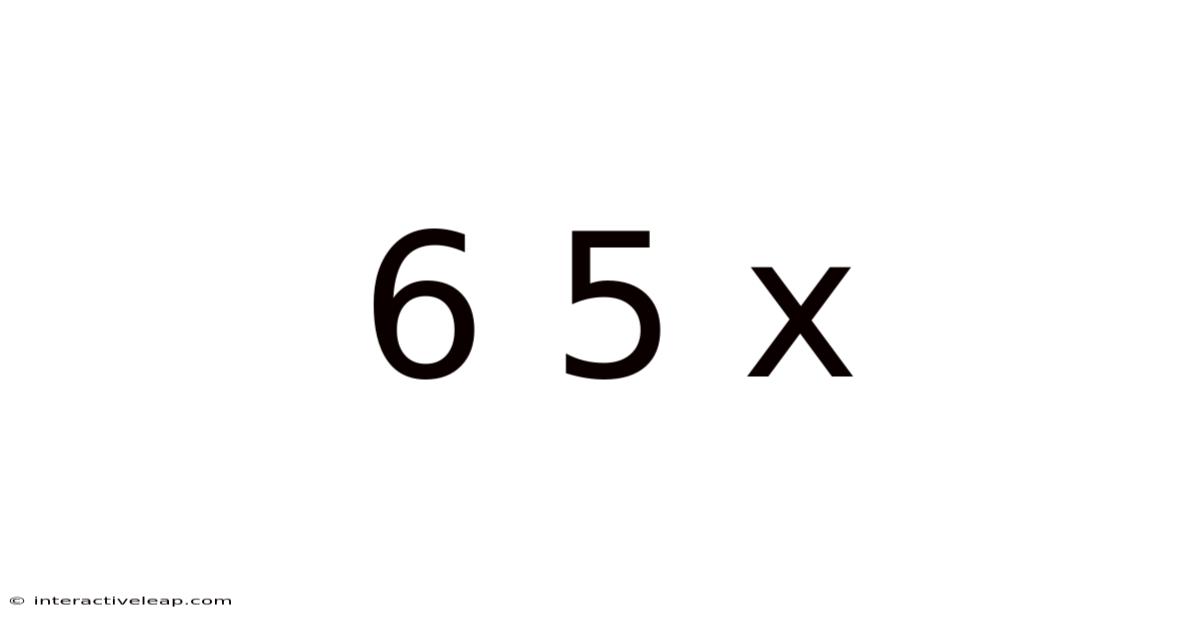
Table of Contents
Decoding 6 5 x: Exploring the World of Hexadecimal, Decimal, and Binary Number Systems
Understanding different number systems is fundamental to computer science, programming, and digital electronics. While we commonly use the decimal system (base-10), computers operate primarily using binary (base-2) and often utilize hexadecimal (base-16) for easier human interpretation of binary data. This article delves deep into the meaning and implications of "6 5 x," highlighting the relationships between these three crucial number systems, and providing a comprehensive understanding for beginners and experienced learners alike. This exploration will clarify the contexts in which such notation is used and why it's vital for various technological applications.
Introduction: The Foundation of Number Systems
Number systems are essentially ways of representing numerical quantities. Each system is defined by its base (or radix), which determines the number of unique digits used to represent numbers. The decimal system, familiar to everyone, has a base of 10, using digits 0 through 9. Binary, the language of computers, has a base of 2, using only 0 and 1. Hexadecimal, often used as a shorthand for binary, has a base of 16, utilizing digits 0-9 and letters A-F (A representing 10, B representing 11, and so on).
The notation "6 5 x" itself doesn't directly represent a single number in a specific system. Instead, it hints at the representation of a number across different bases. The 'x' acts as a placeholder, indicating that the same underlying quantity might be expressed differently in each system (decimal, hexadecimal, and binary). Let's examine how this works.
Understanding Decimal (Base-10)
The decimal system is the most intuitive for us because we learn it from a young age. Each digit in a decimal number represents a power of 10. For example, the number 1234 can be broken down as:
- 1 × 10³ (1000)
- 2 × 10² (100)
- 3 × 10¹ (10)
- 4 × 10⁰ (1)
Adding these together (1000 + 100 + 10 + 4) gives us 1234. This positional notation is crucial – the position of each digit determines its value.
Delving into Binary (Base-2)
Binary uses only two digits, 0 and 1. Each position represents a power of 2. Let's take the decimal number 13 as an example and convert it to binary:
- Find the largest power of 2 less than or equal to 13: 2³ = 8
- Subtract 8 from 13, leaving 5.
- Find the largest power of 2 less than or equal to 5: 2² = 4
- Subtract 4 from 5, leaving 1.
- Find the largest power of 2 less than or equal to 1: 2⁰ = 1
- Subtract 1 from 1, leaving 0.
Therefore, 13 in decimal is 1101 in binary (8 + 4 + 0 + 1 = 13). This binary representation is crucial because it's the fundamental language computers use to process information. Every piece of data, from text to images to videos, is ultimately represented as a sequence of 0s and 1s.
Exploring Hexadecimal (Base-16)
Hexadecimal is a base-16 system, using digits 0-9 and letters A-F (A=10, B=11, C=12, D=13, E=14, F=15). Its primary use is as a more compact representation of binary data. Because 16 is a power of 2 (16 = 2⁴), each hexadecimal digit corresponds to four binary digits (bits). This makes conversion between hexadecimal and binary incredibly straightforward.
For instance, let's convert the decimal number 255 to hexadecimal:
- Divide 255 by 16: 255 ÷ 16 = 15 with a remainder of 15.
- The remainder 15 is represented as F in hexadecimal.
- The quotient 15 is also represented as F in hexadecimal.
Therefore, 255 in decimal is FF in hexadecimal. This concise representation is highly beneficial when dealing with large binary numbers commonly encountered in computer memory addresses, color codes, and other data structures.
Conversions: Bridging the Gap Between Systems
Converting between decimal, binary, and hexadecimal is essential for understanding how computers work and manipulating digital data effectively. Several methods exist for these conversions, including:
- Decimal to Binary: Repeated division by 2, reading the remainders in reverse order.
- Binary to Decimal: Summing the powers of 2 corresponding to the positions of the 1s in the binary number.
- Decimal to Hexadecimal: Repeated division by 16, reading the remainders in reverse order.
- Hexadecimal to Decimal: Multiplying each hexadecimal digit by the corresponding power of 16 and summing the results.
- Binary to Hexadecimal: Grouping binary digits into sets of four (starting from the right) and converting each group into its hexadecimal equivalent.
- Hexadecimal to Binary: Converting each hexadecimal digit into its four-bit binary equivalent.
The Significance of "6 5 x" in Context
Returning to "6 5 x," we can now understand its meaning more clearly. It suggests a number expressed in three different bases:
- 6 (Decimal): The number six in the familiar base-10 system.
- 5 (Hexadecimal): The number five in base-16, representing the decimal value 5.
- x (Binary): A placeholder for the binary equivalent of the number represented by '6' and '5' in their respective systems. In this case, 'x' would be equivalent to the binary representation of the decimal number 6 and the decimal number 5, which would require a further specification to complete the meaning of this sequence. The "x" must represent the same numerical value if it’s part of a consistent set, implying it represents the binary form of either 6 or 5.
This notation highlights the interchangeability of these number systems. The underlying quantity remains the same; only the representation changes based on the chosen base. This understanding is paramount in working with computer hardware and software, where data is constantly being translated between these systems.
Advanced Concepts and Applications
The concepts discussed above form the foundation for various advanced topics in computer science and related fields:
- Bit manipulation: Directly manipulating individual bits within a binary number is crucial for tasks like setting flags, masking values, and optimizing performance.
- Data structures: Understanding binary and hexadecimal is essential for working with various data structures, such as arrays, linked lists, and trees, which often utilize binary or hexadecimal representation for addressing and data storage.
- Network protocols: Many network protocols, such as IP addressing, utilize binary and hexadecimal representations for efficient data transmission and routing.
- Hardware design: Digital logic circuits operate directly on binary data, so understanding binary and hexadecimal is essential for designing and troubleshooting hardware systems.
- Cryptography: Many cryptographic algorithms rely on binary and hexadecimal representations for encryption and decryption processes.
Frequently Asked Questions (FAQ)
Q: Why do we need different number systems?
A: We use different number systems for different purposes. Decimal is intuitive for humans, but binary is fundamental for computers. Hexadecimal provides a compact and human-readable way to represent binary data.
Q: How do I convert between these number systems quickly?
A: Practice is key! Using online converters initially is helpful, but mastering the conversion methods (repeated division/multiplication and positional notation) will significantly improve speed and understanding.
Q: Are there number systems beyond decimal, binary, and hexadecimal?
A: Absolutely! Octal (base-8), ternary (base-3), and other bases exist, each with its own specific applications, though they are less commonly used than the three discussed.
Q: What is the practical application of understanding these number systems?
A: Understanding these systems is crucial for anyone working with computers, programming, digital electronics, and data processing. It allows you to understand how data is represented, manipulated, and stored within a computer system.
Conclusion: Mastering the Fundamentals
This exploration of "6 5 x" has served as a gateway to understanding the interconnectedness of decimal, binary, and hexadecimal number systems. These systems are not isolated concepts; they are essential tools for comprehending the digital world. Mastering the principles of conversion and understanding the rationale behind each system's use will provide a significant advantage for anyone venturing into the fields of computer science, programming, or any area involving digital technologies. From software development to hardware design, a solid grasp of these foundational concepts is the key to unlocking a deeper understanding of how the digital world operates. The seemingly simple notation "6 5 x" therefore unlocks a wealth of knowledge crucial to navigating the complexities of modern technology.
Latest Posts
Latest Posts
-
20 Off 325
Sep 16, 2025
-
59 2kg In Stone
Sep 16, 2025
-
7 Of 300
Sep 16, 2025
-
30kg In Stones
Sep 16, 2025
-
40 Of 36
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 6 5 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.