85 Of 160
interactiveleap
Sep 20, 2025 · 6 min read
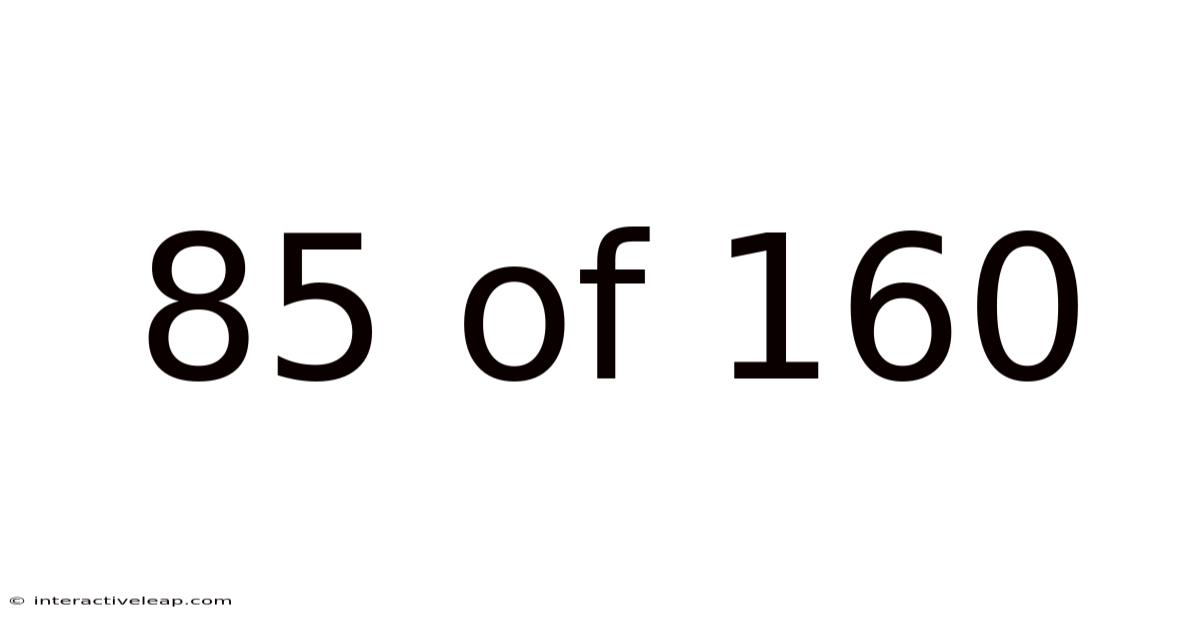
Table of Contents
Decoding 85/160: Understanding Fractions, Ratios, and Percentages
Understanding fractions, ratios, and percentages is fundamental to numerous aspects of life, from cooking and budgeting to advanced scientific calculations. This article delves deep into the meaning and implications of the fraction 85/160, exploring its simplification, conversion to a percentage and decimal, and its practical applications. We will also address common misconceptions and provide you with tools to confidently tackle similar problems.
Introduction: What Does 85/160 Represent?
The fraction 85/160 represents a part-to-whole relationship. It signifies that 85 is a portion of a larger whole, 160. This could represent anything from 85 correct answers out of 160 questions on a test to 85 sunny days out of 160 days in a particular season. Understanding this relationship is crucial for interpreting data and making informed decisions. This article will guide you through simplifying this fraction, converting it to a percentage and decimal, and understanding its implications within various contexts. Keywords: fraction, ratio, percentage, simplification, 85/160, mathematics.
1. Simplifying the Fraction 85/160
Before we delve into percentages and decimals, let's simplify the fraction 85/160. Simplifying a fraction means reducing it to its lowest terms, finding the greatest common divisor (GCD) of both the numerator (85) and the denominator (160).
The prime factorization method is a reliable way to find the GCD. Let's break down 85 and 160 into their prime factors:
- 85 = 5 x 17
- 160 = 2 x 2 x 2 x 2 x 2 x 5 = 2<sup>5</sup> x 5
The only common factor between 85 and 160 is 5. Therefore, we divide both the numerator and the denominator by 5:
85 ÷ 5 = 17 160 ÷ 5 = 32
Thus, the simplified fraction is 17/32. This simplified form represents the same proportion as 85/160 but is easier to work with.
2. Converting the Fraction to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. Using the simplified fraction 17/32:
17 ÷ 32 ≈ 0.53125
Therefore, the decimal equivalent of 85/160 is approximately 0.53125. The "approximately" is used because some fractions, when converted to decimals, result in non-terminating decimals (decimals that go on forever). In this case, the decimal terminates neatly.
3. Converting the Fraction to a Percentage
To convert a fraction to a percentage, we first convert it to a decimal (as we did above) and then multiply by 100. Using the decimal equivalent of 0.53125:
0.53125 x 100 = 53.125%
Therefore, 85/160 is equivalent to 53.125%. This means that 85 represents 53.125% of 160.
4. Practical Applications of 85/160 (and its equivalents)
The fraction 85/160, and its simplified and converted forms, find applications in diverse fields:
-
Academic Performance: Imagine a student scores 85 out of 160 on a test. Their score is 53.125%, which could then be compared to the average score of the class or other benchmark scores. This allows for evaluating the student's performance relative to others and understanding their areas for improvement.
-
Business and Finance: In sales, 85/160 could represent the proportion of sales targets achieved. A company aiming for 160 sales and achieving 85 would have achieved 53.125% of their goal. This information is crucial for evaluating sales performance and adjusting sales strategies.
-
Science and Engineering: In experiments, this fraction could represent the success rate of a particular process or the proportion of a substance used in a mixture. For example, in a clinical trial, 85 successful treatments out of 160 attempts would provide valuable information about the efficacy of a new treatment.
-
Everyday Life: This fraction could be used to calculate discounts, proportions in recipes, or to represent a portion of a larger task completed. For instance, if a project consists of 160 tasks and 85 are completed, then 53.125% of the project is finished.
5. Understanding Ratios
The fraction 85/160 can also be expressed as a ratio: 85:160 or, in its simplified form, 17:32. A ratio shows the relative size of two or more values. In this case, it indicates the relationship between the part (85) and the whole (160). Ratios are particularly useful when comparing quantities. For example, if two different groups of students took the same test, the ratio could be used to compare their relative performances.
6. Common Misconceptions
Several misconceptions surround fractions, percentages, and ratios:
-
Confusion between fractions and decimals: Some students struggle to correctly convert between fractions and decimals. Understanding the core concept – that a fraction represents division – is crucial for accurate conversion.
-
Difficulty simplifying fractions: Finding the greatest common divisor can be challenging. Mastering prime factorization techniques is essential for efficient simplification.
-
Incorrect percentage calculations: Errors often arise when multiplying by 100 to convert a decimal to a percentage or when making the inverse calculation. Careful attention to detail is paramount.
-
Misinterpretation of ratios: Understanding the order of values in a ratio and its meaning within context is crucial.
7. Frequently Asked Questions (FAQ)
-
Q: Is 85/160 an improper or proper fraction? A: 85/160 is a proper fraction because the numerator (85) is less than the denominator (160).
-
Q: What is the reciprocal of 85/160? A: The reciprocal of 85/160 is 160/85, which simplifies to 32/17.
-
Q: How can I check if my simplification is correct? A: To verify simplification, divide the original numerator and denominator by the GCD. The resulting fraction should be the simplified version. You can also check that the decimal and percentage values remain consistent across the simplified and original fractions.
-
Q: Why is simplifying fractions important? A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It presents the data in its most concise form.
-
Q: Are there any online tools that can help with fraction simplification? A: Yes, many online calculators and websites offer fraction simplification tools. These tools can be helpful for checking your work or handling more complex fractions.
8. Conclusion: Mastering Fractions, Ratios, and Percentages
Mastering fractions, ratios, and percentages is a fundamental skill with far-reaching applications. The seemingly simple fraction 85/160, once simplified and converted, unlocks a deeper understanding of proportions and relative quantities. By understanding the underlying concepts and practicing conversion techniques, you can confidently tackle similar problems in various academic, professional, and everyday situations. The process of simplifying 85/160 into 17/32, converting it to its decimal equivalent (0.53125), and its percentage (53.125%) illustrates the interconnectedness of these mathematical concepts. This knowledge empowers you to interpret data, solve problems, and make informed decisions across numerous contexts. Remember that consistent practice and a strong understanding of the fundamentals are key to mastering these crucial mathematical skills.
Latest Posts
Latest Posts
-
4 X 34
Sep 20, 2025
-
33 Of 34567
Sep 20, 2025
-
1 8 In Fraction
Sep 20, 2025
-
3 Of 70000
Sep 20, 2025
-
25 Of 340
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 85 Of 160 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.