25 Of 340
interactiveleap
Sep 20, 2025 · 6 min read
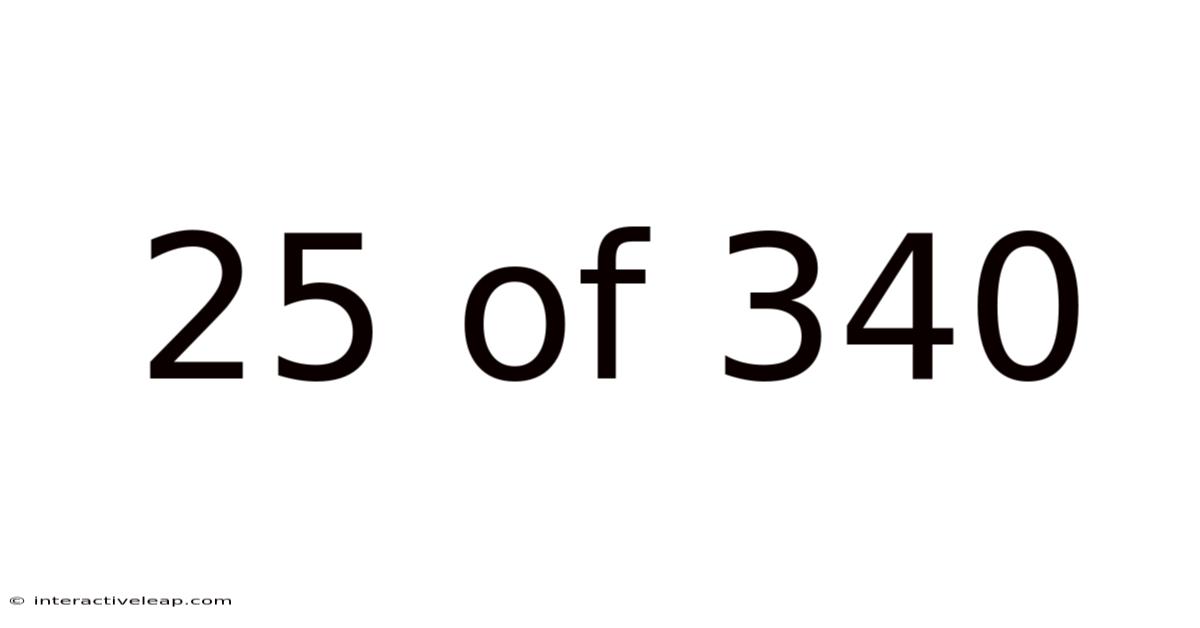
Table of Contents
Understanding the Fraction 25/340: Simplification, Applications, and Beyond
The seemingly simple fraction 25/340 might appear insignificant at first glance. However, understanding its simplification, practical applications, and the broader mathematical concepts it represents opens a door to a deeper appreciation of numerical relationships. This article will explore 25/340 in detail, covering its reduction to its simplest form, various contexts in which it could arise, and related mathematical ideas. We'll delve into the process, explaining the steps clearly and concisely, making it accessible to learners of all levels.
Introduction: A Deep Dive into 25/340
The fraction 25/340 represents a part-to-whole relationship. It signifies 25 units out of a total of 340 units. While seemingly straightforward, understanding how to simplify this fraction and its implications is crucial for developing a strong foundation in mathematics. This article aims to provide a comprehensive understanding of 25/340, from basic simplification to its potential applications in various real-world scenarios. We will also touch upon the broader mathematical principles involved, making this exploration both informative and insightful.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
The first step in working with any fraction is to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of the numerator (25) and the denominator (340). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
We can find the GCD using several methods:
-
Listing Factors: List all the factors of 25 and 340. The factors of 25 are 1, 5, and 25. The factors of 340 are 1, 2, 4, 5, 10, 17, 20, 34, 68, 85, 170, and 340. The greatest common factor is 5.
-
Prime Factorization: Express both numbers as a product of their prime factors.
- 25 = 5 x 5 = 5²
- 340 = 2 x 2 x 5 x 17 = 2² x 5 x 17
The common prime factor is 5. Therefore, the GCD is 5.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. We repeatedly apply the division algorithm until we reach a remainder of 0. The last non-zero remainder is the GCD.
- 340 ÷ 25 = 13 with a remainder of 15
- 25 ÷ 15 = 1 with a remainder of 10
- 15 ÷ 10 = 1 with a remainder of 5
- 10 ÷ 5 = 2 with a remainder of 0
The last non-zero remainder is 5, so the GCD is 5.
2. Simplifying 25/340 to its Lowest Terms
Now that we've found the GCD to be 5, we can simplify the fraction:
25/340 = (25 ÷ 5) / (340 ÷ 5) = 5/68
Therefore, the simplified form of 25/340 is 5/68. This represents the same proportion but in a more concise and manageable form.
3. Real-World Applications of the Fraction 25/340 (and its simplified form 5/68)
While the fraction 25/340 might not immediately jump out as having obvious real-world applications, understanding its simplification helps us understand proportional relationships that appear in various situations:
-
Percentage Calculations: The fraction 5/68 can be converted to a percentage by multiplying by 100: (5/68) * 100 ≈ 7.35%. This could represent a discount, a success rate, or a proportion in many contexts. Imagine a test with 68 questions; answering 5 correctly would mean achieving approximately a 7.35% score.
-
Ratio Problems: The ratio 5:68 could represent a mixture, a comparison of quantities, or any situation involving proportions. For example, if a recipe calls for a 5:68 ratio of ingredient A to ingredient B, you would use 5 units of A for every 68 units of B.
-
Probability: If there are 68 equally likely outcomes in an experiment, and 5 of them represent a specific event, the probability of that event occurring is 5/68, or approximately 7.35%.
-
Data Analysis: In statistical analysis, you might encounter proportions similar to 5/68 when calculating relative frequencies or probabilities.
-
Geometry and Measurement: Imagine a situation where you're dealing with areas or lengths of objects. The ratio 5/68 could represent the relationship between the size of two shapes or the length of two segments.
4. Mathematical Concepts Related to 25/340
The fraction 25/340, and its simplified form 5/68, provides opportunities to explore several key mathematical concepts:
-
Rational Numbers: Fractions are rational numbers – numbers that can be expressed as the ratio of two integers (where the denominator is not zero). 25/340 is a rational number.
-
Equivalent Fractions: 25/340 and 5/68 are equivalent fractions; they represent the same value. This highlights the concept of equivalence and simplification within the number system.
-
Decimal Representation: The fraction 5/68 can be converted to a decimal by performing the division: 5 ÷ 68 ≈ 0.0735. Understanding the relationship between fractions and decimals is important in various mathematical applications.
-
Percentage Conversion: As mentioned earlier, converting a fraction to a percentage provides a readily understandable representation of the proportion.
-
Ratio and Proportion: The simplified fraction 5/68 embodies the concept of ratio and proportion, which are fundamental to various aspects of mathematics and its applications.
5. Frequently Asked Questions (FAQs)
-
Q: Why is it important to simplify fractions?
- A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also allows for clearer visualization of the relationship between the numerator and the denominator.
-
Q: Are there other ways to simplify 25/340 besides using the GCD?
- A: While finding the GCD is the most efficient method, you could also simplify the fraction step-by-step by dividing both the numerator and the denominator by common factors until you reach the lowest terms. For instance, you could first divide by 5, then see if any further common factors exist.
-
Q: Can any fraction be simplified?
- A: Not all fractions can be simplified. If the numerator and denominator share no common factors other than 1 (i.e., their GCD is 1), the fraction is already in its simplest form. Such fractions are called irreducible fractions.
-
Q: What happens if the denominator of a fraction is zero?
- A: Division by zero is undefined in mathematics. A fraction with a denominator of zero is not a valid mathematical expression.
-
Q: How can I practice simplifying fractions?
- A: Practice makes perfect! Start with simple fractions and gradually work towards more complex ones. Use online resources, textbooks, and worksheets to find exercises and test your understanding.
6. Conclusion: Beyond the Fraction
The exploration of the fraction 25/340 has taken us beyond a simple numerical expression. We've delved into the process of simplification, uncovered practical applications, and touched upon fundamental mathematical concepts. Understanding fractions like 25/340 builds a solid foundation for more advanced mathematical studies, such as algebra, calculus, and statistics. The seemingly insignificant 25/340, reduced to its simplest form 5/68, reveals the elegance and interconnectedness of mathematical ideas. By mastering the techniques presented here, you can confidently tackle similar fraction problems and apply the underlying principles to various real-world situations. Remember, the journey of mathematical understanding is a continuous process of exploration and discovery.
Latest Posts
Latest Posts
-
15 Off 120
Sep 20, 2025
-
Map With Colours
Sep 20, 2025
-
25mph To Kmh
Sep 20, 2025
-
Mj In J
Sep 20, 2025
-
10000km In Miles
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 340 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.