80 Of 34
interactiveleap
Sep 19, 2025 · 5 min read
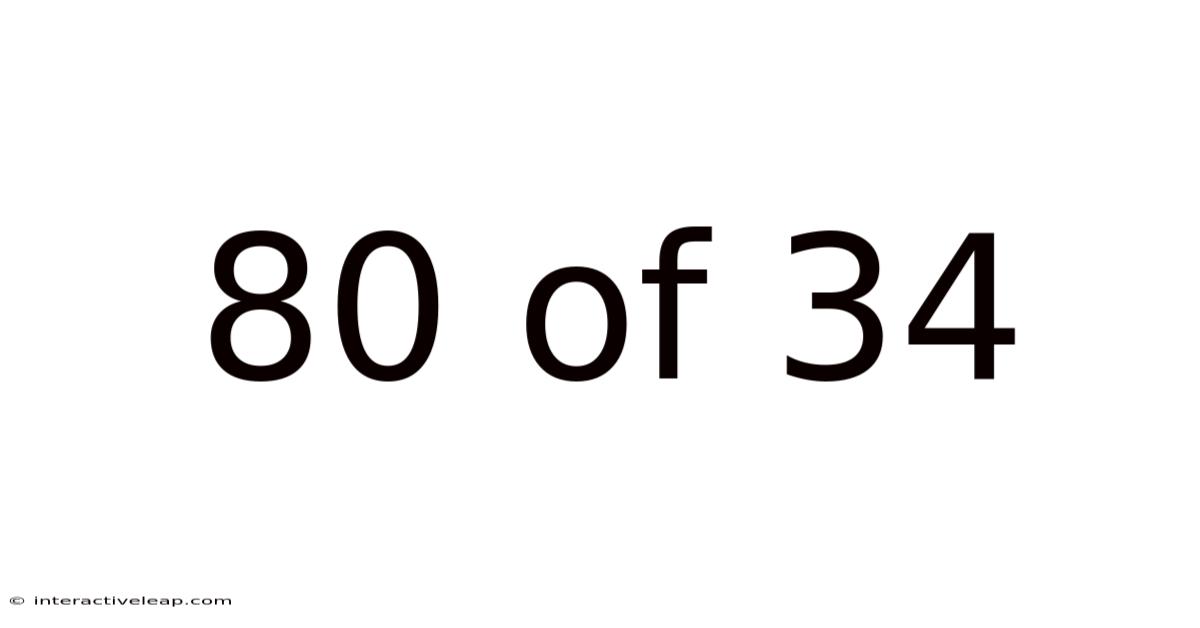
Table of Contents
Decoding the Fraction: Understanding 80/34 and its Implications
What does 80/34 mean? At first glance, this fraction might seem simple, but it opens a door to a world of mathematical concepts – from basic arithmetic to more advanced topics like ratios, percentages, and even algebraic manipulation. This article will delve deep into the meaning and applications of 80/34, exploring its simplification, decimal representation, percentage equivalent, and practical applications in various contexts. We will also touch upon related concepts to provide a comprehensive understanding of this seemingly simple fraction.
Understanding Fractions: A Quick Refresher
Before we dive into 80/34, let's quickly recap the basics of fractions. A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1 and the denominator is 2, representing one out of two equal parts.
Simplifying the Fraction 80/34
The fraction 80/34 isn't in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of both the numerator and the denominator. The GCD is the largest number that divides both numbers without leaving a remainder. Let's find the GCD of 80 and 34.
One way to find the GCD is through prime factorization. The prime factorization of 80 is 2<sup>4</sup> x 5, and the prime factorization of 34 is 2 x 17. The only common factor is 2. Therefore, the GCD of 80 and 34 is 2.
Now, we divide both the numerator and the denominator by the GCD:
80 ÷ 2 = 40 34 ÷ 2 = 17
Therefore, the simplified form of 80/34 is 40/17. This simplified fraction is equivalent to the original fraction, but it's easier to work with.
Converting to Decimal: Understanding the Decimal Representation
Converting a fraction to a decimal involves dividing the numerator by the denominator. Let's divide 40 by 17:
40 ÷ 17 ≈ 2.3529
Therefore, the decimal representation of 80/34 (or 40/17) is approximately 2.3529. The result is a decimal that doesn't terminate (it goes on forever), meaning it's a repeating decimal or irrational number in this case. We often round it to a certain number of decimal places depending on the required level of precision.
Expressing as a Percentage: The Percentage Equivalent
To convert a fraction to a percentage, we first convert the fraction to a decimal and then multiply by 100%.
Using our decimal approximation of 2.3529:
2.3529 x 100% ≈ 235.29%
Therefore, 80/34 is approximately 235.29%. This means that 80 is approximately 235.29% of 34. This percentage is greater than 100% because the numerator is larger than the denominator.
Practical Applications of 80/34
The fraction 80/34, and its simplified form 40/17, can appear in various real-world scenarios. Here are a few examples:
-
Ratio and Proportion: Imagine you have a mixture containing 80 grams of ingredient A and 34 grams of ingredient B. The ratio of ingredient A to ingredient B is 80:34, which simplifies to 40:17. This ratio helps understand the proportion of each ingredient in the mixture.
-
Calculating Percentages: If you scored 80 out of 34 possible points on a test (perhaps a test with bonus points!), the fraction 80/34 represents your performance. As we've calculated, this translates to approximately 235.29%, highlighting a significant overachievement.
-
Scaling and Measurement: If a map's scale indicates that 34 centimeters on the map represents 80 kilometers in reality, the fraction 80/34 helps convert measurements between the map and the actual distances.
-
Algebra and Equations: The fraction can be part of algebraic expressions and equations. For example, solving the equation x/34 = 80/17 involves using proportional reasoning and finding the value of x.
Further Exploration: Related Mathematical Concepts
Understanding 80/34 opens doors to explore more complex mathematical concepts:
-
Improper Fractions and Mixed Numbers: 80/34 is an improper fraction because the numerator is larger than the denominator. It can be converted to a mixed number, which is a combination of a whole number and a proper fraction. Dividing 80 by 34, we get 2 with a remainder of 12. Therefore, 80/34 can be written as the mixed number 2 12/34. This simplifies further to 2 6/17.
-
Rational and Irrational Numbers: The fraction 80/34 represents a rational number because it can be expressed as a ratio of two integers. Its decimal representation, although non-terminating, is a repeating decimal, which also classifies it as a rational number.
-
Proportionality and Ratio Analysis: The fraction and its simplified form (40/17) are crucial in understanding proportions and ratios, fundamental concepts in various fields like science, engineering, and finance.
-
Algebraic Manipulation: The fraction 80/34 can be used in various algebraic manipulations, including solving equations, simplifying expressions, and working with proportional relationships.
Frequently Asked Questions (FAQ)
Q1: What is the simplest form of 80/34?
A1: The simplest form of 80/34 is 40/17.
Q2: What is the decimal equivalent of 80/34?
A2: The decimal equivalent of 80/34 is approximately 2.3529.
Q3: What is the percentage equivalent of 80/34?
A3: The percentage equivalent of 80/34 is approximately 235.29%.
Q4: Can 80/34 be expressed as a mixed number?
A4: Yes, 80/34 can be expressed as the mixed number 2 6/17.
Conclusion: A Deeper Understanding of 80/34
This in-depth exploration of the fraction 80/34 reveals that seemingly simple mathematical objects can lead to a richer understanding of various mathematical concepts. From simplification and conversion to practical applications and advanced concepts, the analysis of 80/34 demonstrates the interconnectedness of mathematical ideas and their relevance in diverse fields. Remember, a strong foundation in basic arithmetic, including fraction manipulation, is crucial for tackling more complex mathematical challenges. This analysis provides a clear pathway to understanding this specific fraction and broadens your understanding of related concepts, allowing you to confidently approach similar problems in the future.
Latest Posts
Latest Posts
-
1 3 Of 30
Sep 19, 2025
-
Define Brake Fade
Sep 19, 2025
-
7 Of 250
Sep 19, 2025
-
Roman Villa Layout
Sep 19, 2025
-
43kg To Stone
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 34 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.