1/3 Of 30
interactiveleap
Sep 19, 2025 · 7 min read
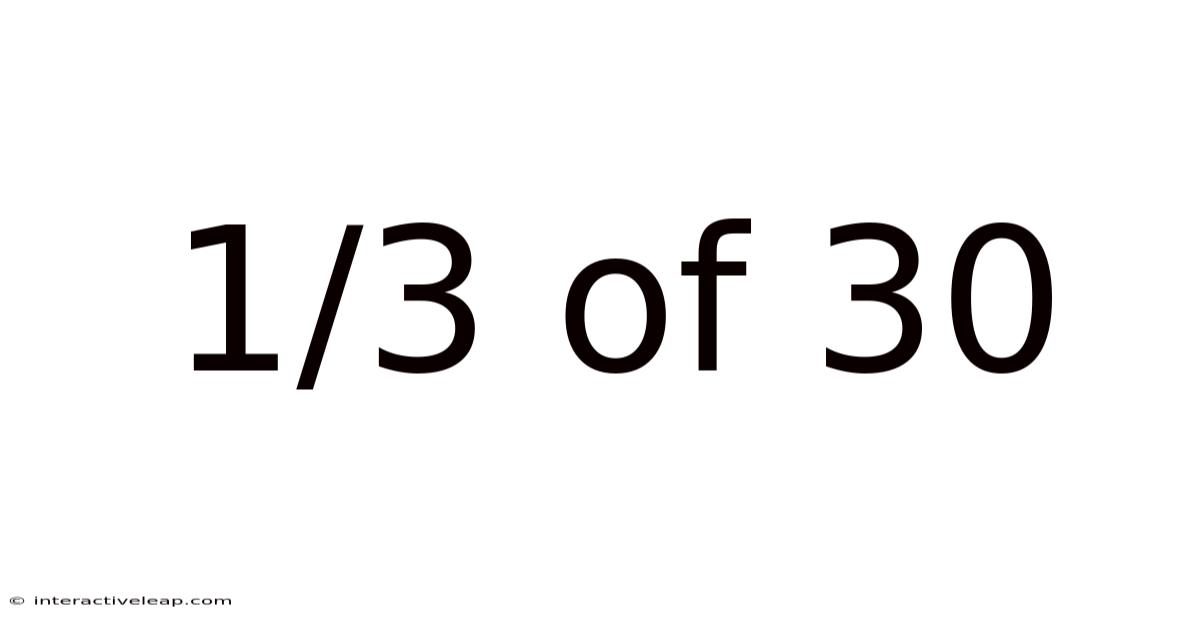
Table of Contents
Decoding 1/3 of 30: A Deep Dive into Fractions and Their Applications
This article explores the seemingly simple calculation of "1/3 of 30," delving beyond the immediate answer to uncover the underlying principles of fractions, their practical applications, and the broader mathematical concepts they represent. Understanding this seemingly basic problem unlocks a deeper understanding of fundamental arithmetic and lays the groundwork for more complex mathematical operations. We will explore various methods for solving this problem, discuss the importance of fractions in everyday life, and address frequently asked questions.
Understanding Fractions: The Building Blocks
Before tackling 1/3 of 30, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows how many equal parts the whole is divided into. In the fraction 1/3, 1 is the numerator and 3 is the denominator. This means we are considering one part out of three equal parts.
Calculating 1/3 of 30: Three Different Approaches
There are several ways to calculate 1/3 of 30. Each method offers a slightly different perspective on the same mathematical operation.
Method 1: Direct Multiplication
The most straightforward approach involves multiplying the fraction 1/3 by the whole number 30. This is done by multiplying the numerator (1) by 30 and then dividing the result by the denominator (3):
(1/3) * 30 = (1 * 30) / 3 = 30 / 3 = 10
Therefore, 1/3 of 30 is 10.
Method 2: Division First
Alternatively, we can first divide the whole number (30) by the denominator (3) and then multiply the result by the numerator (1):
30 / 3 = 10 10 * 1 = 10
This method highlights the concept of dividing the whole into equal parts before selecting the desired number of parts.
Method 3: Visual Representation
A visual approach can help solidify the understanding, especially for beginners. Imagine a circle or a rectangle divided into three equal parts. Each part represents 1/3 of the whole. If the whole represents 30, then each of the three equal parts would represent 30 / 3 = 10. Therefore, 1/3 of 30 is 10. This method is particularly useful for visualizing fractions and understanding their meaning intuitively.
Beyond the Calculation: The Significance of Fractions in Everyday Life
Fractions are not just abstract mathematical concepts; they are integral to our daily lives. Consider these examples:
- Cooking and Baking: Recipes often involve fractional measurements (e.g., 1/2 cup of sugar, 2/3 cup of flour). Understanding fractions is crucial for accurately measuring ingredients and achieving desired results.
- Shopping and Budgeting: Discounts and sales are frequently expressed as fractions (e.g., 1/3 off, 25% off, which is equivalent to 1/4 off). Knowing how to calculate fractions allows for smart shopping and budget management.
- Time Management: Dividing time into fractions helps with scheduling and task management (e.g., spending 1/4 of the day on work, 1/3 on family time).
- Measurement and Construction: Fractions are fundamental in construction, engineering, and other fields involving precise measurements. Understanding fractions ensures accurate measurements and construction.
- Data Analysis and Statistics: Fractions and percentages (which are essentially fractions expressed as a part of 100) are extensively used in data analysis and statistics to represent proportions and probabilities.
Exploring Related Concepts: Percentages, Decimals, and Ratios
Fractions are closely related to percentages and decimals. A percentage is a fraction expressed as a part of 100. For example, 1/3 can be expressed as a percentage by dividing 1 by 3 and multiplying the result by 100: (1/3) * 100 ≈ 33.33%. Similarly, a decimal is a fraction expressed as a base-10 number. 1/3 expressed as a decimal is approximately 0.333... (a recurring decimal).
Fractions are also fundamentally linked to ratios. A ratio compares the relative sizes of two or more quantities. For example, if there are 10 apples and 20 oranges, the ratio of apples to oranges is 10:20, which simplifies to 1:2. This shows that for every apple, there are two oranges. This concept is essential in various fields, including chemistry, physics, and cooking.
Extending the Concept: Calculating Fractions of Larger Numbers
The same principles used to calculate 1/3 of 30 apply to calculating fractions of larger numbers. For example, to calculate 1/3 of 90, we can use any of the previously described methods:
- Direct Multiplication: (1/3) * 90 = (1 * 90) / 3 = 90 / 3 = 30
- Division First: 90 / 3 = 30; 30 * 1 = 30
- Visual Representation: Imagine a shape divided into three equal parts. If the whole represents 90, each part would represent 90/3 = 30.
Similarly, we can calculate other fractions of 30 or other numbers using the same approach. For instance, to find 2/3 of 30:
- Direct Multiplication: (2/3) * 30 = (2 * 30) / 3 = 60 / 3 = 20
- Division First: 30 / 3 = 10; 10 * 2 = 20
This demonstrates that the core principle of multiplying the numerator by the whole number and then dividing by the denominator remains consistent regardless of the size of the number or the fraction involved.
Working with Improper Fractions and Mixed Numbers
So far, we've focused on proper fractions (where the numerator is smaller than the denominator). However, we can also work with improper fractions (where the numerator is greater than or equal to the denominator) and mixed numbers (a combination of a whole number and a proper fraction).
For example, let's find 5/3 of 30:
- Direct Multiplication: (5/3) * 30 = (5 * 30) / 3 = 150 / 3 = 50
This calculation shows that even with improper fractions, the same principles apply. The result (50) is greater than 30, which makes sense because we're taking more than the whole (5/3 is greater than 1).
A mixed number like 1 2/3 can be converted into an improper fraction before performing the calculation. 1 2/3 is equivalent to (3 + 2)/3 = 5/3. Therefore, 1 2/3 of 30 would also be 50.
Frequently Asked Questions (FAQ)
Q1: What if I need to calculate a fraction of a number that doesn't divide evenly?
A: In some cases, the result will be a fraction or a decimal. For example, 1/7 of 30 is approximately 4.286. Use a calculator or perform long division to get the exact or approximate result.
Q2: How do I simplify fractions?
A: Simplifying a fraction involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD. For example, 6/9 can be simplified to 2/3 by dividing both the numerator and the denominator by 3 (the GCD of 6 and 9).
Q3: What are some real-world applications of calculating fractions of numbers?
A: Real-world applications are vast and varied, ranging from calculating discounts and sales tax to determining proportions in recipes, calculating area and volume, and even modeling probabilities in various fields.
Q4: Is there a specific formula for calculating fractions of numbers?
A: Yes, the general formula is: (numerator / denominator) * whole number. This formula applies to all types of fractions, including proper, improper, and mixed numbers.
Conclusion: Mastering Fractions: A Gateway to Higher Mathematics
This comprehensive exploration of "1/3 of 30" has revealed the fundamental principles of fractions, their practical significance, and their connection to other mathematical concepts. While the initial problem appears simple, it serves as a gateway to a deeper understanding of arithmetic, laying a solid foundation for more advanced mathematical studies. Proficiency in handling fractions is crucial not only for academic success but also for navigating the quantitative aspects of everyday life. Remember, mastering fractions is not just about getting the right answer; it's about understanding the underlying principles and applying them creatively to solve real-world problems.
Latest Posts
Latest Posts
-
116lbs In Kg
Sep 19, 2025
-
Al Banna Hassan
Sep 19, 2025
-
80 Of 24
Sep 19, 2025
-
Binary For 17
Sep 19, 2025
-
40cm To Mm
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1/3 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.