80 Of 32
interactiveleap
Sep 19, 2025 · 6 min read
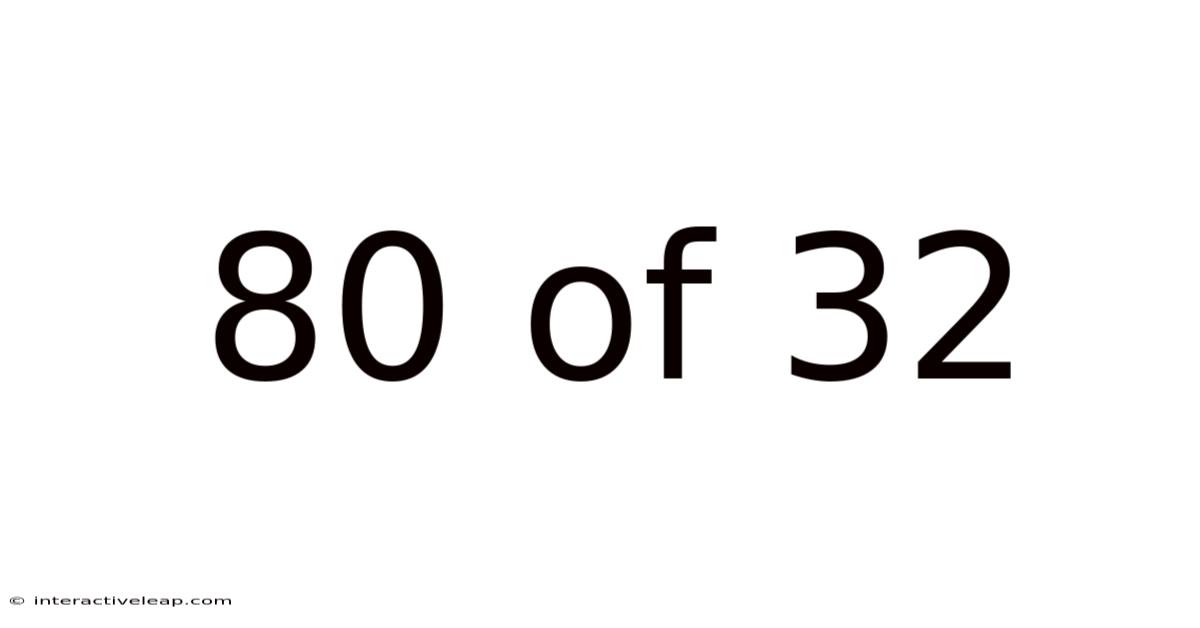
Table of Contents
Decoding 80/32: Understanding the Fraction and its Applications
This article delves into the seemingly simple fraction 80/32, exploring its various interpretations, simplifications, decimal equivalents, and applications across different fields. We'll move beyond basic arithmetic to uncover the deeper meaning and context of this fraction, revealing its usefulness in problem-solving and real-world scenarios. Understanding fractions like 80/32 is fundamental to grasping more complex mathematical concepts.
Introduction: What is 80/32?
At first glance, 80/32 appears to be a straightforward fraction. It represents the ratio of 80 parts to 32 parts of a whole. However, this seemingly simple fraction holds a wealth of mathematical properties and practical implications. This article aims to explore these aspects in detail, guiding you through simplification, decimal conversion, and real-world applications. We'll also examine how this fraction relates to percentages, proportions, and other fundamental mathematical concepts.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before proceeding further, it's crucial to simplify the fraction 80/32 to its lowest terms. This process involves finding the greatest common divisor (GCD) of both the numerator (80) and the denominator (32). The GCD is the largest number that divides both 80 and 32 without leaving a remainder.
One method to find the GCD is through prime factorization. Let's break down 80 and 32 into their prime factors:
- 80 = 2 x 2 x 2 x 2 x 5 = 2<sup>4</sup> x 5
- 32 = 2 x 2 x 2 x 2 x 2 = 2<sup>5</sup>
The common prime factors are 2<sup>4</sup>. Therefore, the GCD of 80 and 32 is 16.
To simplify the fraction, we divide both the numerator and the denominator by the GCD:
80/32 = (80 ÷ 16) / (32 ÷ 16) = 5/2
Therefore, the simplified form of the fraction 80/32 is 5/2. This simplified form is easier to work with and represents the same ratio.
Converting to Decimal: From Fraction to Decimal Representation
Converting the fraction 5/2 to its decimal equivalent is a straightforward process. We simply divide the numerator (5) by the denominator (2):
5 ÷ 2 = 2.5
Thus, the decimal representation of 80/32 (and its simplified form 5/2) is 2.5. This decimal form is often preferred for calculations and comparisons, especially in contexts where dealing with fractions might be cumbersome.
Understanding the Ratio: Interpreting 80/32 in Context
The ratio 80:32, or its simplified form 5:2, signifies that for every 5 units of one quantity, there are 2 units of another. This ratio can be applied in various scenarios:
- Proportions: If you have 80 apples and 32 oranges, the ratio of apples to oranges is 80:32, or simplified to 5:2. This means there are 5 apples for every 2 oranges.
- Scaling: Imagine enlarging a picture. If the original dimensions are 32 pixels wide and 80 pixels high, the aspect ratio is 80:32 or 5:2. Enlarging the picture while maintaining the aspect ratio means increasing the width and height proportionally. For example, doubling the width to 64 pixels would require doubling the height to 160 pixels.
- Rates: Consider a car traveling 80 kilometers in 32 minutes. The average speed is 80 km / 32 min, which simplifies to 2.5 km/min.
Applications in Different Fields:
The fraction 80/32, or its simplified equivalent 5/2, finds application in various fields:
- Engineering: In engineering design, ratios are crucial. For instance, the ratio of the height to the base of a structure might be expressed as a fraction.
- Finance: Financial ratios, like the debt-to-equity ratio, are expressed as fractions to assess a company's financial health.
- Cooking and Baking: Recipes often require specific ratios of ingredients. A recipe calling for 80 grams of flour and 32 grams of sugar has a flour-to-sugar ratio of 5:2.
- Science: In scientific experiments, ratios are fundamental for calculating concentrations, dilutions, and other quantitative measures.
- Computer Science: Aspect ratios of images or screen resolutions can be represented as fractions.
Percentage Representation: Expressing the Ratio as a Percentage
To express the fraction 80/32 (or 5/2) as a percentage, we first convert it to a decimal (2.5) and then multiply by 100:
2.5 x 100 = 250%
This means 80 is 250% of 32. It's important to note that percentages exceeding 100% indicate that the numerator is greater than the denominator.
Working with the Fraction in Equations:
Let's illustrate how to use the fraction 80/32 (or 5/2) in simple equations:
- Solving for x: If x/4 = 5/2, then cross-multiplying gives 2x = 20, so x = 10.
- Adding Fractions: Adding 80/32 to another fraction, say 1/2, requires finding a common denominator. Since 80/32 simplifies to 5/2, we have 5/2 + 1/2 = 6/2 = 3.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying a fraction important?
A1: Simplifying a fraction reduces it to its lowest terms, making it easier to understand, compare, and use in calculations. It also improves clarity and avoids unnecessary complexity.
Q2: Can I use a calculator to simplify fractions?
A2: Yes, many calculators have a function to simplify fractions automatically. However, understanding the underlying principles of finding the GCD is crucial for a deeper mathematical understanding.
Q3: What if I have a fraction where the denominator is zero?
A3: A fraction with a denominator of zero is undefined. Division by zero is not a valid mathematical operation.
Q4: How do I convert a decimal back into a fraction?
A4: To convert a decimal to a fraction, write the decimal as a fraction with a denominator of a power of 10 (e.g., 10, 100, 1000). Then simplify the fraction to its lowest terms. For example, 0.75 can be written as 75/100, which simplifies to 3/4.
Conclusion: The Significance of Understanding Fractions
The seemingly simple fraction 80/32, through its simplification to 5/2 and its various representations (decimal, percentage, ratio), showcases the versatility and practical importance of fractions in mathematics and its various applications. Mastering the concepts presented here – simplification, decimal conversion, ratio interpretation, and problem-solving involving fractions – forms a strong foundation for more advanced mathematical concepts and real-world applications across multiple disciplines. Understanding how to manipulate and interpret fractions like 80/32 is essential for anyone seeking a strong grasp of quantitative reasoning and problem-solving. This knowledge empowers you to confidently tackle more complex mathematical challenges and apply your skills effectively in various contexts. Remember, the key is to understand the underlying principles rather than simply memorizing procedures. By grasping the core concepts, you unlock a broader understanding of the world around you.
Latest Posts
Latest Posts
-
Artifacts And Culture
Sep 19, 2025
-
40 Of 320
Sep 19, 2025
-
Negative Reciprocal Of
Sep 19, 2025
-
15 Of 210
Sep 19, 2025
-
9 Times 11
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.