80 Of 280
interactiveleap
Sep 20, 2025 · 6 min read
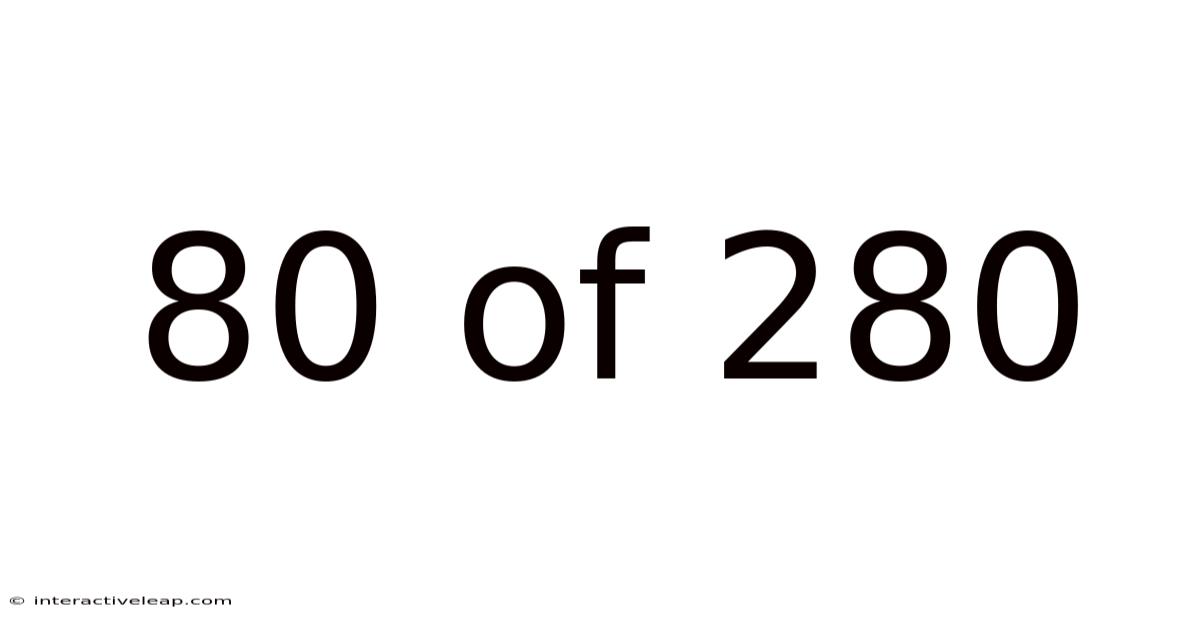
Table of Contents
Understanding the Fraction 80/280: Simplification, Decimals, and Applications
The fraction 80/280, while seemingly complex at first glance, represents a simple mathematical concept that can be understood and applied in various contexts. This article will guide you through the process of simplifying this fraction, converting it to a decimal, and exploring its practical applications. We'll also delve into the underlying principles of fraction reduction and decimal conversion, ensuring a comprehensive understanding of this particular fraction and the broader mathematical concepts it embodies.
Introduction: What Does 80/280 Mean?
The fraction 80/280 represents 80 parts out of a total of 280 parts. Think of it like having 80 slices of pizza out of a total of 280 slices. Before we can effectively use this fraction, we need to simplify it to its lowest terms. This makes the fraction easier to understand and work with in calculations. Understanding this fraction also involves grasping the concepts of ratios, proportions, and percentages, all essential components of basic mathematics and numerous real-world applications.
Step-by-Step Simplification of 80/280
Simplifying a fraction means reducing it to its simplest form by finding the greatest common divisor (GCD) of both the numerator (80) and the denominator (280). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
-
Find the factors of 80: The factors of 80 are 1, 2, 4, 5, 8, 10, 16, 20, 40, and 80.
-
Find the factors of 280: The factors of 280 are 1, 2, 4, 5, 7, 8, 10, 14, 20, 28, 35, 40, 56, 70, 140, and 280.
-
Identify the Greatest Common Divisor (GCD): By comparing the lists, we see that the largest number that divides both 80 and 280 is 40. Therefore, the GCD of 80 and 280 is 40.
-
Divide both the numerator and the denominator by the GCD: Divide both 80 and 280 by 40:
80 ÷ 40 = 2 280 ÷ 40 = 7
Therefore, the simplified fraction is 2/7. This means that 80/280 is equivalent to 2/7; they represent the same proportion or ratio.
Converting 80/280 (or 2/7) to a Decimal
To convert the simplified fraction 2/7 to a decimal, we divide the numerator (2) by the denominator (7):
2 ÷ 7 ≈ 0.2857
This decimal is a repeating decimal, meaning the digits after the decimal point repeat infinitely (0.285714285714...). For most practical purposes, rounding to a certain number of decimal places is sufficient. For example, rounding to two decimal places gives us 0.29. Understanding the concept of repeating decimals is crucial for working with fractions that don't result in terminating decimals.
Mathematical Explanation: Prime Factorization and GCD
The process of finding the GCD can be further elucidated using prime factorization. Prime factorization involves expressing a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 80: 2 x 2 x 2 x 2 x 5 = 2<sup>4</sup> x 5
- Prime factorization of 280: 2 x 2 x 2 x 5 x 7 = 2<sup>3</sup> x 5 x 7
The GCD is found by identifying the common prime factors raised to the lowest power. In this case, both numbers share 2<sup>3</sup> and 5. Therefore, the GCD is 2<sup>3</sup> x 5 = 8 x 5 = 40. This method is particularly useful when dealing with larger numbers where identifying the GCD by simply listing factors becomes cumbersome.
Real-World Applications of Fractions Like 80/280
Fractions are fundamental to numerous real-world applications across various fields:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Understanding fractions is crucial for accurate measurements and achieving the desired results.
-
Construction and Engineering: Precise measurements and calculations are essential in construction and engineering projects. Fractions play a vital role in ensuring accuracy and structural integrity.
-
Finance and Budgeting: Fractions are used extensively in finance to represent portions of budgets, investments, and debts.
-
Data Analysis and Statistics: Fractions and percentages (which are directly derived from fractions) are fundamental to interpreting and presenting data in various analyses and statistical reports.
-
Probability and Statistics: Calculating probabilities and analyzing statistical data frequently involves working with fractions to represent the likelihood of events.
-
Science and Measurement: In scientific experiments and measurements, fractions are used to express precise values and proportions.
The fraction 80/280, or its simplified equivalent 2/7, can represent any situation where a portion of a whole is involved. For example, if a school has 280 students and 80 of them participate in a particular club, then 2/7 of the students are members of that club.
Understanding Ratios and Proportions
The fraction 80/280 can also be understood as a ratio. A ratio compares two quantities. In this case, the ratio is 80:280, which simplifies to 2:7. This indicates that for every 2 parts of one quantity, there are 7 parts of another.
Proportions involve comparing two ratios. For example, if we have the proportion 2/7 = x/14, we can solve for x to find an equivalent ratio. In this case, x = 4. This signifies that if we have a total of 14 parts, 4 of them would represent the same proportion as 2 out of 7.
Frequently Asked Questions (FAQ)
-
Q: Can I simplify 80/280 in a different way? A: While the method above using the GCD of 40 is the most efficient, you can also simplify it step-by-step by dividing both numerator and denominator by common factors until you reach the simplest form. For example, you could first divide by 10 (resulting in 8/28) and then by 4 (resulting in 2/7).
-
Q: Why is it important to simplify fractions? A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It also reduces the risk of errors in more complex mathematical operations.
-
Q: What if I round the decimal 0.2857 to 0.29? Will it affect my calculations? A: Rounding introduces a small error. The impact of this error depends on the context of the calculation. For many applications, rounding to a few decimal places is sufficient and acceptable. However, for situations requiring high precision, it's crucial to retain more decimal places or work with the fraction in its simplified form.
-
Q: Are there other methods to convert a fraction to a decimal? A: Yes, you can use a calculator, or you can utilize long division to manually divide the numerator by the denominator.
-
Q: How do I convert the decimal back to a fraction? A: To convert a decimal like 0.2857 back to a fraction, you can express it as 2857/10000. However, this would not be the simplified fraction (2/7).
Conclusion: Mastering Fractions for Everyday Life
The fraction 80/280, when simplified to 2/7, illustrates fundamental concepts in mathematics – simplification, decimal conversion, ratios, and proportions. Understanding these concepts is not only crucial for academic success but also for effectively navigating numerous real-world situations requiring precise calculations and proportional reasoning. By mastering the techniques presented in this article, you'll enhance your mathematical skills and gain confidence in tackling similar problems involving fractions. Remember, the ability to simplify fractions and convert them into decimals is a valuable skill that will benefit you across various aspects of your life.
Latest Posts
Latest Posts
-
G And R
Sep 20, 2025
-
Ml3 To M3
Sep 20, 2025
-
Excel Radar Chart
Sep 20, 2025
-
Ts 400 Stihl
Sep 20, 2025
-
178 Lbs Kg
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 80 Of 280 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.