75 Of 45
interactiveleap
Sep 14, 2025 · 5 min read
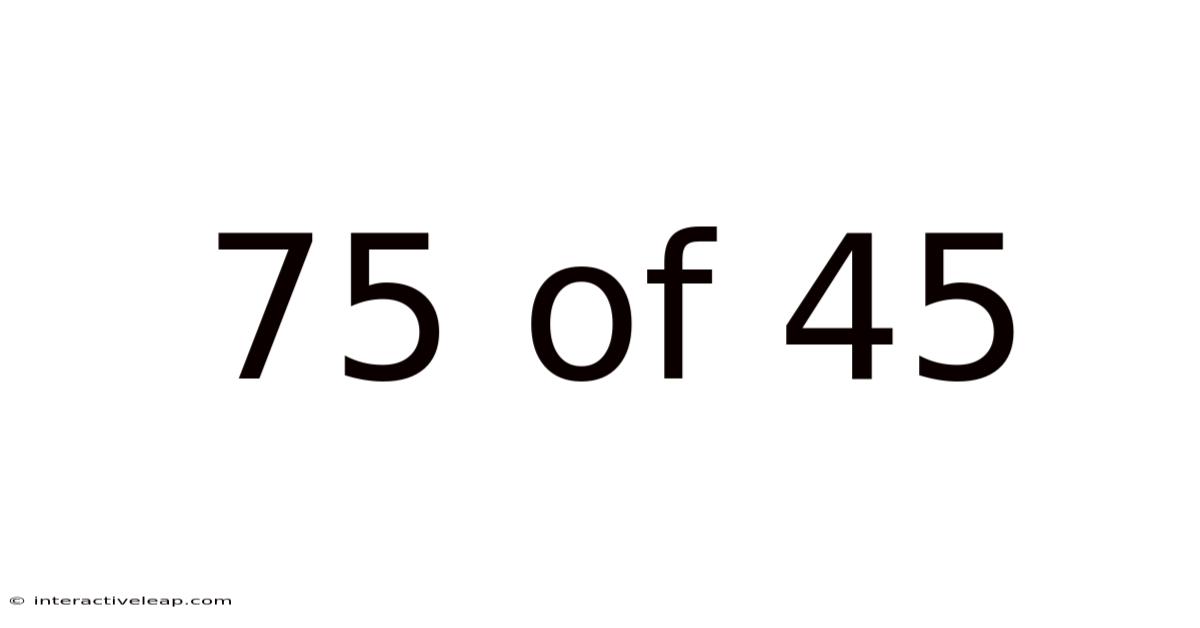
Table of Contents
Decoding the Fraction: Understanding 75/45 and its Implications
The seemingly simple fraction 75/45 might appear straightforward at first glance, but it opens a door to exploring fundamental concepts in mathematics, particularly fractions, ratios, and percentages. This article will delve into a comprehensive analysis of 75/45, exploring its simplification, its decimal and percentage equivalents, real-world applications, and potential misconceptions. We'll also touch upon the broader mathematical principles it exemplifies.
Introduction: What is 75/45?
75/45 represents a fraction where 75 is the numerator (the top number) and 45 is the denominator (the bottom number). This fraction describes a part-to-whole relationship, indicating 75 parts out of a total of 45 parts. This immediately suggests that the fraction is improper, meaning the numerator is larger than the denominator. Improper fractions often represent quantities greater than one whole. Understanding this foundational concept is crucial before proceeding. The keywords associated with this topic include fraction simplification, improper fractions, decimal conversion, percentage calculation, and ratio analysis.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve into further calculations, simplifying the fraction is crucial. Simplifying, also known as reducing, means finding an equivalent fraction with smaller numbers. This is achieved by finding the greatest common divisor (GCD) of both the numerator and the denominator. The GCD is the largest number that divides both 75 and 45 without leaving a remainder.
Let's find the GCD of 75 and 45 using the prime factorization method:
- Prime factorization of 75: 3 x 5 x 5 = 3 x 5²
- Prime factorization of 45: 3 x 3 x 5 = 3² x 5
The common factors are 3 and 5. The lowest power of 3 is 3¹, and the lowest power of 5 is 5¹. Therefore, the GCD is 3 x 5 = 15.
Now, we divide both the numerator and the denominator by the GCD:
75 ÷ 15 = 5 45 ÷ 15 = 3
Therefore, the simplified fraction is 5/3. This is still an improper fraction, indicating a value greater than 1.
Converting to Decimal and Percentage: Unveiling the Numerical Value
To gain a clearer understanding of the value of 75/45 (or its simplified form, 5/3), we can convert it into a decimal and a percentage.
-
Decimal Conversion: To convert a fraction to a decimal, simply divide the numerator by the denominator: 5 ÷ 3 = 1.666... This is a repeating decimal, often represented as 1.6̅6̅.
-
Percentage Conversion: To convert a decimal to a percentage, multiply by 100: 1.666... x 100 = 166.666...% Again, this is a repeating percentage. We can round this to a suitable level of precision, such as 166.67%.
Therefore, 75/45 is equivalent to 1.666... (or approximately 1.67) as a decimal and 166.666...% (or approximately 166.67%) as a percentage.
Real-World Applications: Illustrating the Fraction in Context
The fraction 75/45 can represent numerous real-world scenarios. Imagine:
-
Sharing Resources: If you have 75 cookies to share among 45 people, each person would receive 75/45 = 5/3 cookies, or approximately 1.67 cookies.
-
Test Scores: If you answered 75 questions correctly out of a total of 45 questions on a test (perhaps a multiple choice test with bonus questions), your score would be 75/45 = 5/3 or approximately 166.67%, indicating you performed significantly above expectations, likely due to bonus questions or extra credit.
-
Project Completion: If a project required 45 units of work and 75 units were completed, the project completion rate is 75/45 = 5/3 or approximately 166.67%. This suggests the project is significantly over-completed.
These examples highlight the practical implications of understanding and interpreting improper fractions.
Understanding Ratios: A Deeper Mathematical Perspective
The fraction 75/45 can also be interpreted as a ratio: 75:45. This ratio indicates a relationship between two quantities. Simplifying the ratio, just like simplifying the fraction, yields 5:3. This simplified ratio suggests that for every 5 units of one quantity, there are 3 units of another.
Ratios are fundamental in various fields, including:
- Scale Models: Architects and engineers use ratios to create scale models of buildings and structures.
- Mixing Ingredients: Recipes often involve ratios of ingredients, for instance, a 2:1 ratio of flour to sugar.
- Financial Analysis: Ratios are extensively used in financial analysis to assess the financial health of companies.
Addressing Common Misconceptions:
A common mistake is misinterpreting improper fractions. Students may incorrectly believe that a fraction must always be less than 1. Understanding that the numerator can be larger than the denominator is crucial for grasping the concept of improper fractions and their representation of values greater than 1.
Another misconception involves simplification. Students might attempt to simplify by subtracting instead of dividing. Remember, simplification involves dividing both the numerator and the denominator by their greatest common divisor.
Frequently Asked Questions (FAQ)
-
Q: Why is 75/45 an improper fraction? A: Because the numerator (75) is greater than the denominator (45).
-
Q: What is the simplified form of 75/45? A: 5/3
-
Q: How do I convert 75/45 to a decimal? A: Divide the numerator (75) by the denominator (45).
-
Q: How do I convert 75/45 to a percentage? A: Convert the fraction to a decimal and then multiply by 100.
-
Q: Can a fraction be greater than 1? A: Yes, improper fractions are greater than 1.
Conclusion: Beyond the Numbers
The seemingly simple fraction 75/45 provides a rich learning opportunity, extending beyond basic arithmetic. Understanding its simplification, its decimal and percentage equivalents, its representation as a ratio, and its real-world applications reinforces fundamental mathematical concepts. By addressing common misconceptions and exploring the broader implications, we develop a more profound understanding of fractions and their significance in various aspects of life. The journey from 75/45 to its simplified form, 5/3, and further to its decimal and percentage equivalents, underscores the importance of mathematical precision and the interconnectedness of various mathematical concepts. This understanding extends beyond simple calculation, providing a solid foundation for more advanced mathematical explorations.
Latest Posts
Latest Posts
-
10 Of 3500
Sep 14, 2025
-
Wishes Are Horses
Sep 14, 2025
-
X 2 17
Sep 14, 2025
-
32cm To Inches
Sep 14, 2025
-
Briefing Note Example
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.