X 2 17
interactiveleap
Sep 14, 2025 · 6 min read
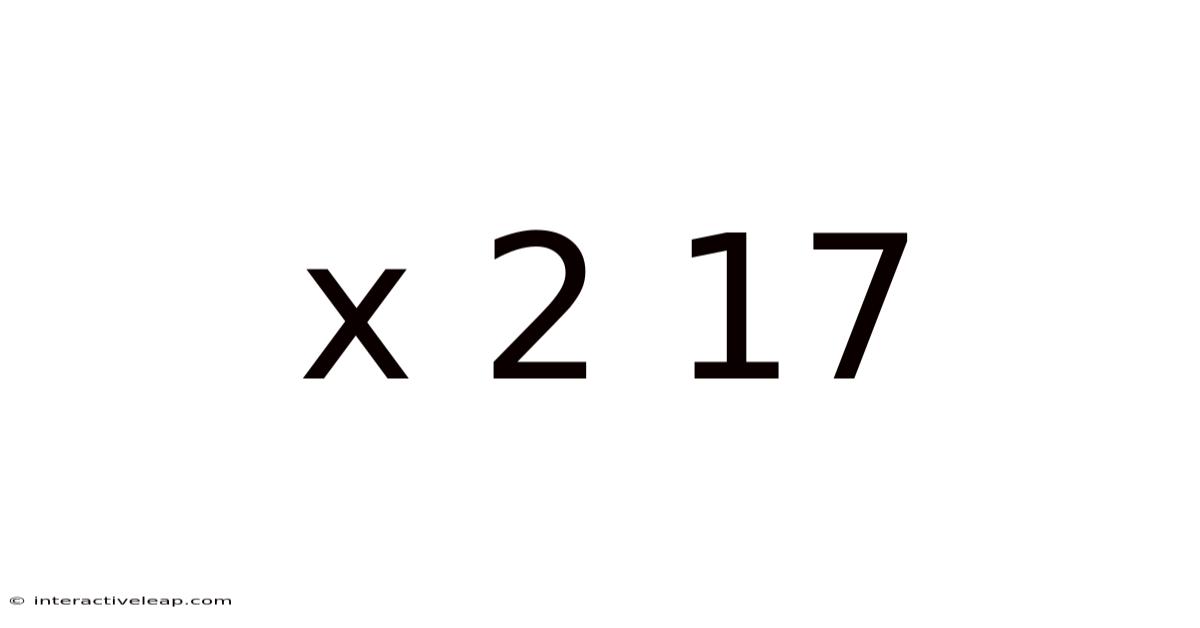
Table of Contents
Decoding x² + 17: A Deep Dive into Quadratic Equations and Number Theory
The seemingly simple expression x² + 17 might appear innocuous at first glance. However, this quadratic equation opens a door to a fascinating exploration of number theory, revealing surprising patterns and connections within the seemingly abstract world of mathematics. This article will delve into the properties of x² + 17, exploring its behavior for different integer values of x, analyzing its relationship to prime numbers, and discussing its significance within broader mathematical concepts. We'll also address frequently asked questions and provide a concise summary of key takeaways.
Introduction: Exploring the Landscape of x² + 17
The quadratic expression x² + 17 is a fundamental building block in algebra and number theory. Understanding its behavior for various integer values of x unveils rich mathematical insights. This expression, seemingly simple, exhibits intriguing patterns when examining its output for consecutive integers. We'll analyze these patterns, exploring the distribution of prime numbers generated by this expression and connecting these observations to deeper concepts within number theory. Ultimately, this investigation aims to highlight the interconnectedness of seemingly disparate mathematical fields.
Exploring Integer Values of x:
Let's begin by evaluating x² + 17 for several integer values of x:
- x = 0: 0² + 17 = 17 (a prime number)
- x = 1: 1² + 17 = 18 (not a prime number)
- x = 2: 2² + 17 = 21 (not a prime number)
- x = 3: 3² + 17 = 26 (not a prime number)
- x = 4: 4² + 17 = 33 (not a prime number)
- x = 5: 5² + 17 = 42 (not a prime number)
- x = 6: 6² + 17 = 53 (a prime number)
- x = 7: 7² + 17 = 66 (not a prime number)
- x = 8: 8² + 17 = 81 (not a prime number)
- x = 9: 9² + 17 = 98 (not a prime number)
- x = 10: 10² + 17 = 117 (not a prime number)
Initially, the results appear somewhat random. However, a deeper analysis reveals patterns related to the distribution of prime numbers. Notice that for some values of x, the expression yields prime numbers, while for others, it produces composite numbers. This irregular behavior is a characteristic feature of many number-theoretic functions.
The Hunt for Prime Numbers:
One of the most fascinating aspects of x² + 17 is its ability to generate prime numbers for certain values of x. The question arises: Are there infinitely many values of x for which x² + 17 is a prime number? This question connects directly to one of the most fundamental unsolved problems in mathematics: the distribution of prime numbers.
While there's no simple formula to predict which values of x will produce prime numbers, we can observe that the expression frequently generates composite numbers. The relative frequency of prime outputs decreases as x increases, suggesting a potentially finite number of prime outputs. This observation highlights the unpredictable nature of prime number distribution, a core challenge in number theory.
Connecting to Quadratic Residues:
The expression x² + 17 can be analyzed using the concept of quadratic residues. A quadratic residue modulo n is an integer a such that there exists an integer x satisfying x² ≡ a (mod n). In simpler terms, it's a number that can be expressed as the square of another number modulo n.
Analyzing x² + 17 in terms of quadratic residues reveals additional insights into the patterns of prime and composite outputs. For instance, investigating the values for which x² + 17 is a quadratic residue modulo various prime numbers can provide further understanding of its behavior. This exploration requires a more advanced understanding of modular arithmetic and number theory concepts.
Beyond the Integers: Exploring Real and Complex Numbers
While our focus has been on integer values of x, the expression x² + 17 is well-defined for real and complex numbers as well. Extending the analysis to these number systems opens up new avenues of investigation.
For real numbers, x² + 17 represents a parabola that opens upwards, with a vertex at (0, 17). Its properties as a continuous function are quite different from its discrete behavior for integer values of x. Similarly, in the complex plane, x² + 17 describes a surface with interesting geometric properties. These extensions provide a broader context for understanding the expression's overall behavior.
The Role of x² + 17 in Number Theory:
x² + 17 serves as a valuable example in illustrating several key concepts in number theory:
- Prime Number Distribution: The seemingly random generation of prime and composite numbers underscores the challenges in predicting prime distribution.
- Quadratic Residues: Analyzing the expression using quadratic residues provides a more structured approach to understanding its behavior modulo different integers.
- Diophantine Equations: If we set x² + 17 equal to another expression, we'd have a Diophantine equation, which is a type of equation where solutions are restricted to integers. Solving these equations can be exceptionally challenging.
- Polynomial Functions: x² + 17 is a simple polynomial function, and exploring its behavior helps to build intuition about the properties of polynomial functions in general.
Frequently Asked Questions (FAQ):
- Is x² + 17 always a prime number? No, x² + 17 is a prime number for some integer values of x, but not for all.
- How can I predict when x² + 17 will be prime? There's no simple formula or algorithm to predict exactly when x² + 17 will produce a prime number. This highlights the complexity of prime number distribution.
- What are the practical applications of studying x² + 17? While direct applications might not be immediately apparent, studying this expression contributes to our broader understanding of number theory, which underpins many aspects of cryptography and computer science. It helps build foundational mathematical skills crucial for advanced studies.
- Are there similar expressions with similar properties? Yes, there are other polynomial expressions that exhibit similar behavior in terms of generating prime numbers for certain integer inputs. These expressions often play a role in exploring conjectures and unsolved problems within number theory.
Conclusion: A Journey into the Heart of Mathematics
Our investigation into the expression x² + 17 has revealed a rich tapestry of mathematical concepts, demonstrating the interconnectedness of seemingly disparate areas like algebra and number theory. While the expression itself may appear simple, its study reveals the complexities inherent in understanding prime number distribution and the challenges in predicting the behavior of even elementary mathematical functions. The exploration of x² + 17 serves as a valuable illustration of the beauty and intricacy of mathematics, highlighting the ongoing quest for deeper understanding within this fundamental field of human knowledge. The unexpected patterns and complexities associated with this seemingly simple expression underscore the enduring fascination and challenge of mathematical exploration. The journey from a simple quadratic equation to a deeper understanding of prime numbers and quadratic residues is a testament to the power and elegance of mathematics. It’s a journey that invites further investigation and highlights the boundless possibilities within the mathematical universe.
Latest Posts
Latest Posts
-
Megalodon Comparison Size
Sep 14, 2025
-
Autumn In Spanish
Sep 14, 2025
-
20 Of 380
Sep 14, 2025
-
Factorise 7y 21
Sep 14, 2025
-
Decimal Of 15
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 2 17 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.