75 Of 32
interactiveleap
Sep 20, 2025 · 5 min read
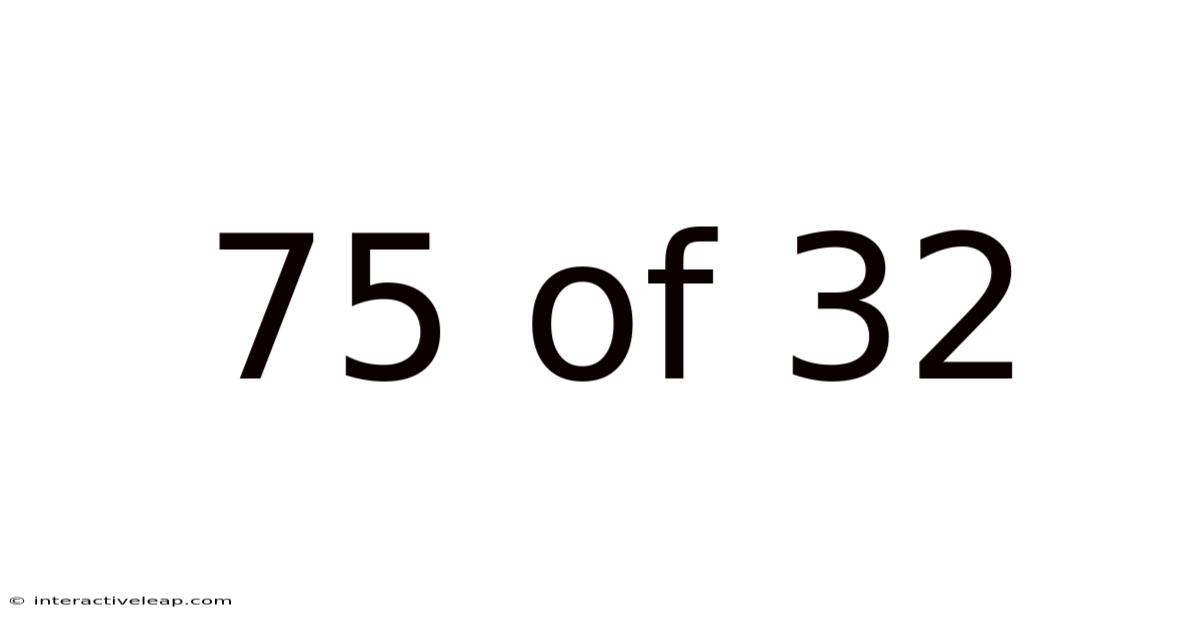
Table of Contents
Decoding the Fraction: 75/32 and its Implications
Understanding fractions is fundamental to mathematics and its various applications in everyday life. This article delves into the seemingly simple fraction 75/32, exploring its various representations, calculations, and implications within different mathematical contexts. We'll move beyond simple reduction and explore its decimal equivalent, its application in measurement and problem-solving, and discuss its significance in understanding broader mathematical concepts. This comprehensive guide will equip you with a thorough understanding of this fraction and its place within the larger world of numbers.
Introduction to 75/32: An Improper Fraction
The fraction 75/32 is an improper fraction, meaning the numerator (75) is larger than the denominator (32). This immediately tells us that the fraction represents a value greater than one. Improper fractions are useful for representing quantities that exceed a whole unit, and they are often a precursor to mixed numbers. Understanding this fundamental characteristic is crucial before proceeding to more advanced manipulations.
Converting to a Mixed Number
One of the first steps in working with improper fractions like 75/32 is to convert it into a mixed number. A mixed number combines a whole number and a proper fraction. To do this, we perform division:
75 ÷ 32 = 2 with a remainder of 11
This means 75/32 can be expressed as 2 11/32. This representation is often easier to visualize and understand in practical applications, as it clearly shows that the value is two whole units and a fraction of another.
Decimal Representation of 75/32
Converting the fraction to its decimal equivalent is another valuable step. This provides a different perspective on the value and facilitates calculations involving decimals. To find the decimal representation, we simply divide the numerator by the denominator:
75 ÷ 32 ≈ 2.34375
Therefore, 75/32 is approximately equal to 2.34375. The decimal form can be particularly useful when working with calculators or computer programs that primarily use decimal notation.
Visualizing 75/32
To further solidify our understanding, let's visualize 75/32. Imagine you have 75 identical objects, and you want to divide them into groups of 32. You would be able to create two complete groups, with 11 objects remaining. This perfectly mirrors the mixed number representation of 2 11/32. This visual representation can be helpful for grasping the concept, especially when teaching younger students.
Applications of 75/32 in Real-World Scenarios
While it might seem like an abstract concept, 75/32 has practical applications in various real-world scenarios. Consider these examples:
- Measurement: Imagine you are measuring a length and your ruler shows a measurement of 75/32 inches. This clearly indicates a length slightly over 2 and a quarter inches.
- Resource Allocation: You have 75 units of a resource (e.g., liters of water, kilograms of material) that need to be distributed evenly among 32 individuals. The fraction helps determine the amount each person receives (approximately 2.34 units).
- Data Analysis: In statistical analysis, you might encounter a ratio or proportion expressed as 75/32. Converting it to a decimal or percentage helps in interpreting the data and drawing conclusions.
Working with 75/32 in Calculations
Let's explore how 75/32 interacts in various mathematical operations:
- Addition/Subtraction: When adding or subtracting fractions, ensure they have a common denominator. For example, adding 75/32 to another fraction would require finding a common denominator before proceeding.
- Multiplication: Multiplying 75/32 by another fraction involves multiplying the numerators and denominators separately. Simplification might be needed afterward.
- Division: Dividing by 75/32 is equivalent to multiplying by its reciprocal (32/75). This is a fundamental concept in fraction manipulation.
Further Mathematical Exploration: Percentages and Ratios
75/32 can also be expressed as a percentage. To do this, we convert the decimal equivalent (2.34375) to a percentage by multiplying by 100:
2.34375 * 100 = 234.375%
This representation highlights that 75/32 is 234.375% of the denominator (32).
Furthermore, 75/32 represents a ratio of 75 to 32. This ratio can be used to compare quantities or to scale values proportionally. Understanding this aspect can be critical in various fields like engineering, architecture, and finance.
Frequently Asked Questions (FAQs)
Q: Is 75/32 a rational number?
A: Yes, 75/32 is a rational number because it can be expressed as a fraction of two integers.
Q: How do I simplify 75/32?
A: 75/32 is already in its simplest form because the greatest common divisor of 75 and 32 is 1. Simplification is only possible if the numerator and denominator share a common factor greater than 1.
Q: What is the reciprocal of 75/32?
A: The reciprocal of 75/32 is 32/75. Reciprocals are used in division and other mathematical operations.
Q: Can 75/32 be expressed as a terminating decimal?
A: Yes, 75/32 can be expressed as a terminating decimal (2.34375) because the denominator (32) only has factors of 2. If the denominator contained any prime factors other than 2 and 5, the decimal representation would be non-terminating (repeating).
Conclusion: Mastering the Fraction 75/32
Understanding the fraction 75/32 extends beyond simple numerical manipulation. It's about grasping the fundamental concepts of fractions, mixed numbers, decimals, percentages, and ratios. By exploring its various representations and applications, we have not only solved the immediate problem of understanding this specific fraction but also gained a deeper appreciation of the broader mathematical principles it embodies. The ability to confidently work with fractions like 75/32 is essential for success in many areas of life, from basic arithmetic to advanced mathematical problem-solving. The insights gained from this analysis will empower you to confidently approach similar fractions and further your mathematical understanding. This comprehensive exploration should serve as a robust foundation for tackling more complex fractional calculations and mathematical concepts in the future.
Latest Posts
Latest Posts
-
Mj In J
Sep 20, 2025
-
10000km In Miles
Sep 20, 2025
-
25 Of 3600
Sep 20, 2025
-
X 3 X
Sep 20, 2025
-
18 5cm To Inches
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.