75 Of 1500
interactiveleap
Sep 23, 2025 · 5 min read
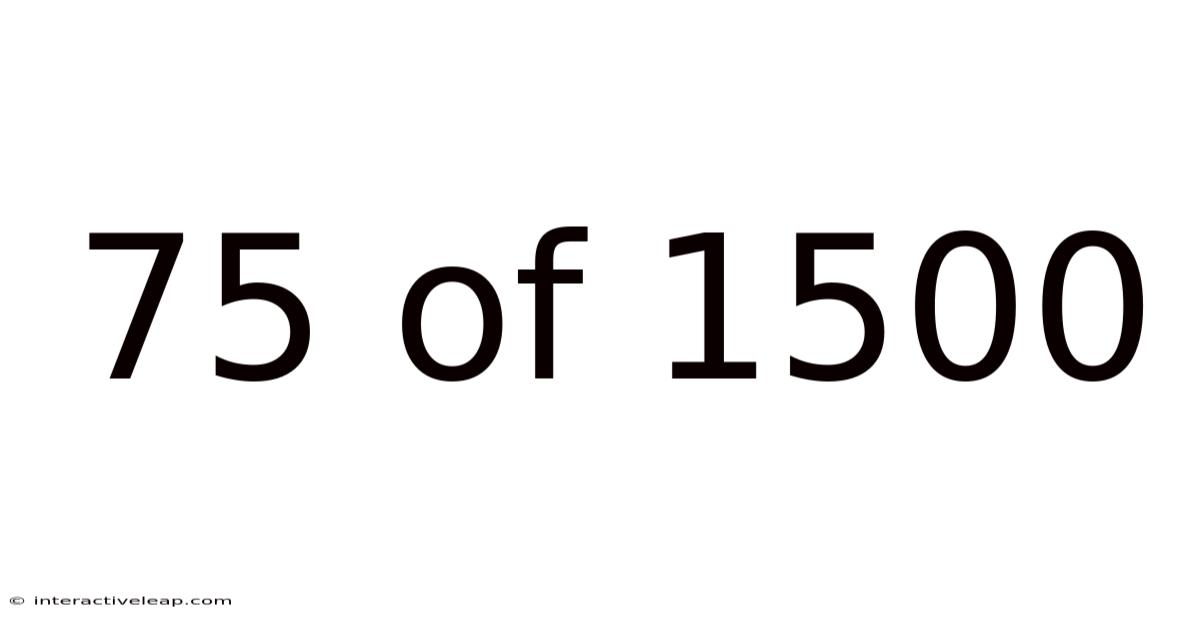
Table of Contents
Decoding the Fraction: Understanding 75 out of 1500
Understanding fractions can seem daunting, especially when dealing with larger numbers like 75 out of 1500. This article will demystify this fraction, explaining not only its simplified form and decimal equivalent but also exploring various contexts where such calculations are crucial. We'll delve into the mathematical processes, practical applications, and even touch upon the importance of understanding ratios and proportions in everyday life. This guide aims to provide a comprehensive understanding of 75/1500, leaving you confident in handling similar fractional calculations in the future.
Simplifying the Fraction: Finding the Simplest Form
The fraction 75/1500 represents 75 parts out of a total of 1500 parts. To understand it better, we need to simplify it to its lowest terms. This means finding the greatest common divisor (GCD) of both the numerator (75) and the denominator (1500) and dividing both by it.
The prime factorization of 75 is 3 x 5 x 5 (or 3 x 5²). The prime factorization of 1500 is 2 x 2 x 3 x 5 x 5 x 5 (or 2² x 3 x 5³).
The common factors are 3 x 5 x 5 = 75. Therefore, the GCD of 75 and 1500 is 75.
Dividing both the numerator and the denominator by 75, we get:
75 ÷ 75 = 1 1500 ÷ 75 = 20
Therefore, the simplified form of 75/1500 is 1/20. This means that 75 out of 1500 is equivalent to 1 out of 20. This simplified fraction is much easier to understand and work with.
Converting to a Decimal: Expressing the Fraction as a Percentage
Converting a fraction to a decimal is a straightforward process. We simply divide the numerator by the denominator. In this case:
1 ÷ 20 = 0.05
Therefore, 75/1500 is equal to 0.05 as a decimal.
To express this as a percentage, we multiply the decimal by 100:
0.05 x 100 = 5%
So, 75 out of 1500 represents 5%.
Real-World Applications: Where This Fraction Might Appear
Understanding fractions like 75/1500 isn't just about abstract mathematics; it has practical applications in numerous fields:
-
Grade Calculations: Imagine a student scoring 75 out of 1500 points on a cumulative exam across all subjects. Understanding the fraction helps determine their overall percentage score (5%), which can be crucial for grade determination.
-
Survey Results: If 75 out of 1500 respondents to a survey answered "yes" to a particular question, the fraction represents the proportion of "yes" responses. This data is vital for analyzing public opinion or consumer behavior.
-
Inventory Management: A warehouse might have 1500 items, with 75 of them being defective. The fraction allows for the calculation of the defect rate (5%), which is critical for quality control and inventory management strategies.
-
Financial Analysis: In finance, ratios are extensively used. For example, if a company has a total revenue of 1500 units and 75 of those units were losses, understanding the ratio helps analyze profitability and risk.
-
Sports Statistics: In baseball, a player's batting average is a fraction. If a player has 75 hits out of 1500 at-bats, their batting average is 0.05 or 5%. While this example is a small scale, many sports analytics involve fractions for calculating performance metrics.
Beyond the Basics: Exploring Ratios and Proportions
Understanding 75/1500 goes beyond simply simplifying the fraction and converting it to a decimal or percentage. It highlights the broader concept of ratios and proportions.
A ratio is a comparison of two quantities. In this case, the ratio is 75:1500, representing the relationship between the number of successful events (75) and the total number of events (1500).
A proportion is a statement that two ratios are equal. For instance, we can say that the ratio 75:1500 is proportional to the ratio 1:20, because they represent the same relationship. Understanding proportions allows us to solve for unknown quantities in similar scenarios. For example, if we know that 1 out of 20 students passed a test, and we have 300 students, we can use proportions to determine how many passed:
1/20 = x/300
Solving for x (cross-multiplying):
20x = 300 x = 15
Therefore, 15 out of 300 students passed the test.
Further Explorations: Advanced Applications
The principles involved in understanding 75/1500 extend to more complex mathematical concepts:
-
Percentages and Discounts: The 5% calculated from 75/1500 is frequently used in calculating discounts, tax rates, interest rates, and profit margins.
-
Statistical Analysis: In statistics, this type of fractional calculation is fundamental to calculating probabilities, analyzing data distributions, and performing hypothesis testing.
-
Probability Theory: Understanding the likelihood of events occurring is a cornerstone of probability theory, and fractions like 75/1500 help to understand this likelihood.
-
Engineering and Architecture: Proportions are essential in engineering and architecture to maintain scale and accuracy in designs and blueprints.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 75/1500?
A: The simplest form of 75/1500 is 1/20.
Q: What is the decimal equivalent of 75/1500?
A: The decimal equivalent of 75/1500 is 0.05.
Q: What is the percentage equivalent of 75/1500?
A: The percentage equivalent of 75/1500 is 5%.
Q: How do I convert a fraction to a decimal?
A: To convert a fraction to a decimal, divide the numerator by the denominator.
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100.
Q: What is the difference between a ratio and a proportion?
A: A ratio compares two quantities, while a proportion states that two ratios are equal.
Conclusion: Mastering Fractions for a Brighter Future
Understanding fractions, even seemingly complex ones like 75/1500, is a crucial skill applicable to various aspects of life. By simplifying the fraction, converting it to a decimal and percentage, and understanding its application in ratios and proportions, you equip yourself with a powerful tool for problem-solving in various fields. This knowledge empowers you not only to tackle academic challenges but also to make informed decisions in your personal and professional life. From calculating grades and analyzing survey data to understanding financial statements and navigating everyday situations, the ability to work with fractions is a fundamental skill that pays dividends. Remember that consistent practice and a willingness to explore further applications will solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
26 36 Simplified
Sep 23, 2025
-
49 X 12
Sep 23, 2025
-
49 3kg In Stone
Sep 23, 2025
-
Half Eleven Time
Sep 23, 2025
-
Port Udp 137
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 75 Of 1500 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.