49 X 12
interactiveleap
Sep 23, 2025 · 5 min read
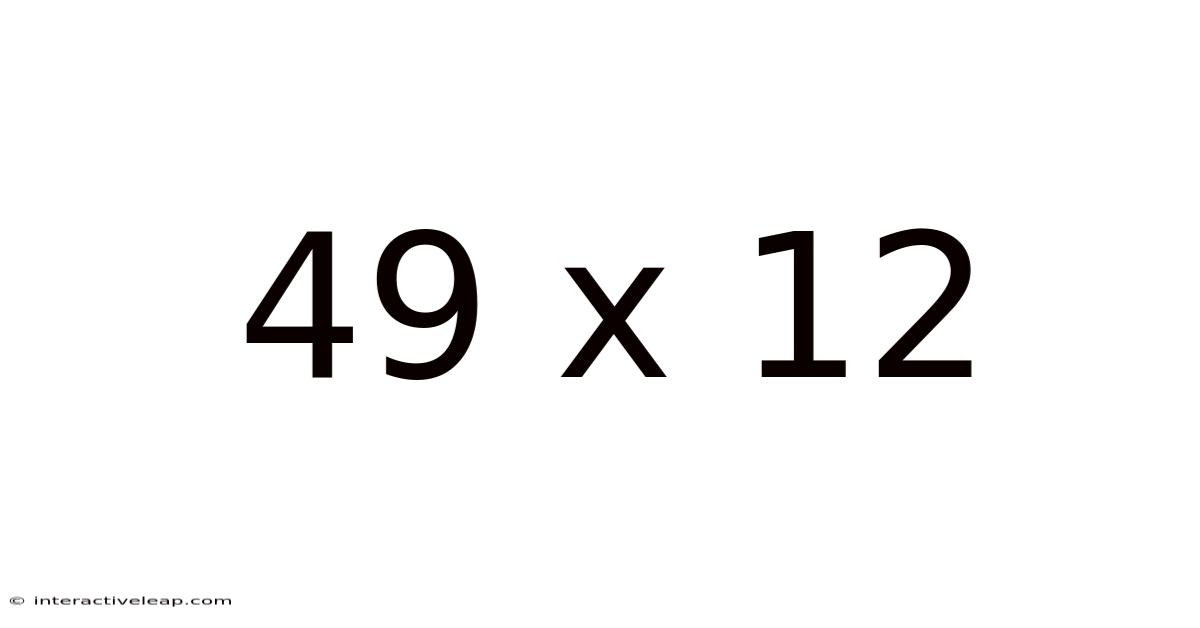
Table of Contents
Unpacking 49 x 12: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 49 x 12, transforming it into a gateway to understanding fundamental mathematical concepts and their real-world applications. We'll move beyond simply stating the answer, delving into various methods of solving this problem, exploring the underlying principles, and demonstrating its relevance in diverse contexts. This will cover everything from basic arithmetic to more advanced strategies and practical examples, making it a comprehensive guide suitable for learners of all levels.
Understanding the Fundamentals: What is Multiplication?
Multiplication is a fundamental arithmetic operation representing repeated addition. When we say 49 x 12, we're essentially asking: "What is the sum of twelve 49s?" This seemingly simple concept underpins countless calculations in various fields, from finance to engineering. Understanding its core principles is crucial for mastering more complex mathematical operations.
Methods for Solving 49 x 12: A Comparative Approach
There are several ways to solve 49 x 12, each offering a unique perspective on the problem and catering to different learning styles. Let's explore some common methods:
1. Standard Multiplication Algorithm
This is the most commonly taught method, involving breaking down the numbers into tens and units and performing a series of multiplications and additions.
- Step 1: Multiply 49 by 2 (the units digit of 12): 49 x 2 = 98. Write down 98.
- Step 2: Multiply 49 by 10 (the tens digit of 12): 49 x 10 = 490. Write this below 98, aligning the units digit with the tens digit of 98.
- Step 3: Add the results: 98 + 490 = 588
Therefore, 49 x 12 = 588. This method systematically breaks down the problem into smaller, manageable steps.
2. Distributive Property
The distributive property states that a(b + c) = ab + ac. We can apply this to solve 49 x 12 as follows:
- Rewrite 12 as 10 + 2: 49 x (10 + 2)
- Distribute 49: (49 x 10) + (49 x 2)
- Calculate: 490 + 98 = 588
This method highlights the underlying algebraic principles behind multiplication, demonstrating how it interacts with addition.
3. Mental Math Techniques
For those comfortable with mental arithmetic, several techniques can simplify the calculation:
- Breaking down the numbers: Think of 49 as 50 - 1. Then, 50 x 12 = 600, and subtract 12 (12 x 1) to get 588.
- Doubling and halving: Double 12 to get 24, and halve 49 to get 49/2 = 24.5. This approach is less straightforward for this specific problem but is useful for other multiplications.
4. Using a Calculator
While less instructive in terms of understanding the underlying mathematical principles, a calculator provides a quick and accurate solution. Simply input 49 x 12 and the answer, 588, appears instantly. This method is particularly helpful for larger or more complex calculations.
Beyond the Calculation: Real-World Applications of 49 x 12
While the act of multiplying 49 by 12 might seem abstract, its applications are surprisingly widespread. Let's explore some examples:
- Retail and Commerce: Imagine a retailer selling items priced at $49 each. If they sell 12 of these items, the total revenue is 49 x 12 = $588. This simple calculation is fundamental to inventory management and sales tracking.
- Construction and Engineering: Calculating the total area of a space often involves multiplication. For instance, a room measuring 49 feet by 12 feet has a total area of 588 square feet. This is crucial for planning material requirements and project costing.
- Data Analysis: In data analysis, multiplication is frequently used in calculations involving proportions, percentages, and scaling. If 49% of a sample of 12 individuals displayed a specific characteristic, the calculation 49/100 * 12 would be used to determine the number of individuals exhibiting that characteristic.
- Finance and Accounting: Calculating interest, discounts, or taxes often involves multiplication. For example, calculating a 12% commission on a sale of $49 would involve multiplying 0.12 x 49.
Expanding the Concept: Exploring Related Mathematical Concepts
Solving 49 x 12 opens doors to exploring related mathematical concepts:
- Factors and Multiples: Understanding the factors of 49 (1, 7, 49) and 12 (1, 2, 3, 4, 6, 12) provides insights into divisibility rules and prime factorization.
- Prime Numbers: Investigating the prime factorization of both 49 (7 x 7) and 12 (2 x 2 x 3) helps in understanding the building blocks of numbers.
- Order of Operations (PEMDAS/BODMAS): When dealing with more complex equations involving multiplication alongside other operations (addition, subtraction, division, exponents), understanding the order of operations is critical for obtaining the correct result.
Frequently Asked Questions (FAQ)
Q1: What are some alternative methods for solving 49 x 12 without using the standard algorithm?
A1: As discussed above, using the distributive property, mental math techniques (breaking down numbers or using doubling/halving), or a calculator are all viable alternatives.
Q2: Is there a shortcut for multiplying by 12?
A2: Yes, one shortcut involves multiplying by 10 and then adding twice the original number. For example, 49 x 12 = (49 x 10) + (49 x 2) = 490 + 98 = 588.
Q3: Why is understanding multiplication important?
A3: Multiplication is fundamental to various fields, enabling efficient calculations in areas like finance, engineering, science, and daily life. Mastering multiplication builds a strong foundation for more advanced mathematical concepts.
Q4: How can I improve my multiplication skills?
A4: Practice is key! Regularly working through multiplication problems, using different methods, and applying them to real-world scenarios will enhance your skills and understanding.
Conclusion: The Power of a Simple Calculation
The seemingly simple calculation 49 x 12 serves as a powerful illustration of fundamental mathematical principles and their practical applications. By exploring different methods of solving this problem, we've uncovered deeper insights into multiplication, its underlying logic, and its widespread relevance in various domains. Remember, mastering basic arithmetic isn't just about getting the right answer; it's about understanding the underlying concepts and applying that knowledge to solve real-world problems effectively. This exploration of 49 x 12 is a testament to the power of seemingly simple calculations and the importance of understanding the fundamentals of mathematics. From understanding the distributive property to applying mental math tricks, this journey emphasizes that mathematics isn't just about numbers; it's about problem-solving, critical thinking, and the ability to translate abstract concepts into practical solutions. The next time you encounter a multiplication problem, remember the depth and breadth that can be uncovered, even from something as seemingly basic as 49 x 12.
Latest Posts
Latest Posts
-
60divided By 4
Sep 23, 2025
-
Dividing Into Ratios
Sep 23, 2025
-
Favouritism Towards Relatives
Sep 23, 2025
-
50 Of 32
Sep 23, 2025
-
Human Firewall Meaning
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 49 X 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.