60divided By 4
interactiveleap
Sep 23, 2025 · 6 min read
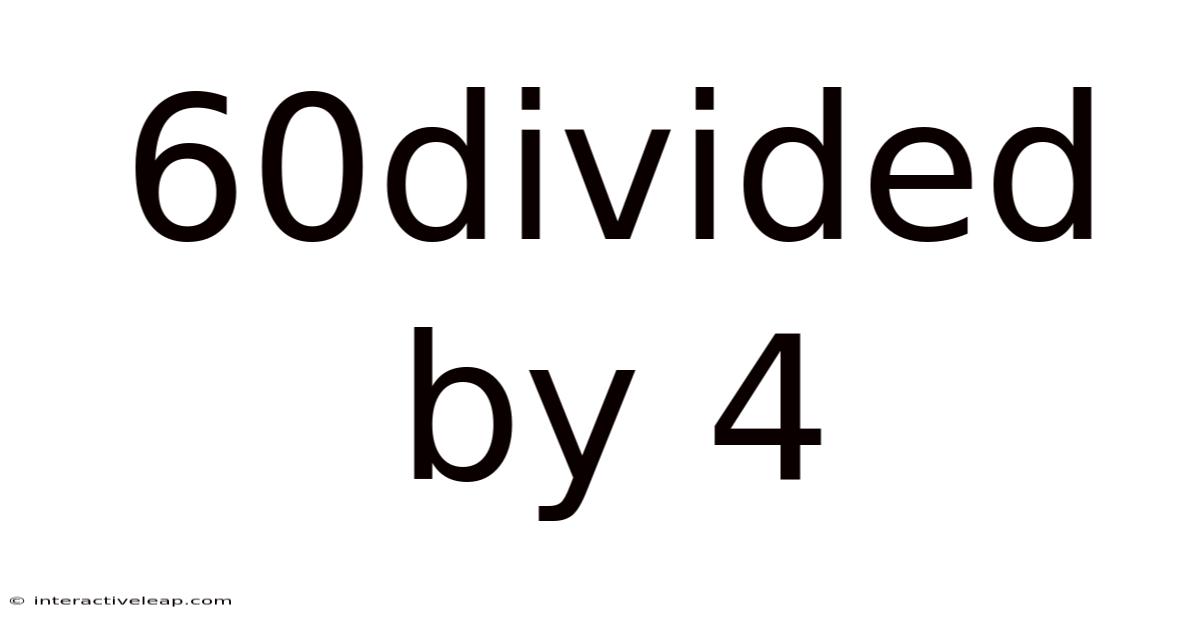
Table of Contents
Unveiling the Simplicity and Power of 60 Divided by 4: A Deep Dive into Division
Meta Description: Learn the simple solution to 60 divided by 4, explore various methods for solving division problems, and discover the underlying mathematical concepts. This comprehensive guide delves into different approaches, including long division, mental math techniques, and real-world applications, making division accessible to all.
The seemingly simple question, "What is 60 divided by 4?", opens the door to a world of mathematical understanding. While the answer itself is readily available – 15 – the journey to arrive at that answer offers valuable insights into fundamental mathematical operations and their practical applications. This article will not only provide the solution but also explore multiple methods for solving the problem, delve into the underlying mathematical principles, and demonstrate the relevance of division in everyday life.
Understanding Division: The Foundation
Before diving into the specific calculation of 60 divided by 4, let's establish a firm understanding of what division represents. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts or groups. In the expression 60 ÷ 4 (or 60/4), we're asking: "If we have 60 items, and we want to divide them into 4 equal groups, how many items will be in each group?"
Method 1: Long Division – A Step-by-Step Approach
Long division is a systematic method for solving division problems, particularly those involving larger numbers. It's a powerful tool that builds a solid foundation for understanding the process of division. Here's how to solve 60 ÷ 4 using long division:
-
Set up the problem: Write the dividend (60) inside the long division symbol (⟌) and the divisor (4) outside.
4 ⟌ 60 -
Divide the first digit: Divide the first digit of the dividend (6) by the divisor (4). 6 divided by 4 is 1 with a remainder of 2. Write the quotient (1) above the 6.
1 4 ⟌ 60 -
Bring down the next digit: Bring down the next digit of the dividend (0) next to the remainder (2), forming the number 20.
1 4 ⟌ 60 20 -
Divide again: Divide 20 by 4. 20 divided by 4 is 5 with no remainder. Write the quotient (5) above the 0.
15 4 ⟌ 60 20 20 -- 0 -
The result: The final quotient is 15. Therefore, 60 divided by 4 is 15.
Method 2: Repeated Subtraction – A Visual Approach
Repeated subtraction offers a more visual and intuitive method for understanding division, especially for smaller numbers. It involves repeatedly subtracting the divisor from the dividend until you reach zero or a remainder smaller than the divisor.
-
Start with the dividend: Begin with the dividend, 60.
-
Repeatedly subtract the divisor: Subtract the divisor (4) repeatedly from the dividend:
- 60 - 4 = 56
- 56 - 4 = 52
- 52 - 4 = 48
- 48 - 4 = 44
- 44 - 4 = 40
- 40 - 4 = 36
- 36 - 4 = 32
- 32 - 4 = 28
- 28 - 4 = 24
- 24 - 4 = 20
- 20 - 4 = 16
- 16 - 4 = 12
- 12 - 4 = 8
- 8 - 4 = 4
- 4 - 4 = 0
-
Count the subtractions: Count how many times you subtracted the divisor (4). You subtracted it 15 times.
-
The result: The number of times you subtracted the divisor is the quotient. Therefore, 60 divided by 4 is 15.
Method 3: Multiplication – The Inverse Operation
Division and multiplication are inverse operations. This means that if you multiply the quotient by the divisor, you should get the dividend. We can use this relationship to check our answer or even to solve the problem directly if we know the multiplication facts.
Since 4 x 15 = 60, we know that 60 divided by 4 is 15. This method relies on your knowledge of multiplication tables, making it a quick and efficient approach for familiar numbers.
Method 4: Mental Math Techniques – Building Number Sense
With practice, you can solve 60 ÷ 4 mentally using various techniques. Here are a couple of approaches:
-
Breaking down the numbers: Think of 60 as 40 + 20. 40 divided by 4 is 10, and 20 divided by 4 is 5. Adding 10 and 5 gives you 15.
-
Using known facts: You might know that 4 x 10 = 40, and 4 x 5 = 20. Since 40 + 20 = 60, you can deduce that 4 x 15 = 60, therefore 60 ÷ 4 = 15.
Real-World Applications of Division: Beyond the Classroom
Division is not just a theoretical concept; it's a practical tool used extensively in everyday life. Here are some examples:
-
Sharing equally: If you have 60 candies to share equally among 4 friends, each friend receives 15 candies.
-
Calculating unit price: If a pack of 4 shirts costs $60, each shirt costs $15.
-
Portioning ingredients: A recipe requires 60 grams of flour to be divided into 4 equal portions. Each portion will use 15 grams of flour.
-
Averaging data: If you have 4 test scores totaling 60 points, your average score is 15 points.
-
Understanding rates: If a car travels 60 kilometers in 4 hours, its average speed is 15 kilometers per hour.
The Mathematical Concept of Divisibility
The fact that 60 is evenly divisible by 4 (meaning there is no remainder) relates to the concept of divisibility rules. A number is divisible by 4 if its last two digits are divisible by 4. In this case, the last two digits of 60 are 60, and 60 is divisible by 4 (60 ÷ 4 = 15). This rule simplifies the process of determining divisibility without performing the actual division.
Frequently Asked Questions (FAQ)
-
What if I have a remainder? If the division doesn't result in a whole number, you'll have a remainder. For example, if you divide 61 by 4, you get 15 with a remainder of 1. This can be expressed as 15 R1 (15 remainder 1) or as a decimal (15.25).
-
How can I improve my division skills? Practice is key! Work through various division problems, starting with simpler ones and gradually increasing the complexity. Use different methods to build a deeper understanding.
-
Are there online resources to help me with division? Yes, many websites and apps offer interactive exercises and tutorials on division.
-
What if the divisor is larger than the dividend? If the divisor is larger than the dividend, the quotient will be less than 1 (a fraction or decimal). For instance, 4 ÷ 60 is approximately 0.0667.
Conclusion: Mastering Division – A Building Block for Mathematical Success
Understanding division, even a seemingly simple problem like 60 divided by 4, is crucial for building a strong mathematical foundation. This article explored multiple approaches to solving this problem, emphasizing the importance of understanding the underlying principles rather than just memorizing the answer. From long division to mental math techniques, and from recognizing the inverse relationship with multiplication to appreciating real-world applications, we've seen the versatility and practical significance of this fundamental operation. By mastering division, you unlock the door to more complex mathematical concepts and problem-solving skills, empowering you to tackle a wider range of challenges both in the classroom and in everyday life. Remember, consistent practice and exploring different methods are key to building confidence and fluency in division.
Latest Posts
Latest Posts
-
10 Of 34
Sep 23, 2025
-
Asap Rockys Hair
Sep 23, 2025
-
Bias Media Chart
Sep 23, 2025
-
3 8 Of 400
Sep 23, 2025
-
7 Of 1500
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 60divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.