72 Divided 6
interactiveleap
Sep 24, 2025 · 5 min read
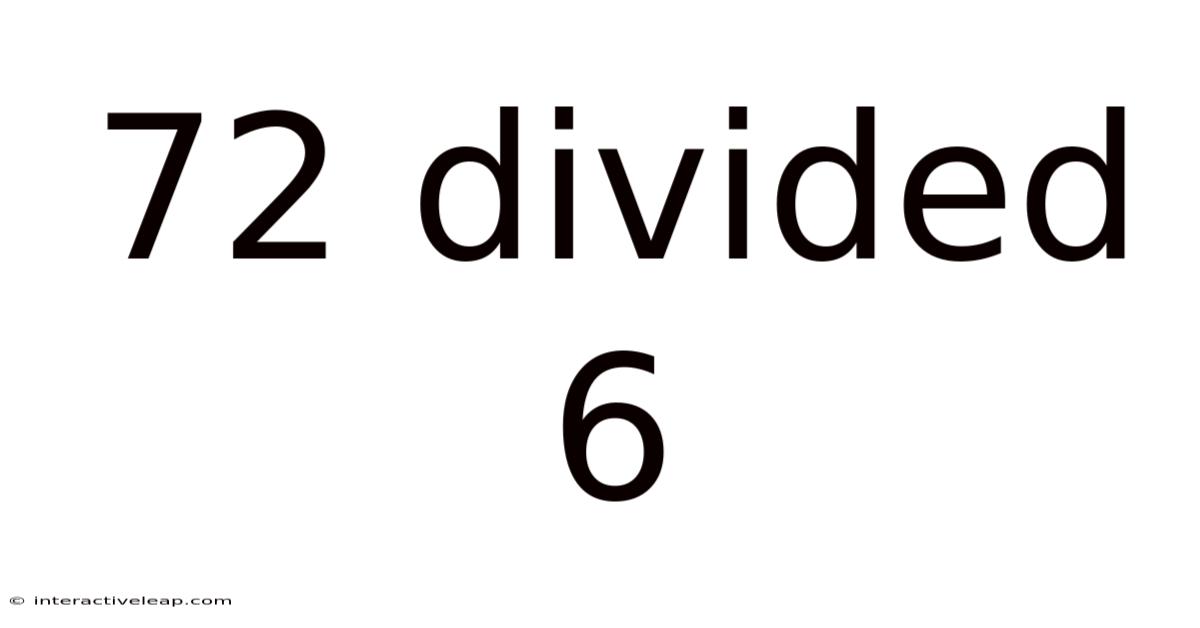
Table of Contents
Unpacking 72 Divided by 6: A Deep Dive into Division
Introduction: This article explores the seemingly simple mathematical problem of 72 divided by 6 (72 ÷ 6), delving far beyond the basic answer. We'll dissect the various methods for solving this problem, explore the underlying mathematical principles, examine real-world applications, and even touch upon the historical context of division. Understanding this seemingly simple equation provides a strong foundation for more complex mathematical concepts.
Understanding Division:
Before diving into the specifics of 72 ÷ 6, let's establish a fundamental understanding of division itself. Division is one of the four basic arithmetic operations (along with addition, subtraction, and multiplication). It essentially involves splitting a quantity into equal parts or groups. In the equation a ÷ b = c, 'a' is the dividend (the number being divided), 'b' is the divisor (the number you're dividing by), and 'c' is the quotient (the result). In our case, 72 is the dividend, 6 is the divisor, and we're looking for the quotient.
Methods for Solving 72 ÷ 6:
There are several ways to solve 72 ÷ 6, catering to different levels of mathematical understanding and preference:
-
Long Division: This traditional method is a systematic approach that works for any division problem. It involves a series of steps:
- Set up: Write the dividend (72) inside the long division symbol and the divisor (6) outside.
- Divide: Determine how many times the divisor (6) goes into the first digit of the dividend (7). It goes in once (1). Write the '1' above the 7.
- Multiply: Multiply the quotient digit (1) by the divisor (6), resulting in 6. Write this below the 7.
- Subtract: Subtract the result (6) from the first digit of the dividend (7), resulting in 1.
- Bring down: Bring down the next digit of the dividend (2), placing it next to the 1, making it 12.
- Repeat: Determine how many times the divisor (6) goes into 12. It goes in twice (2). Write the '2' above the 2.
- Multiply & Subtract: Multiply the quotient digit (2) by the divisor (6) (resulting in 12) and subtract it from 12, resulting in 0.
- Result: The quotient is 12.
-
Multiplication: Since division is the inverse of multiplication, you can solve 72 ÷ 6 by asking, "What number multiplied by 6 equals 72?" If you know your multiplication tables, you'll quickly recall that 6 x 12 = 72. Therefore, 72 ÷ 6 = 12.
-
Repeated Subtraction: This method involves repeatedly subtracting the divisor from the dividend until you reach zero. Each subtraction represents one group. Subtracting 6 from 72 twelve times results in zero, indicating that there are 12 groups of 6 in 72.
-
Using a Calculator: For larger or more complex division problems, a calculator provides a quick and efficient solution. Simply input 72 ÷ 6 and press the equals button to get the answer: 12.
Real-World Applications:
The concept of dividing 72 by 6, while seemingly abstract, has numerous real-world applications:
-
Sharing Equally: Imagine you have 72 candies to distribute equally among 6 friends. Dividing 72 by 6 tells you that each friend receives 12 candies.
-
Pricing: If 6 identical items cost $72, dividing 72 by 6 gives you the price of a single item ($12).
-
Measurement: If a 72-inch long piece of wood needs to be divided into 6 equal sections, each section will be 12 inches long.
-
Time Management: If a task takes 72 minutes and you want to break it into 6 equal sessions, each session will last 12 minutes.
-
Recipe Scaling: If a recipe calls for 72 grams of flour for 6 servings and you want to make only one serving, you would divide 72 by 6 to find the amount of flour needed (12 grams).
The Importance of Understanding the Process:
While a calculator can quickly provide the answer (12), it's crucial to understand the process of division. This understanding allows for problem-solving in situations where a calculator isn't readily available or where a deeper understanding of the quantities is required. It builds a strong foundation for more advanced mathematical concepts, including fractions, decimals, and algebra.
Exploring Related Concepts:
Understanding 72 ÷ 6 opens doors to exploring related mathematical concepts:
-
Factors and Multiples: The numbers 6 and 12 are factors of 72, meaning they divide evenly into 72. 72 is a multiple of both 6 and 12.
-
Prime Factorization: Breaking down 72 into its prime factors (2 x 2 x 2 x 3 x 3) helps to understand its divisibility by 6 (2 x 3).
-
Fractions: The problem can be represented as the fraction 72/6, which simplifies to 12/1 or simply 12.
-
Decimals: If the dividend wasn't perfectly divisible by the divisor, the result would be a decimal. For example, 73 ÷ 6 would result in a decimal answer.
Frequently Asked Questions (FAQ):
-
What is the remainder if you divide 73 by 6? When you perform long division, you find that 6 goes into 73 twelve times with a remainder of 1.
-
How can I check my answer? Multiply the quotient (12) by the divisor (6). If the result is the dividend (72), your answer is correct.
-
Are there other ways to solve division problems? Yes, different methods exist depending on the complexity of the problem, including using reciprocals (in algebra) or specialized algorithms for very large numbers.
-
Why is division important? Division is a fundamental operation in mathematics with wide applications in everyday life, from simple tasks to complex scientific calculations.
-
What if the divisor is zero? Dividing by zero is undefined in mathematics. It's an operation that has no meaningful result.
Conclusion:
The seemingly simple problem of 72 divided by 6 provides a rich opportunity to explore fundamental mathematical concepts and their real-world applications. While the answer is straightforward (12), the understanding of the underlying principles, the various methods of solving the problem, and the connections to other mathematical concepts are invaluable. Mastering this fundamental concept lays a crucial foundation for success in more advanced mathematical endeavors. By understanding the "why" behind the "what," we gain a deeper appreciation for the power and elegance of mathematics. Remember, the journey of understanding is often more rewarding than the destination itself.
Latest Posts
Latest Posts
-
28 Times 3
Sep 24, 2025
-
Twist Hair Bun
Sep 24, 2025
-
0 14 In Fraction
Sep 24, 2025
-
10 Of 27000
Sep 24, 2025
-
150kph In Mph
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 72 Divided 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.