28 Times 3
interactiveleap
Sep 24, 2025 · 5 min read
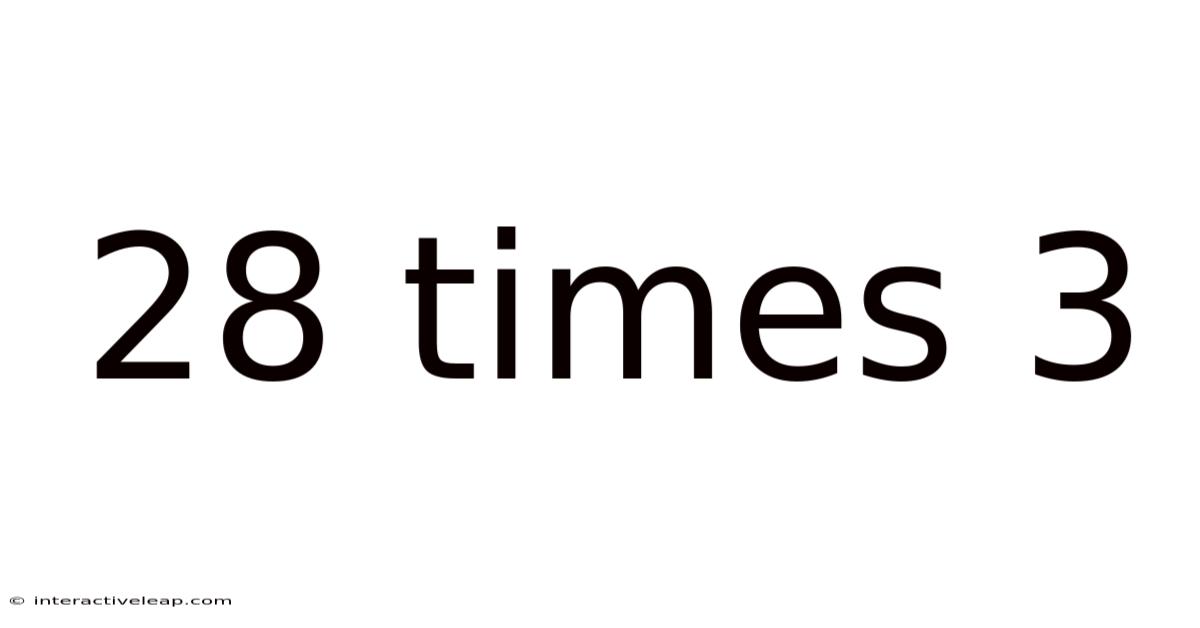
Table of Contents
Decoding 28 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple calculation of 28 multiplied by 3, delving far beyond the immediate answer to uncover the underlying mathematical principles and real-world applications. We'll unpack the process, examine different methods for solving the problem, and explore the broader context of multiplication in various fields. This comprehensive guide is designed for learners of all levels, from elementary school students grasping the fundamentals to those seeking a deeper understanding of mathematical operations. We'll also address common questions and misconceptions surrounding multiplication.
Understanding the Problem: 28 x 3
At its core, 28 x 3 represents a repeated addition problem. It asks: what is the total when you add 28 to itself three times? This simple interpretation forms the foundation for understanding multiplication. We can represent this visually:
28 + 28 + 28 = ?
While this approach is effective for smaller numbers, it becomes cumbersome for larger values. Multiplication provides a concise and efficient method for handling such calculations.
Methods for Solving 28 x 3
Several methods can be used to solve 28 x 3. Let's explore the most common approaches:
1. Standard Multiplication Algorithm
This is the method most commonly taught in schools. It involves multiplying the units digit first, then the tens digit, and finally adding the partial products:
28
x 3
----
24 (3 x 8)
+60 (3 x 20)
----
84
This method breaks down the multiplication into simpler steps, making it manageable even for larger numbers. It emphasizes place value, highlighting the importance of the position of each digit in determining its value.
2. Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can apply this to solve 28 x 3:
28 x 3 = (20 + 8) x 3 = (20 x 3) + (8 x 3) = 60 + 24 = 84
This method showcases the underlying mathematical principles and highlights the relationship between addition and multiplication. It provides a flexible approach, particularly useful when dealing with more complex numbers.
3. Lattice Multiplication
Lattice multiplication is a visual method that can be helpful for understanding the process and for larger multiplications. It involves creating a grid and breaking down the numbers into their place values.
2 | 8
-------
3 | 6 | 2 | 4
-------
8 | 4
The diagonal lines help organize the partial products, making it easier to add them up to obtain the final result (84). This method is particularly effective for larger numbers as it minimizes the risk of errors in carrying over digits.
4. Mental Math Techniques
With practice, you can develop mental math skills to solve this quickly. One technique is to double and add:
- Double 28: 56
- Add 28 to 56: 84
This method leverages your knowledge of doubling and addition to arrive at the answer efficiently. Other mental math strategies might involve breaking down the numbers into easier-to-manage parts. For example, you could think of 28 as 30 - 2, then calculate 3 x 30 = 90 and subtract 3 x 2 = 6, resulting in 90 - 6 = 84.
The Significance of Multiplication: Beyond the Numbers
The seemingly simple calculation of 28 x 3 has broader implications within mathematics and numerous real-world applications.
1. Foundational Arithmetic Operation
Multiplication is a fundamental arithmetic operation, forming the basis for more complex calculations in algebra, calculus, and other advanced mathematical fields. It’s the cornerstone of many problem-solving techniques and is crucial for understanding ratios, proportions, and percentages.
2. Real-World Applications:
Multiplication is ubiquitous in everyday life. Consider these examples:
- Shopping: Calculating the total cost of multiple items (e.g., 3 shirts at $28 each).
- Cooking: Adjusting recipes (e.g., tripling a recipe that calls for 28 grams of flour).
- Construction: Determining material needs (e.g., calculating the number of bricks required for a wall).
- Finance: Calculating interest or total earnings (e.g., calculating the total interest earned on an investment over 3 years).
- Science: Solving problems involving rates, ratios, and proportions in physics, chemistry, and biology.
In each of these scenarios, understanding multiplication is essential for accurate and efficient problem-solving.
Addressing Common Questions and Misconceptions
Several common misconceptions surround multiplication:
- Order of operations: While multiplication is commutative (28 x 3 = 3 x 28), it's crucial to follow the correct order of operations (PEMDAS/BODMAS) when dealing with more complex equations involving other operations like addition, subtraction, division, exponents, and parentheses.
- Multiplication as repeated addition: While helpful for understanding the concept, this definition is limited when dealing with fractions or decimals.
- Memorization vs. understanding: While memorizing multiplication tables is beneficial, a deeper understanding of the underlying principles is crucial for applying multiplication to diverse problem-solving contexts.
Conclusion: Mastering Multiplication
Mastering multiplication goes beyond simply knowing the answer to 28 x 3. It involves understanding the underlying principles, exploring different methods for solving problems, and appreciating its broad applicability in various fields. By developing a strong foundation in multiplication, you build a solid base for more advanced mathematical concepts and equip yourself with a valuable skill applicable to numerous real-world situations. The ability to quickly and accurately perform multiplication simplifies everyday tasks and enhances problem-solving capabilities across diverse disciplines. From balancing your budget to designing a building, the power of multiplication is undeniable. Continue practicing, explore different techniques, and embrace the fascinating world of mathematics. The journey to mastering multiplication is a journey to mastering a crucial tool for understanding and interacting with the world around us.
Further Exploration: Extending the Concept
This exploration of 28 x 3 can serve as a springboard for further learning. Consider exploring:
- Multiplication with larger numbers: Practice multiplying larger numbers using the various methods described above.
- Multiplication with decimals and fractions: Extend your understanding to include multiplication involving decimal numbers and fractions.
- Advanced mathematical concepts: Explore how multiplication forms the foundation for more advanced concepts in algebra, calculus, and other branches of mathematics.
- Real-world applications: Identify and analyze how multiplication is used in your daily life and in various professions.
By consistently practicing and exploring these areas, you'll not only solidify your understanding of multiplication but also unlock a deeper appreciation for the power and versatility of this fundamental mathematical operation. The journey of mathematical exploration is a continuous process of learning, discovery, and application – and it all starts with understanding the fundamentals, like 28 x 3.
Latest Posts
Latest Posts
-
0 83 In Fraction
Sep 24, 2025
-
Comparative Advantage Example
Sep 24, 2025
-
85 Of 130
Sep 24, 2025
-
25 Of 47
Sep 24, 2025
-
Symbols Of Courage
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 28 Times 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.