70 Of 38
interactiveleap
Sep 23, 2025 · 5 min read
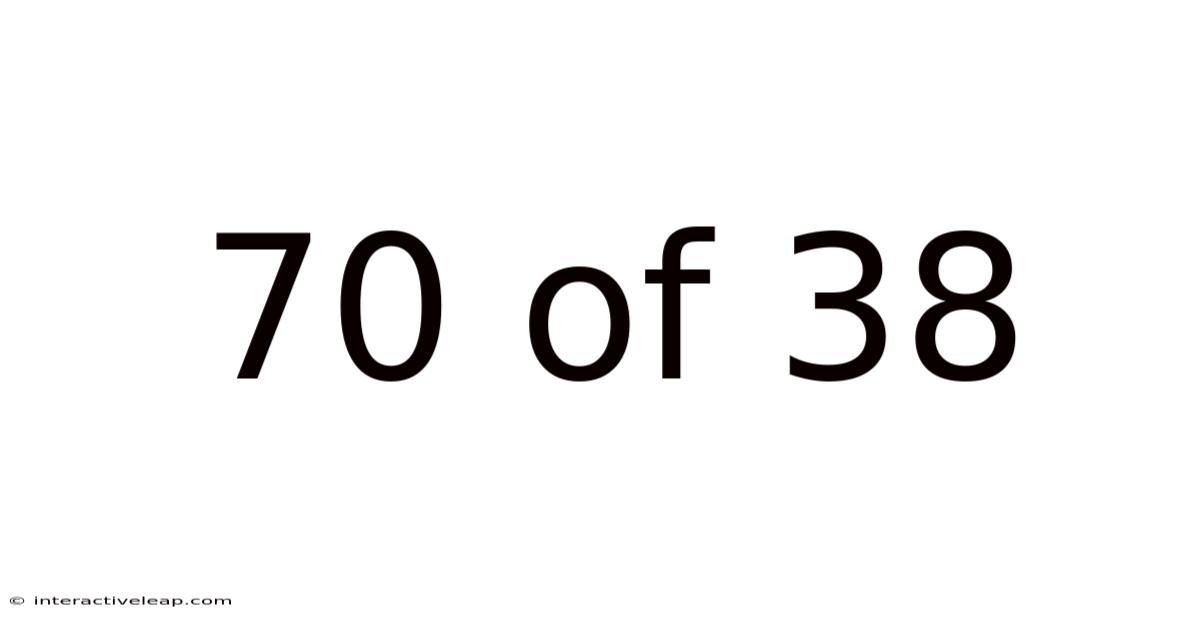
Table of Contents
Decoding 70 out of 38: Understanding Ratios, Percentages, and Their Applications
This article delves into the seemingly contradictory statement, "70 out of 38," exploring the mathematical concepts behind it, its practical interpretations, and common scenarios where such a ratio might arise. We'll unpack the meaning, discuss potential errors, and examine how to properly represent and interpret this type of data. Understanding ratios and percentages is crucial in various fields, from finance and statistics to everyday life decision-making.
Introduction: The Paradox of "70 out of 38"
At first glance, the phrase "70 out of 38" seems illogical. How can you have 70 items when you only started with 38? This apparent paradox highlights a crucial point: the numbers in a ratio don't always represent a simple count of objects. The context is vital. "70 out of 38" could represent a number of things, including an incorrect count, a projected value, a ratio of change, or even a misunderstanding of the data. Let's explore these possibilities.
Scenario 1: Incorrect Data Entry or Measurement Error
The most straightforward explanation is a simple mistake. Perhaps there was an error in data entry, a miscalculation, or an inaccurate measurement. Someone might have mistakenly recorded 70 instead of a more reasonable number, perhaps closer to 38, or vice versa. This scenario emphasizes the importance of double-checking data and ensuring accuracy in any measurement or recording process. Human error is a significant source of inconsistencies in data analysis.
Scenario 2: Projected Values or Extrapolation
"70 out of 38" could represent a projected value. Imagine a scenario where 38 units were sold in the first week of a product launch, and based on various market analyses and trends, the projected sales for the next week is 70 units. The ratio doesn't refer to existing units; it projects a future outcome. This is common in business forecasting, sales projections, and population growth estimations. Extrapolation techniques, while useful, inherently carry uncertainty.
Scenario 3: Ratios Representing Change or Growth
The numbers might not represent absolute quantities but rather a relative change or growth. For example, imagine a company's stock price increased from 38 points to 70 points. The ratio "70 out of 38" could then represent the proportional increase in stock value. In this case, it's not about the raw numbers, but the percentage change, calculated as [(70-38)/38] * 100% ≈ 84.2%. Understanding percentage change is essential for interpreting financial data and growth metrics.
Scenario 4: Misinterpretation of Data Categories
The phrase might reflect a misinterpretation of different categories. Consider a survey with 38 respondents in one group and 70 in another, unrelated group. The ratio "70 out of 38" is meaningless in this context because the groups are distinct and cannot be compared directly. Proper data categorization and analysis are essential to avoid spurious correlations and misleading interpretations.
Understanding Ratios and Percentages: A Mathematical Perspective
A ratio is a comparison of two numbers. In the case of "70 out of 38," the ratio is 70:38, which can be simplified to approximately 1.84:1. This means that for every one unit of the second quantity, there are approximately 1.84 units of the first. However, as we've discussed, the context matters greatly.
A percentage is a way of expressing a ratio as a fraction of 100. To calculate the percentage in our example, we would usually divide 70 by 38 and multiply by 100:
(70/38) * 100% ≈ 184.2%
This 184.2% figure, however, should be interpreted cautiously, given the potential for errors or misunderstandings discussed above. If this represents a percentage increase, the interpretation is clear. But if it is based on incorrect data, the resulting percentage is meaningless.
Step-by-Step Guide to Analyzing Ratios and Percentages
To accurately analyze a ratio like "70 out of 38," follow these steps:
-
Clarify the Context: Understand what the numbers represent. What is being measured or counted? Are they absolute values, projections, or changes over time?
-
Check for Errors: Examine the data source for potential errors in recording, measurement, or calculation. Are the numbers plausible given the context?
-
Calculate the Ratio: Express the relationship between the two numbers as a ratio (70:38 in our example). Simplify the ratio if possible.
-
Calculate the Percentage: Convert the ratio to a percentage by dividing the first number by the second and multiplying by 100.
-
Interpret the Result: Consider the context and potential sources of error when interpreting the percentage. What does this percentage tell you about the relationship between the two quantities?
Practical Applications in Different Fields
The concepts of ratios and percentages are widely used across various fields:
- Finance: Calculating returns on investment (ROI), comparing stock prices, analyzing financial statements.
- Statistics: Representing proportions in datasets, calculating probabilities, performing statistical analysis.
- Business: Analyzing sales figures, market share, customer demographics, and performance metrics.
- Science: Expressing experimental results, calculating concentrations, and reporting scientific data.
- Everyday Life: Calculating tips, discounts, proportions in cooking recipes, and comparing prices.
Frequently Asked Questions (FAQs)
-
Q: Can a percentage be greater than 100%? A: Yes, a percentage can be greater than 100% if it represents a change or growth relative to an initial value. For example, a 150% increase signifies that the final value is 1.5 times the initial value.
-
Q: How do I identify data errors in a ratio? A: Look for inconsistencies in the data, unrealistic values, or values that don't align with known trends or expectations. Cross-reference the data with other sources to verify accuracy.
-
Q: What are some common mistakes when working with ratios and percentages? A: Common mistakes include incorrect calculations, misinterpreting the context, and neglecting units of measurement. Double-checking calculations and understanding the meaning of the numbers is crucial.
Conclusion: The Importance of Context and Accuracy
The phrase "70 out of 38" highlights the importance of critically examining data and understanding the context. While the raw numbers may seem paradoxical, the underlying mathematical concepts of ratios and percentages are fundamental tools for analyzing data across numerous disciplines. By following a systematic approach to analyzing ratios and percentages, and by being mindful of potential errors, we can ensure accurate and meaningful interpretations of data, leading to better decision-making and a deeper understanding of the world around us. Remember that context is key, and always double-check your data sources for accuracy. A seemingly contradictory ratio often signifies the need for further investigation and clarification.
Latest Posts
Latest Posts
-
78 1kg To Lbs
Sep 23, 2025
-
12 Of 750
Sep 23, 2025
-
794mm In Cm
Sep 23, 2025
-
14oz To Ml
Sep 23, 2025
-
2000m In Ft
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 70 Of 38 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.