12 Of 750
interactiveleap
Sep 23, 2025 · 5 min read
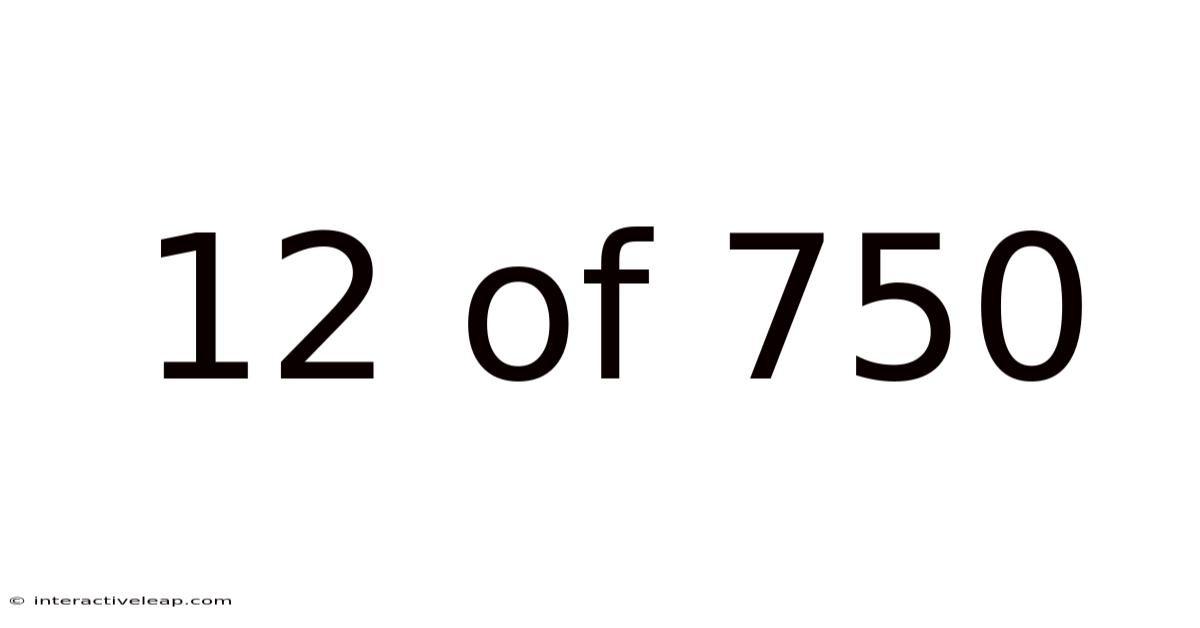
Table of Contents
Decoding the Enigma: Understanding the Fraction 12/750 and its Implications
The seemingly simple fraction 12/750 might appear insignificant at first glance. However, understanding its implications requires delving into the world of fractions, simplification, decimals, percentages, and even their real-world applications. This article will guide you through a comprehensive exploration of 12/750, uncovering its hidden depths and demonstrating its relevance in various contexts. We'll move beyond a simple calculation and explore the underlying mathematical principles, providing you with a strong foundational understanding.
Introduction: The Power of Fractions
Fractions, at their core, represent parts of a whole. They're a fundamental building block in mathematics, used extensively in various fields, from cooking and construction to finance and scientific research. Understanding fractions, including their simplification, conversion to decimals and percentages, is crucial for effective problem-solving and critical thinking. The fraction 12/750, although seemingly small, serves as an excellent example to illustrate these core concepts.
1. Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before we delve into further calculations, simplifying the fraction is paramount. This involves finding the greatest common divisor (GCD) of the numerator (12) and the denominator (750). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To find the GCD of 12 and 750, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- 12: 2 x 2 x 3
- 750: 2 x 3 x 5 x 5 x 5
The common prime factors are 2 and 3. Therefore, the GCD is 2 x 3 = 6.
Now, we divide both the numerator and the denominator by the GCD:
12 ÷ 6 = 2 750 ÷ 6 = 125
This simplifies the fraction 12/750 to its simplest form: 2/125. This simplified fraction is much easier to work with in subsequent calculations and provides a clearer understanding of the relative proportion.
2. Converting the Fraction to a Decimal: Understanding the Proportion
Converting the simplified fraction 2/125 to a decimal provides a different perspective on its value. To do this, we divide the numerator (2) by the denominator (125):
2 ÷ 125 = 0.016
Therefore, the decimal equivalent of 12/750 (or its simplified form 2/125) is 0.016. This decimal representation clearly shows that the fraction represents a small proportion of the whole.
3. Expressing the Fraction as a Percentage: Visualizing the Proportion
Percentages provide another way to visualize the proportion represented by the fraction. To convert the decimal 0.016 to a percentage, we multiply it by 100:
0.016 x 100 = 1.6%
Therefore, 12/750 represents 1.6% of the whole. This percentage representation is particularly useful for comparing proportions and making relative judgments.
4. Real-World Applications: Contextualizing the Fraction
The fraction 12/750, and its simplified and converted forms, can be applied in numerous real-world scenarios. Consider these examples:
-
Survey Results: If 12 out of 750 respondents chose a particular option in a survey, the fraction 12/750 represents the proportion of respondents who selected that option. The percentage (1.6%) provides a concise and easily understandable summary of the results.
-
Manufacturing Defects: If 12 out of 750 manufactured items are defective, the fraction indicates the defect rate. The simplified fraction and percentage highlight the level of quality control needed.
-
Financial Investments: Imagine an investment of $750 yielding a return of $12. The fraction 12/750 represents the return on investment (ROI), which can then be converted into a percentage to assess the profitability of the investment.
-
Scientific Experiments: In scientific experiments, ratios and proportions are frequently used. The fraction 12/750 could represent the ratio of a specific substance in a larger sample, aiding in analysis and understanding.
5. Mathematical Operations with the Fraction:
Understanding the fraction 12/750 also allows us to perform various mathematical operations. For example:
-
Addition/Subtraction: If we need to add or subtract this fraction from other fractions, simplifying it to 2/125 makes the calculation much easier.
-
Multiplication/Division: Multiplying or dividing the fraction by other numbers also becomes simpler after simplification. For instance, multiplying 2/125 by 5 results in 10/125, which can be further simplified.
-
Working with mixed numbers: If this fraction were part of a calculation involving mixed numbers (a whole number and a fraction), simplifying the fraction would make the process more manageable.
6. Further Exploration: Expanding on the Concepts
The exploration of 12/750 extends beyond basic calculations. It opens doors to more advanced mathematical concepts:
-
Ratios and Proportions: Fractions are the cornerstone of understanding ratios and proportions. The ratio 12:750, simplified to 2:125, indicates a relationship between two quantities.
-
Probability: The fraction can represent a probability. If there are 750 possible outcomes and 12 favorable outcomes, the probability of a favorable outcome is 12/750, or 1.6%.
-
Algebra: Fractions are essential in algebraic equations. Solving for an unknown variable might involve manipulating fractions similar to 12/750.
7. Frequently Asked Questions (FAQ)
-
Q: Can I simplify 12/750 any further than 2/125?
- A: No. 2 and 125 share no common factors other than 1, meaning 2/125 is the simplest form.
-
Q: What is the difference between a fraction, a decimal, and a percentage?
- A: They are different ways of representing the same proportion. A fraction uses a numerator and denominator, a decimal uses a base-10 system, and a percentage expresses the proportion as parts per hundred.
-
Q: Why is simplifying a fraction important?
- A: Simplifying makes calculations easier, provides a clearer understanding of the proportion, and reduces the risk of errors.
-
Q: Are there other methods to find the GCD besides prime factorization?
- A: Yes, the Euclidean algorithm is another efficient method for finding the GCD.
8. Conclusion: The Significance of Understanding Fractions
The seemingly innocuous fraction 12/750 serves as a powerful illustration of fundamental mathematical concepts. By simplifying, converting to decimals and percentages, and exploring its real-world applications, we've gained a deeper understanding of its significance. The ability to work confidently with fractions is essential for success in various academic and professional endeavors. Remember, understanding the underlying principles allows you to tackle more complex mathematical problems with greater ease and confidence. Mastering fractions is not just about numbers; it's about developing a strong foundation for critical thinking and problem-solving skills that extend far beyond the classroom. The journey of understanding fractions, beginning with something as seemingly small as 12/750, can lead to a profound appreciation for the elegance and power of mathematics.
Latest Posts
Latest Posts
-
Motherboard And Components
Sep 24, 2025
-
Camisetas In English
Sep 24, 2025
-
Kilopascals To Atmospheres
Sep 24, 2025
-
70 Of 64
Sep 24, 2025
-
3 8 Of 72
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 12 Of 750 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.