7 X Pi
interactiveleap
Sep 19, 2025 · 6 min read
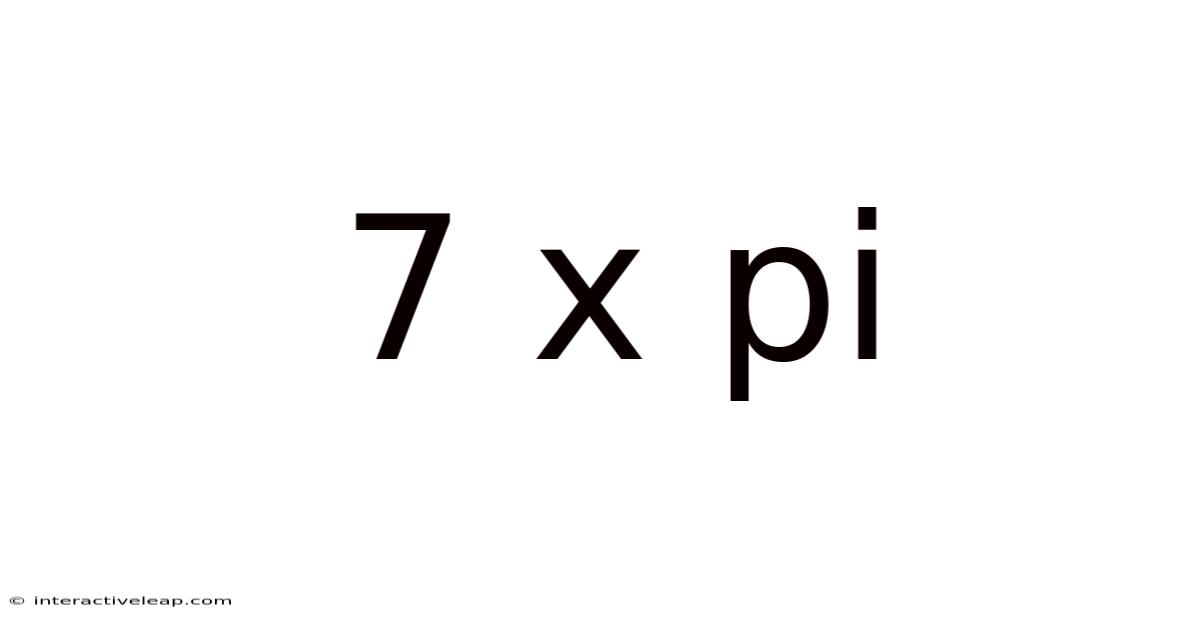
Table of Contents
Unveiling the Mysteries of 7π: Exploring a Mathematical Constant
The number π (pi), approximately 3.14159, is a fundamental constant in mathematics, representing the ratio of a circle's circumference to its diameter. While π itself is extensively studied and understood, its multiples, such as 7π, offer intriguing avenues for exploration within various mathematical fields. This article delves into the significance of 7π, exploring its properties, applications, and the broader context within which it resides. We'll uncover its relevance in geometry, trigonometry, calculus, and even physics, demonstrating that even seemingly simple multiples of π hold profound mathematical weight. Understanding 7π enhances our comprehension of π's pervasive influence across diverse branches of mathematics and science.
Understanding the Significance of π (Pi)
Before delving into the specifics of 7π, let's refresh our understanding of π. Pi is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation continues infinitely without repeating. Its value is approximately 3.14159265359... This seemingly simple constant is crucial in calculating the circumference and area of circles, the volume and surface area of spheres, and countless other geometric and trigonometric relationships. Its importance extends far beyond basic geometry; it appears unexpectedly in diverse fields like probability, statistics, and even quantum physics.
Calculating and Approximating 7π
Calculating 7π is straightforward: simply multiply the value of π by 7. Using a calculator or computer software with sufficient precision, we find that:
7π ≈ 21.9911485751...
While we can't express 7π exactly as a finite decimal or fraction, we can approximate it to any desired degree of accuracy. The approximation 21.9911 is often sufficient for many practical applications. However, for applications requiring higher precision, such as advanced calculations in engineering or physics, utilizing more decimal places is necessary. The precision needed depends entirely on the context of the calculation and the acceptable margin of error.
Geometric Applications of 7π
The most immediate applications of 7π are found in geometry. Imagine a circle with a radius of 7 units. The circumference of this circle is given by the formula C = 2πr, where 'r' is the radius. In our case, the circumference would be 14π. Now consider a situation where you need to calculate the circumference of a similar circle, but this time, you're dealing with a segment of the circle. This is where the relevance of 7π comes into play. Depending on the central angle subtended by the arc, a calculation might involve a multiple of π which can be simplified, potentially involving 7π. For instance, if dealing with a sector representing a significant portion of the circle.
Similarly, consider the area of a circle with radius 7/2. The area is given by the formula A = πr², which in this case would lead to a calculation involving (49/4)π, showcasing how multiples of π, including 7π, appear naturally in even relatively straightforward geometrical problems. These types of applications illustrate the importance of multiples of π in more complex geometric calculations involving sectors, segments, and combined shapes.
Trigonometric and Calculus Applications
The constant 7π also features prominently in trigonometric functions. Recall that trigonometric functions like sine, cosine, and tangent are periodic functions with a period of 2π. This means that their values repeat every 2π radians. Consequently, values involving 7π will have trigonometric equivalents within the standard range of 0 to 2π. Calculating these values often involves employing trigonometric identities and reducing the argument (angle) to a more manageable form.
In calculus, 7π appears in integrals and derivatives involving trigonometric and exponential functions. For example, integrating functions involving sin(7πx) or cos(7πx) would involve the constant 7π as a factor in the resulting antiderivative. The integration techniques employed, such as u-substitution or integration by parts, often lead to expressions containing multiples of π, including 7π. Similar applications arise when dealing with Fourier series and transforms, which extensively utilize trigonometric functions and their integrals.
7π in Physics and Engineering
The significance of π, and consequently its multiples like 7π, extends into physics and engineering. In physics, many formulas relating to waves, oscillations, and circular motion involve π. For example, the angular frequency (ω) of a simple harmonic oscillator is related to the period (T) by the equation ω = 2π/T. Situations involving complex harmonic motions or the superposition of waves might lead to calculations involving multiples of 2π, and consequently, multiples of π such as 7π.
In engineering, the calculation of stress, strain, and other mechanical properties of circular components frequently involves π. Design calculations for pipes, shafts, or gears often use formulas that incorporate π, and complex scenarios involving these components could easily result in calculations involving multiples of π, like 7π. Similar applications arise in electrical engineering when dealing with AC circuits, where the frequency and phase of the current are usually expressed using multiples of π.
Beyond the Basics: Advanced Applications of 7π
While the applications mentioned above highlight the common occurrences of 7π, its significance extends to more advanced mathematical concepts.
-
Complex Analysis: In complex analysis, 7π appears in the context of complex exponential functions and contour integrals. The behavior of complex functions around singularities or branch cuts often involves calculations involving multiples of π.
-
Number Theory: While not as direct as in geometry or trigonometry, 7π’s relationship with π allows for indirect applications in number theory. Investigations into the properties of π and its relationship to other mathematical constants indirectly inform our understanding of numbers and their properties.
-
Probability and Statistics: The normal distribution, a fundamental concept in probability and statistics, is defined using the exponential function and involves π in its formula. While 7π itself might not directly appear in the basic formula, its significance lies in its relationship to the wider context of calculations involving the normal distribution and related statistical applications.
Frequently Asked Questions (FAQ)
Q: Is 7π a rational or irrational number?
A: 7π is an irrational number. Since π is irrational (its decimal representation is non-terminating and non-repeating), multiplying it by a rational number (7) does not make it rational.
Q: What is the exact value of 7π?
A: There is no exact value of 7π that can be expressed as a finite decimal or fraction. Its decimal representation is infinite and non-repeating.
Q: How is 7π used in computer programming?
A: In programming, 7π is typically represented using a high-precision floating-point approximation of π multiplied by 7. The accuracy of the approximation depends on the data type and the programming language used. Libraries often provide highly accurate approximations of π to minimize computational error.
Q: Are there other multiples of π that are equally important?
A: Yes, other multiples of π, such as 2π, π/2, and π/4, are equally, or even more, important in various mathematical and scientific contexts. These multiples frequently appear in formulas related to periodicity, trigonometric functions, and circular motion.
Conclusion: The Enduring Relevance of 7π
7π, while seemingly a simple multiple of a well-known constant, showcases the profound implications of exploring even the most basic mathematical relationships. Its significance extends beyond simple geometric calculations, encompassing diverse areas of mathematics, science, and engineering. From trigonometric functions to complex analysis and even applications in physics and engineering, the appearance of 7π highlights the pervasive and multifaceted nature of π itself. Understanding 7π reinforces our appreciation for the fundamental role of π in our understanding of the world around us and provides a deeper insight into the interconnectedness of various mathematical fields. The exploration of such multiples encourages a broader and more nuanced comprehension of mathematical principles and their far-reaching applications.
Latest Posts
Latest Posts
-
25 Of 320
Sep 19, 2025
-
119 5kg In Stone
Sep 19, 2025
-
Standard Form Indices
Sep 19, 2025
-
500mg To Grams
Sep 19, 2025
-
300mm In Metres
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 7 X Pi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.