25 Of 320
interactiveleap
Sep 19, 2025 · 6 min read
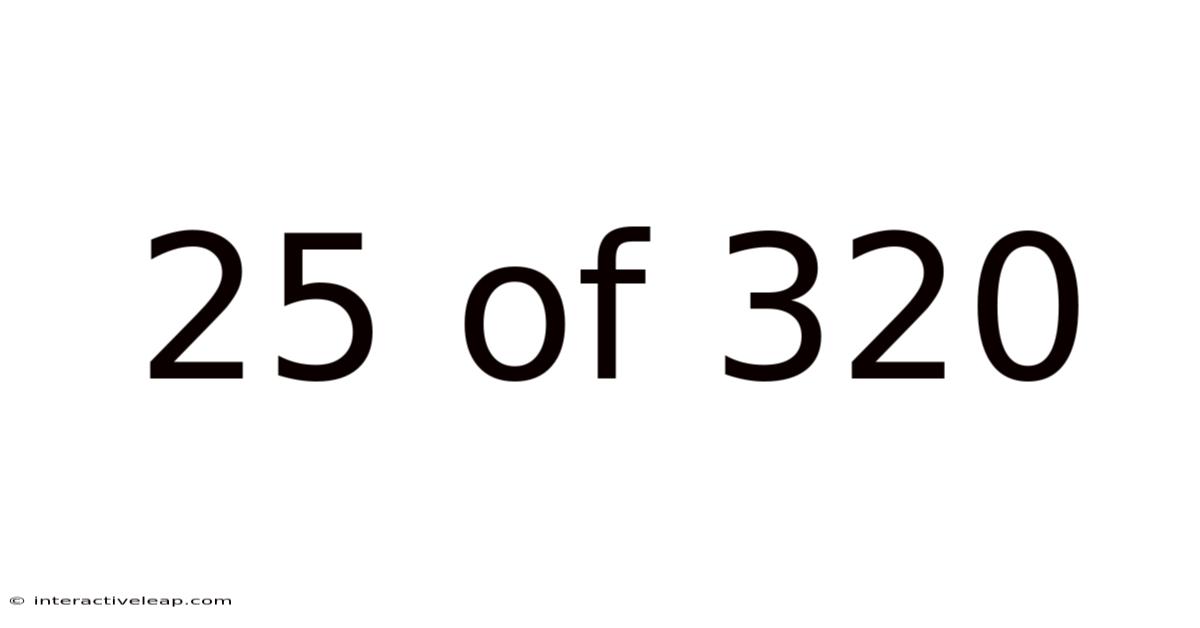
Table of Contents
Decoding the Fraction: Understanding the Significance of 25/320
The seemingly simple fraction 25/320 might appear insignificant at first glance. However, understanding its implications and exploring its various interpretations unveils a wealth of mathematical concepts and practical applications. This article will delve deep into the meaning of this fraction, exploring its simplification, decimal representation, percentage equivalence, and its relevance in different contexts. We will also touch upon related mathematical concepts to provide a comprehensive understanding. This exploration will be beneficial for students, educators, and anyone curious about the fascinating world of fractions and their practical uses.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
The first step in understanding 25/320 is to simplify it to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator (25) and the denominator (320). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
To find the GCD of 25 and 320, we can use the Euclidean algorithm. This algorithm involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
- Step 1: Divide 320 by 25. 320 ÷ 25 = 12 with a remainder of 20.
- Step 2: Divide 25 by 20. 25 ÷ 20 = 1 with a remainder of 5.
- Step 3: Divide 20 by 5. 20 ÷ 5 = 4 with a remainder of 0.
The last non-zero remainder is 5, therefore, the GCD of 25 and 320 is 5.
Now, we can simplify the fraction by dividing both the numerator and the denominator by the GCD:
25 ÷ 5 = 5 320 ÷ 5 = 64
Therefore, the simplified form of 25/320 is 5/64. This simplified fraction is easier to work with and represents the same value as the original fraction.
Converting to Decimal: Understanding the Decimal Representation
Converting a fraction to its decimal equivalent involves dividing the numerator by the denominator. In this case, we'll convert the simplified fraction 5/64 to its decimal form.
5 ÷ 64 ≈ 0.078125
Therefore, the decimal representation of 25/320 (or 5/64) is approximately 0.078125. This decimal representation is useful for various calculations and comparisons, particularly in contexts where decimal numbers are preferred.
Expressing as a Percentage: Interpreting the Fractional Value
To express the fraction as a percentage, we multiply the decimal representation by 100%.
0.078125 × 100% = 7.8125%
So, 25/320 is equivalent to 7.8125%. This percentage representation is useful for expressing the fraction as a proportion of a whole, often used in contexts like statistics, finance, and everyday life. For example, if 25 out of 320 students passed an exam, we can say that 7.8125% of the students passed.
Real-World Applications: Examples of 25/320 in Context
The fraction 25/320, or its simplified form 5/64, can represent various scenarios in real-world applications. Here are a few examples:
-
Test Scores: Imagine a test with 320 questions. If a student answered 25 questions correctly, their score would be 25/320, or 7.8125%. This percentage provides a clear understanding of their performance.
-
Survey Results: In a survey of 320 people, if 25 responded positively to a particular question, the positive response rate would be 7.8125%. This percentage helps analyze the overall sentiment or opinion.
-
Manufacturing Defects: In a batch of 320 manufactured items, if 25 were found to be defective, the defect rate would be 7.8125%. This percentage is crucial for quality control and process improvement.
-
Financial Investments: While less likely to encounter this precise fraction in financial contexts, the principle remains the same. This fraction could represent a small portion of an investment portfolio or a return on investment.
These examples illustrate the versatility of the fraction 25/320 and its applicability across various disciplines.
Exploring Related Mathematical Concepts
Understanding 25/320 also provides an opportunity to explore related mathematical concepts:
-
Ratio and Proportion: The fraction 25/320 represents a ratio of 25 to 320. This ratio can be used to compare two quantities. Understanding ratios and proportions is fundamental in many fields, including science, engineering, and economics.
-
Percentage Calculation: Converting the fraction to a percentage involves understanding the concept of percentages and their calculation. This skill is essential for everyday tasks, such as calculating discounts, interest rates, and tax rates.
-
Decimal Arithmetic: Working with the decimal equivalent of the fraction (0.078125) reinforces skills in decimal arithmetic, including addition, subtraction, multiplication, and division of decimal numbers.
-
Fraction Simplification: Simplifying the fraction to its lowest terms (5/64) highlights the importance of simplifying fractions for easier calculations and clearer understanding. This involves finding the greatest common divisor (GCD), a crucial concept in number theory.
-
Prime Factorization: Finding the prime factors of both 25 and 320 helps understand the composition of these numbers and facilitates the GCD calculation. 25 = 5 x 5 and 320 = 2 x 2 x 2 x 2 x 2 x 2 x 5. The common factor is 5.
Frequently Asked Questions (FAQ)
Q1: Can 25/320 be further simplified?
A1: Yes, as shown above, 25/320 simplifies to 5/64. This is the simplest form because the GCD of 5 and 64 is 1.
Q2: What is the reciprocal of 25/320?
A2: The reciprocal of a fraction is found by swapping the numerator and the denominator. The reciprocal of 25/320 is 320/25, which simplifies to 64/5 or 12.8.
Q3: How do I convert 25/320 to a percentage without using a calculator?
A3: While a calculator simplifies the process, you can convert it manually. First, simplify the fraction to 5/64. Then, divide 5 by 64 to get the decimal value, which can then be multiplied by 100 to obtain the percentage.
Q4: What are some real-world examples beyond those mentioned?
A4: The fraction could represent the proportion of a specific ingredient in a recipe, the success rate of a particular process, or the probability of an event occurring. The applications are vast and context-dependent.
Conclusion: The Broader Significance of Understanding Fractions
Understanding the fraction 25/320, though seemingly simple, opens the door to a deeper understanding of fundamental mathematical concepts. From simplifying fractions and calculating decimal and percentage equivalents to applying these skills in real-world scenarios, the journey of interpreting this fraction reinforces core mathematical skills. The exploration of related concepts like ratio, proportion, and prime factorization further broadens mathematical knowledge. The ability to confidently manipulate fractions is not just a mathematical skill but a crucial life skill applicable across various fields. Remember, every fraction, no matter how seemingly insignificant, holds a universe of mathematical possibilities waiting to be explored.
Latest Posts
Latest Posts
-
355ml In Oz
Sep 19, 2025
-
14 Of 700
Sep 19, 2025
-
94kgs In Stone
Sep 19, 2025
-
115lbs In Kg
Sep 19, 2025
-
Name Lacey Meaning
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 25 Of 320 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.