67 X 4
interactiveleap
Sep 15, 2025 · 6 min read
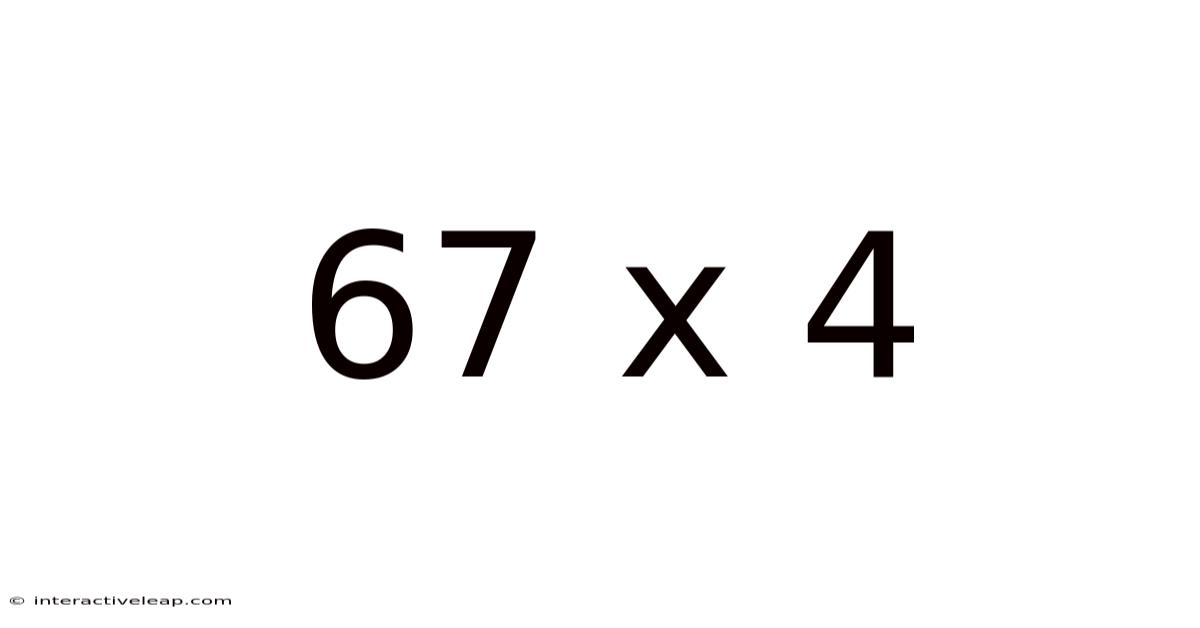
Table of Contents
Unlocking the Power of Multiplication: A Deep Dive into 67 x 4
This article explores the seemingly simple multiplication problem 67 x 4, transforming it into a gateway to understanding fundamental mathematical concepts and practical applications. We'll move beyond just finding the answer, delving into various methods of calculation, exploring the underlying principles, and uncovering the hidden connections to real-world scenarios. This comprehensive guide is suitable for students, educators, and anyone seeking to strengthen their mathematical skills and appreciation.
Introduction: More Than Just a Number
The equation 67 x 4 might seem trivial at first glance. However, this seemingly basic arithmetic problem provides a fertile ground for understanding core mathematical principles, including the commutative property, distributive property, and the importance of place value. By exploring different methods of solving this equation, we can appreciate the flexibility and elegance of mathematics. This exploration will not only help in calculating the answer but also in developing a deeper understanding of how numbers interact. We'll cover several methods – from the standard algorithm to more visual and intuitive approaches – ensuring a comprehensive understanding for learners of all levels.
Method 1: The Standard Algorithm
The standard multiplication algorithm is a widely taught method that involves breaking down the problem into smaller, manageable steps. Here's how to solve 67 x 4 using this method:
- Multiply the ones digit: 4 x 7 = 28. Write down the '8' and carry-over the '2'.
- Multiply the tens digit: 4 x 6 = 24. Add the carried-over '2': 24 + 2 = 26.
- Combine the results: The final answer is 268.
Therefore, 67 x 4 = 268. This method emphasizes place value, showing how multiplying the ones and tens digits separately and then combining the results correctly yields the final product.
Method 2: The Distributive Property
The distributive property of multiplication over addition states that a(b + c) = ab + ac. We can use this property to break down 67 x 4 into smaller, easier-to-manage calculations:
- Break down 67: We can rewrite 67 as 60 + 7.
- Apply the distributive property: 4 x (60 + 7) = (4 x 60) + (4 x 7)
- Calculate: (4 x 60) = 240 and (4 x 7) = 28
- Add the results: 240 + 28 = 268
This method demonstrates a fundamental algebraic concept, showing how complex calculations can be simplified by breaking them into smaller, more manageable parts. This approach strengthens conceptual understanding beyond procedural memorization.
Method 3: Repeated Addition
Multiplication can be visualized as repeated addition. 67 x 4 means adding 67 four times:
67 + 67 + 67 + 67 = 268
While this method might be less efficient for larger numbers, it provides a clear visual representation of what multiplication represents. This is particularly helpful for younger learners who are still grasping the concept of multiplication. It connects the abstract concept of multiplication to the concrete action of repeated addition.
Method 4: Using Arrays
Visual learners can benefit from representing the multiplication problem using an array. An array is a visual representation of multiplication using rows and columns. To represent 67 x 4, you would draw a rectangle with 67 rows and 4 columns. Each cell within the rectangle represents one unit, and the total number of cells represents the product.
While practically drawing a 67 x 4 array might be tedious, the concept remains useful for smaller numbers, helping to solidify the connection between multiplication and area. It emphasizes the spatial representation of multiplication and provides an alternative way to conceptualize the problem.
Method 5: Lattice Multiplication
Lattice multiplication, an ancient method, offers a structured and visual approach to multiplication. It’s particularly helpful for larger numbers and can be less prone to errors.
- Draw a lattice: Create a grid with two rows (for the tens and ones digits of 67) and one column for the multiplier (4).
- Multiply and place: Multiply each digit of 67 by 4 and place the result diagonally within the corresponding cell.
- Sum the diagonals: Add the numbers along each diagonal, carrying over any tens digit to the next diagonal.
This method provides a highly organized and visual way to handle multiplication, reducing the risk of calculation errors, especially with larger numbers.
Expanding the Understanding: Real-World Applications
The seemingly simple problem 67 x 4 has numerous practical applications in various real-world scenarios:
- Calculating Costs: Imagine buying 4 items that cost $67 each. The total cost would be 67 x 4 = $268.
- Measuring Distance: If you run 4 laps around a track that is 67 meters long, the total distance covered would be 268 meters.
- Problem Solving: Many word problems in mathematics, science, and even everyday life can be solved using multiplication. Understanding 67 x 4 provides a building block for more complex problem-solving skills.
- Area Calculation: If a rectangle has dimensions of 67 units by 4 units, its area would be 268 square units. This demonstrates the connection between multiplication and geometric concepts.
- Data Analysis: In data analysis, multiplication is frequently used in scaling data, performing calculations, and analyzing trends.
The Importance of Place Value
Understanding place value is crucial for mastering multiplication. In the number 67, the '6' represents 60 (6 tens) and the '7' represents 7 ones. When multiplying 67 by 4, we are essentially multiplying both the tens and ones place values separately and then combining the results: (4 x 60) + (4 x 7) = 240 + 28 = 268. This highlights the significance of understanding the positional value of each digit within a number.
Frequently Asked Questions (FAQ)
- What is the easiest way to calculate 67 x 4? The standard algorithm is generally considered the most efficient method for this particular problem. However, the best method depends on individual preferences and understanding.
- What are some common mistakes students make when solving this type of problem? Common mistakes include errors in carrying over digits, incorrect placement of digits in the final answer, and misunderstanding of place value.
- How can I improve my multiplication skills? Practice is key. Regular practice with various problems, using different methods, and focusing on understanding the underlying concepts will significantly improve multiplication skills.
- Can this be solved using a calculator? Yes, of course. Calculators are a valuable tool for checking answers and solving complex problems quickly, but it’s crucial to also understand the underlying mathematical principles.
Conclusion: Beyond the Answer
This in-depth exploration of 67 x 4 has demonstrated that even a seemingly simple multiplication problem can be a gateway to a deeper understanding of mathematics. By examining various calculation methods, exploring the underlying principles, and connecting the equation to real-world applications, we’ve moved beyond simply finding the answer (268) to appreciating the elegance and practicality of mathematical concepts. This understanding lays a solid foundation for tackling more complex mathematical challenges in the future and underscores the importance of developing strong mathematical reasoning skills. Mastering multiplication is not just about memorizing facts; it's about understanding the underlying principles and their diverse applications in various contexts. The journey of understanding 67 x 4 serves as a powerful illustration of this concept.
Latest Posts
Latest Posts
-
24 X 6
Sep 15, 2025
-
20 Of 14000
Sep 15, 2025
-
300 Of 5
Sep 15, 2025
-
7 8km In Miles
Sep 15, 2025
-
Laser Measure Tape
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 67 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.