24 X 6
interactiveleap
Sep 15, 2025 · 6 min read
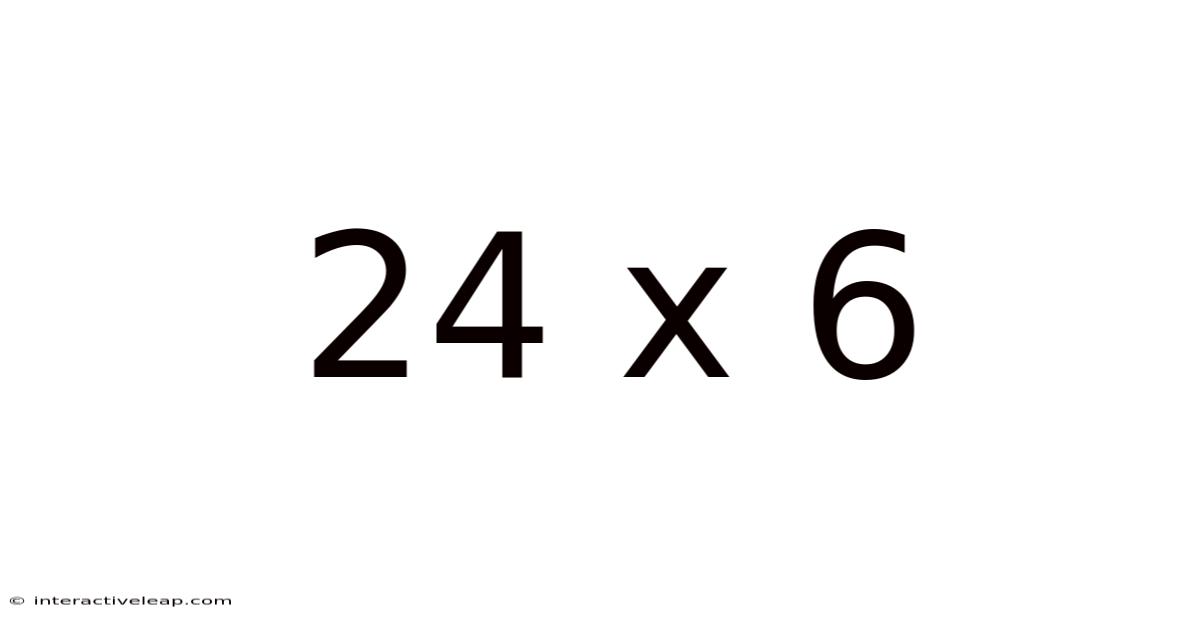
Table of Contents
Decoding 24 x 6: Exploring Multiplication, Area, and Beyond
The seemingly simple equation, 24 x 6, opens a door to a world of mathematical concepts. It's more than just a multiplication problem; it's a gateway to understanding area calculations, different multiplication strategies, and even the foundations of algebra. This article delves deep into the meaning of 24 x 6, exploring its various interpretations and applications, catering to learners of all levels.
Understanding the Fundamentals: What Does 24 x 6 Mean?
At its core, 24 x 6 represents repeated addition. It means adding 24 to itself six times: 24 + 24 + 24 + 24 + 24 + 24. The answer, 144, is the product of this multiplication. Understanding this basic concept is crucial before exploring more advanced applications. This seemingly simple equation forms the basis for many more complex calculations in mathematics and beyond.
Methods for Solving 24 x 6: A Multifaceted Approach
There are several ways to solve 24 x 6, each offering different insights into the nature of multiplication:
1. Traditional Multiplication:
This involves the standard long multiplication method taught in schools. This method involves multiplying the units digit of 24 (4) by 6, then the tens digit (2) by 6, and finally adding the results.
- 6 x 4 = 24 (Write down 4, carry-over 2)
- 6 x 2 = 12 + 2 (carry-over) = 14
- Therefore, 24 x 6 = 144
This method emphasizes place value and the distributive property of multiplication.
2. Distributive Property:
The distributive property states that a(b + c) = ab + ac. We can break down 24 into smaller, easier-to-manage numbers:
- 24 can be broken down into 20 + 4
- So, 24 x 6 = (20 + 4) x 6 = (20 x 6) + (4 x 6) = 120 + 24 = 144
This method is excellent for building number sense and understanding the underlying principles of multiplication.
3. Doubling and Halving:
This method leverages the commutative property of multiplication (a x b = b x a). We can halve 24 to get 12 and double 6 to get 12. This simplifies the problem to 12 x 12, which is often easier to calculate:
- 24 x 6 = 12 x 12 = 144
This method is particularly useful for mental arithmetic and showcases the flexibility of multiplication.
4. Using a Multiplication Table:
For those familiar with multiplication tables, this offers a quick and efficient method. Simply locate the intersection of the 24th row and the 6th column (or vice versa) on a multiplication table to find the answer.
Visualizing 24 x 6: The Concept of Area
The equation 24 x 6 can be vividly represented using the concept of area. Imagine a rectangle with a length of 24 units and a width of 6 units. The area of this rectangle is calculated by multiplying its length and width: 24 x 6 = 144 square units. This visual representation helps solidify the understanding of multiplication as a geometric operation. You can visualize this as a grid of 24 rows and 6 columns, each representing a single square unit. Counting all the squares would yield the total area of 144.
This connection between multiplication and area is fundamental in geometry and has wide-ranging applications in various fields like construction, engineering, and design. It allows us to translate abstract mathematical concepts into concrete visual representations.
Exploring Real-World Applications of 24 x 6
The seemingly simple equation 24 x 6 has numerous practical applications in everyday life:
-
Packaging and Inventory: Imagine a box containing 24 items per layer and 6 layers stacked on top of each other. Calculating the total number of items requires multiplying 24 by 6.
-
Construction and Measurement: Calculating the area of a rectangular space (like a room or a floor) involves multiplying its length and width. If the room measures 24 feet by 6 feet, its area is 144 square feet.
-
Cooking and Baking: Many recipes involve multiplying ingredients. If a recipe calls for 6 tablespoons of an ingredient per serving, and you need to make 24 servings, you'll need to calculate 24 x 6 tablespoons.
-
Financial Calculations: Calculating the total cost of multiple items involves multiplication. If each item costs $6, and you need 24 of them, the total cost will be $144.
Beyond the Basics: Expanding on 24 x 6
The equation 24 x 6 serves as a foundation for understanding more complex mathematical concepts:
1. Factors and Multiples:
The numbers 24 and 6 are factors of 144. 144 is a multiple of both 24 and 6. Exploring factors and multiples helps in understanding the relationships between numbers and aids in simplification of larger mathematical problems.
2. Prime Factorization:
Breaking down 24 and 6 into their prime factors can provide a deeper insight into the composition of the number 144. The prime factorization of 24 is 2³ x 3, and for 6 it's 2 x 3. This allows us to explore the fundamental building blocks of numbers.
3. Algebraic Expressions:
The equation can be represented algebraically as x * y = z, where x = 24, y = 6, and z = 144. This introduces the concept of variables and equations which are central to algebra and higher-level mathematics.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes when multiplying 24 x 6?
A: A common mistake is misplacing the carry-over digits during long multiplication or incorrectly applying the distributive property. Care and attention to detail are crucial to avoiding errors.
Q: Can I use a calculator to solve 24 x 6?
A: Yes, calculators provide a quick and accurate solution, but it's crucial to understand the underlying mathematical principles involved, even when using technology.
Q: Are there other ways to represent 24 x 6 besides repeated addition and area?
A: Yes, you can use arrays (a rectangular arrangement of objects) or tree diagrams to visually represent the multiplication.
Q: How does understanding 24 x 6 help with more complex mathematical problems?
A: Mastering this simple multiplication problem strengthens foundational skills necessary for more advanced operations like division, fractions, and algebra.
Conclusion: The Significance of a Simple Equation
The seemingly simple equation, 24 x 6, is far more significant than it initially appears. It's not just a rote calculation; it's a stepping stone to understanding fundamental mathematical concepts, from area calculations to the distributive property. By exploring different methods of solving this problem and visualizing it through the lens of area, we develop a deeper appreciation for the interconnectedness of mathematical ideas. Mastering this basic equation equips learners with the skills and understanding necessary to tackle more complex mathematical challenges in the future. Furthermore, the real-world applications demonstrate the practical relevance of even the simplest mathematical concepts, illustrating their utility in diverse contexts. The journey from understanding the basic operation to appreciating its broader implications underscores the importance of building a strong foundation in mathematics.
Latest Posts
Latest Posts
-
38kmh To Mph
Sep 15, 2025
-
10 Divided 4
Sep 15, 2025
-
Brighton Clock Burning
Sep 15, 2025
-
1 25kg In Grams
Sep 15, 2025
-
Crossword Clue Sarcastic
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 24 X 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.