10 Divided 4
interactiveleap
Sep 15, 2025 · 6 min read
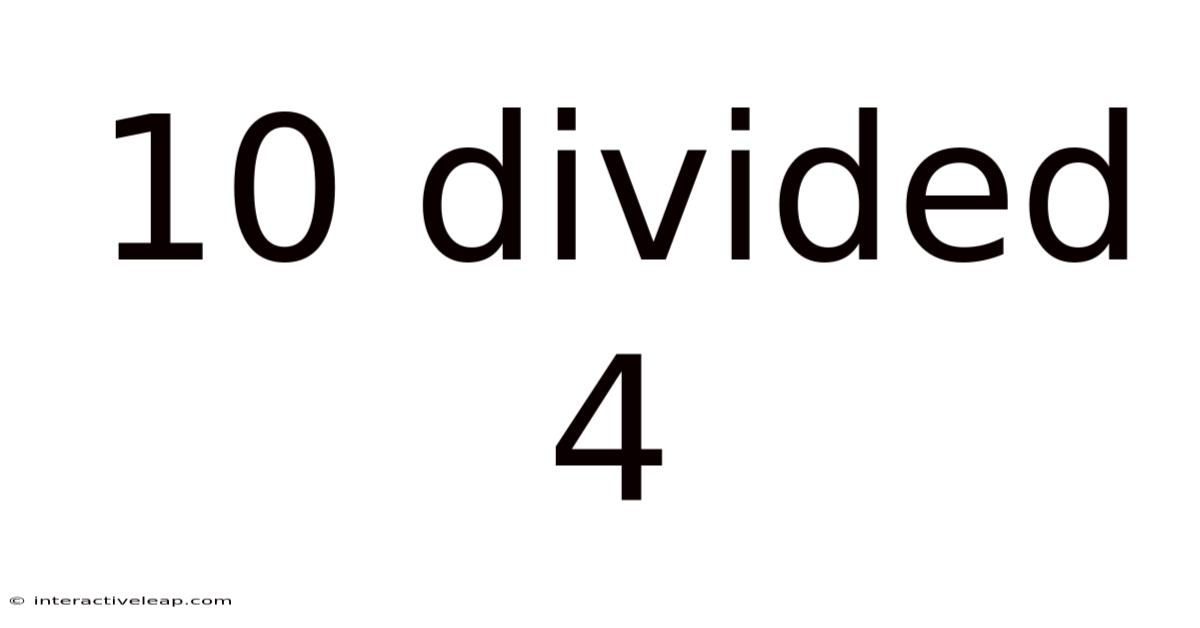
Table of Contents
Unpacking the Mystery: 10 Divided by 4
Understanding division is a fundamental building block in mathematics, crucial for everything from balancing budgets to designing skyscrapers. This seemingly simple question, "What is 10 divided by 4?", offers a gateway to exploring different aspects of division, including whole numbers, decimals, fractions, and the broader concept of remainders. This article will comprehensively unpack this calculation, providing a detailed explanation suitable for various learning levels, from elementary school to those looking to refresh their foundational math skills.
Introduction: Diving into Division
Division, at its core, is the process of splitting a quantity into equal parts. When we say "10 divided by 4," we're asking: "If we have 10 items and we want to divide them equally among 4 groups, how many items will each group receive?" This seemingly simple question opens the door to several approaches and answers, each illuminating a different facet of mathematical understanding.
Method 1: Long Division - A Step-by-Step Approach
The traditional method for solving 10 divided by 4 is long division. This method is systematic and helps visualize the process of dividing a larger number into smaller, equal parts.
-
Setup: Write the problem as 4)10. The number being divided (10) is called the dividend, and the number we are dividing by (4) is called the divisor.
-
Division: Ask yourself: "How many times does 4 go into 10?" The answer is 2. Write the '2' above the '0' in the dividend.
-
Multiplication: Multiply the quotient (2) by the divisor (4): 2 x 4 = 8. Write the '8' below the '10' in the dividend.
-
Subtraction: Subtract the result (8) from the dividend (10): 10 - 8 = 2. This '2' is the remainder.
-
Result: The result of 10 divided by 4 is 2 with a remainder of 2. We can write this as 2 R 2, or 2 remainder 2.
Method 2: Fractions - Representing Parts of a Whole
Instead of a remainder, we can express the result as a fraction. The remainder (2) becomes the numerator, and the divisor (4) becomes the denominator. Therefore, 10 divided by 4 can be represented as:
2 2/4
This fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor (2):
2 1/2
This means that 10 divided by 4 is equal to 2 and a half.
Method 3: Decimals - Expressing Parts as Tenths, Hundredths, etc.
Alternatively, we can express the remainder as a decimal. To do this, we continue the long division process by adding a decimal point and a zero to the remainder.
-
Add a Decimal: After obtaining the remainder of 2, add a decimal point to the 10 and a zero to make it 10.0.
-
Continue Division: Now we have 20. Ask: "How many times does 4 go into 20?" The answer is 5. Add this 5 after the decimal point in the quotient (above the 0).
-
Multiplication and Subtraction: Multiply 5 x 4 = 20. Subtract 20 from 20, resulting in a remainder of 0.
-
Decimal Result: The result is 2.5. This demonstrates that 10 divided by 4 is equal to 2.5.
Understanding Remainders and Their Significance
The remainder, in the context of 10 divided by 4, signifies the portion that is left over after dividing the dividend equally among the divisor. In real-world scenarios, understanding remainders is crucial. For instance, if you have 10 cookies and want to distribute them equally among 4 friends, each friend gets 2 cookies, and you have 2 cookies left over.
Real-World Applications of 10 Divided by 4
The seemingly simple calculation of 10 divided by 4 has a surprisingly wide range of real-world applications:
- Sharing Resources: Distributing items equally among people, like cookies, candies, or toys.
- Calculating Averages: Determining the average score on a test, the average price of an item, or the average speed over a journey.
- Measurement Conversions: Converting units of measurement, such as converting inches to centimeters or kilograms to pounds.
- Financial Calculations: Splitting bills equally, calculating the cost per unit of an item, or determining profit margins.
- Geometry and Spatial Reasoning: Solving problems related to area, volume, and proportions.
Different Perspectives on Division: A Deeper Dive
The act of dividing 10 by 4 can be understood from several perspectives, each offering valuable insights into the concept of division:
- Partitioning: This involves dividing a whole into a specified number of equal parts. In this case, we're partitioning 10 into 4 equal parts.
- Measurement: This involves determining how many times a smaller quantity goes into a larger quantity. We're asking how many times 4 goes into 10.
- Ratio and Proportion: Division can express a ratio. The result, 2.5, indicates a ratio of 2.5 units of one quantity to 1 unit of another.
Understanding these different perspectives strengthens the foundational understanding of division and its applications in various mathematical contexts.
Frequently Asked Questions (FAQs)
Q1: Can you explain the difference between the remainder and the decimal representation of the result?
A1: The remainder represents the leftover portion after dividing the dividend into equal groups according to the divisor. The decimal representation expresses this leftover portion as a fraction of the divisor. Both represent the same information but in different formats.
Q2: Why is it important to learn different methods of division?
A2: Learning multiple methods provides a deeper understanding of the concept. Each method highlights different aspects of division, fostering adaptability and problem-solving skills.
Q3: What if I get a very large number divided by a smaller number, and the remainder is difficult to express as a decimal?
A3: In such cases, expressing the result as a fraction is often more practical and accurate. You can also use a calculator or computer software for higher precision in decimal representation.
Q4: How does understanding 10 divided by 4 help me with more complex division problems?
A4: Mastering the fundamentals of division, as demonstrated with this simpler example, builds a solid foundation for tackling more complex problems involving larger numbers, decimals, fractions, and algebraic expressions.
Conclusion: Mastering the Fundamentals
The seemingly simple calculation of 10 divided by 4 provides a rich learning experience, showcasing different methods of division and the significance of remainders. Understanding these concepts not only strengthens mathematical skills but also provides valuable tools for solving real-world problems across diverse fields. By grasping the different approaches—long division, fractions, and decimals—and understanding the significance of remainders, you build a robust foundation in arithmetic, paving the way for more advanced mathematical concepts and applications. Remember, mastering the fundamentals is key to unlocking the power of mathematics. So keep practicing, keep exploring, and keep asking questions! Your mathematical journey is just beginning!
Latest Posts
Latest Posts
-
50 9kg In Stone
Sep 15, 2025
-
Cuba Map America
Sep 15, 2025
-
15 Of 460
Sep 15, 2025
-
150 X 7
Sep 15, 2025
-
Structured Decision Making
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 10 Divided 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.