64 Of 25
interactiveleap
Sep 16, 2025 · 5 min read
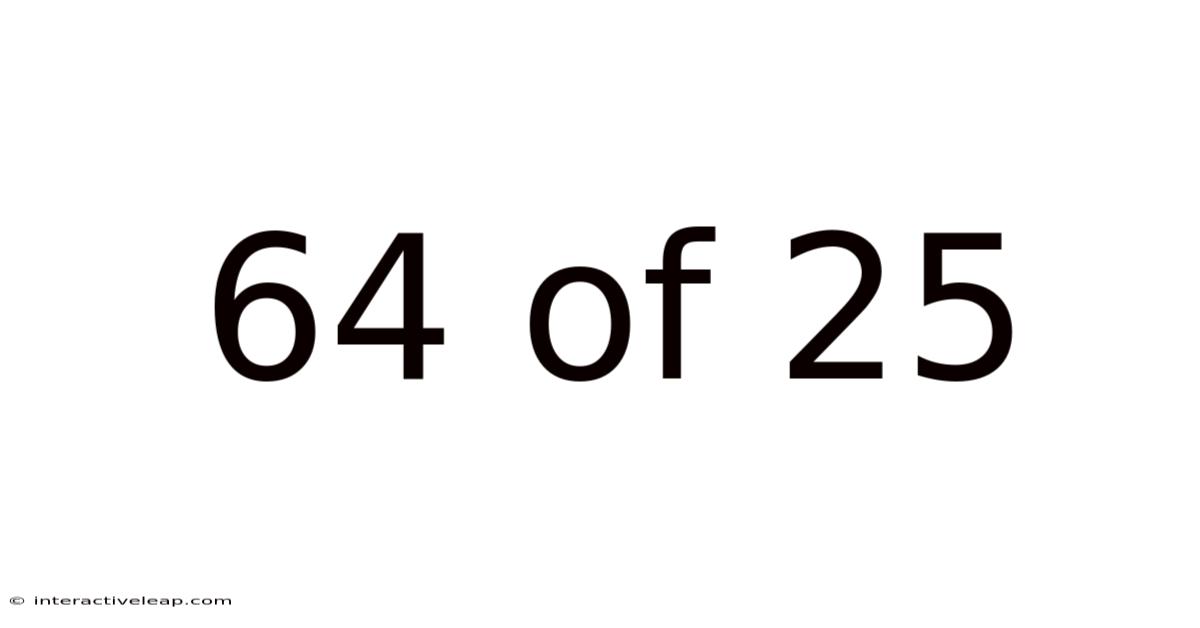
Table of Contents
Decoding the Fraction: 64/25 – A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for everything from baking a cake to complex engineering calculations. This article delves deep into the fraction 64/25, exploring its various representations, calculations, and real-world applications. We'll move beyond simple conversion and explore the deeper mathematical concepts involved, making this a valuable resource for students and anyone looking to strengthen their fractional understanding. The key terms we will be exploring are fractions, improper fractions, mixed numbers, decimal conversion, and percentage conversion.
Introduction to 64/25: An Improper Fraction
The fraction 64/25 is an improper fraction. This means the numerator (64) is larger than the denominator (25). Improper fractions represent values greater than one. Understanding improper fractions is critical for various mathematical operations and real-world applications. We will explore how to convert this improper fraction into more user-friendly formats, such as mixed numbers and decimals, and discuss the implications of each representation.
Converting 64/25 to a Mixed Number
An improper fraction can be more easily understood and used in certain contexts when expressed as a mixed number. A mixed number combines a whole number and a proper fraction. To convert 64/25 to a mixed number, we perform division:
64 ÷ 25 = 2 with a remainder of 14
This means that 64/25 can be written as 2 14/25. The whole number 2 represents how many times 25 goes into 64 completely, and the remaining 14/25 represents the fractional part. This representation is often preferred when dealing with quantities that involve whole units and parts of units. For example, if you have 64 quarters (25 cents each), you have 2 dollars and 14 cents (14/25 of a dollar).
Converting 64/25 to a Decimal
Converting a fraction to a decimal involves dividing the numerator by the denominator. In this case:
64 ÷ 25 = 2.56
Therefore, 64/25 is equivalent to 2.56. The decimal representation is useful for calculations involving decimal numbers, and provides a clear numerical value. Decimals are commonly used in scientific calculations, financial applications, and everyday measurements.
Converting 64/25 to a Percentage
Percentages express a fraction as a proportion of 100. To convert 64/25 to a percentage, we first convert it to a decimal (as shown above, it's 2.56) and then multiply by 100%:
2.56 x 100% = 256%
This means that 64/25 represents 256% of a whole. Percentages are widely used to express proportions, ratios, and rates of change, making this representation valuable in various fields.
Visual Representation of 64/25
Visualizing fractions can greatly aid understanding. Imagine a circle divided into 25 equal parts. To represent 64/25, you would need two complete circles (50 parts) and then an additional 14 parts of a third circle. This visual representation clearly demonstrates that 64/25 is more than one whole.
Real-World Applications of 64/25
The fraction 64/25, in its various forms (mixed number, decimal, percentage), has various practical applications:
- Finance: Calculating interest rates, proportions of investments, or shares of profits. For instance, a 256% return on an investment.
- Measurement: Expressing quantities that are more than a whole unit. For example, 2.56 meters, representing slightly more than two and a half meters.
- Baking: Scaling up or down recipes. If a recipe calls for 25 grams of flour, and you need 64 grams, you'd be using 64/25 times the original amount.
- Construction: Calculating dimensions, material quantities, and scaling up blueprints.
Mathematical Operations with 64/25
Understanding how to perform various mathematical operations with 64/25 is essential. Let's explore some examples:
- Addition: Adding 64/25 to another fraction requires finding a common denominator. For example, adding 64/25 + 1/5 would involve converting 1/5 to 5/25, resulting in 69/25.
- Subtraction: Similar to addition, subtraction requires a common denominator. Subtracting a fraction from 64/25 involves finding a common denominator and then subtracting the numerators.
- Multiplication: Multiplying 64/25 by another fraction involves multiplying the numerators together and the denominators together. For example, 64/25 x 3/4 = 192/100, which can be simplified.
- Division: Dividing 64/25 by another fraction involves inverting the second fraction and multiplying. For example, 64/25 ÷ 2/5 would be 64/25 x 5/2 = 320/50, which can be simplified.
Simplifying Fractions: A Crucial Step
While 64/25 is already in its simplest form as an improper fraction, the results of operations involving it might not be. Simplifying fractions involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. This reduces the fraction to its lowest terms, making it easier to understand and work with.
Working with Different Representations
It's crucial to remember that the choice of representation (improper fraction, mixed number, decimal, percentage) depends on the specific context and the type of calculations involved. Sometimes, a mixed number offers a clearer intuitive understanding, while a decimal might be more suitable for calculations. Choosing the right representation makes mathematical operations more efficient and accurate.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 64/25?
A: 64/25 is already in its simplest form as an improper fraction.
Q: How do I convert 64/25 to a percentage?
A: Divide 64 by 25 (resulting in 2.56) and then multiply by 100% to get 256%.
Q: Can 64/25 be simplified further?
A: No, 64 and 25 have no common factors other than 1.
Q: What is the mixed number equivalent of 64/25?
A: The mixed number equivalent is 2 14/25.
Q: What is the decimal equivalent of 64/25?
A: The decimal equivalent is 2.56.
Conclusion: Mastering Fractions – A Continuous Journey
Understanding fractions, including improper fractions like 64/25, is a fundamental skill that extends beyond the classroom. Through understanding its various representations and applications, we can confidently tackle a wide range of mathematical problems and real-world situations. Remember to choose the most appropriate representation based on the context and perform necessary calculations with precision. The journey of mastering fractions is a continuous one, but with consistent practice and a clear understanding of the underlying concepts, you can develop proficiency and confidence in working with fractions of any complexity.
Latest Posts
Latest Posts
-
Poet And Musician
Sep 16, 2025
-
57cm In Inch
Sep 16, 2025
-
80cm To Mm
Sep 16, 2025
-
X 6 2
Sep 16, 2025
-
25 Of 3
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 64 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.