64 2 3
interactiveleap
Sep 22, 2025 · 5 min read
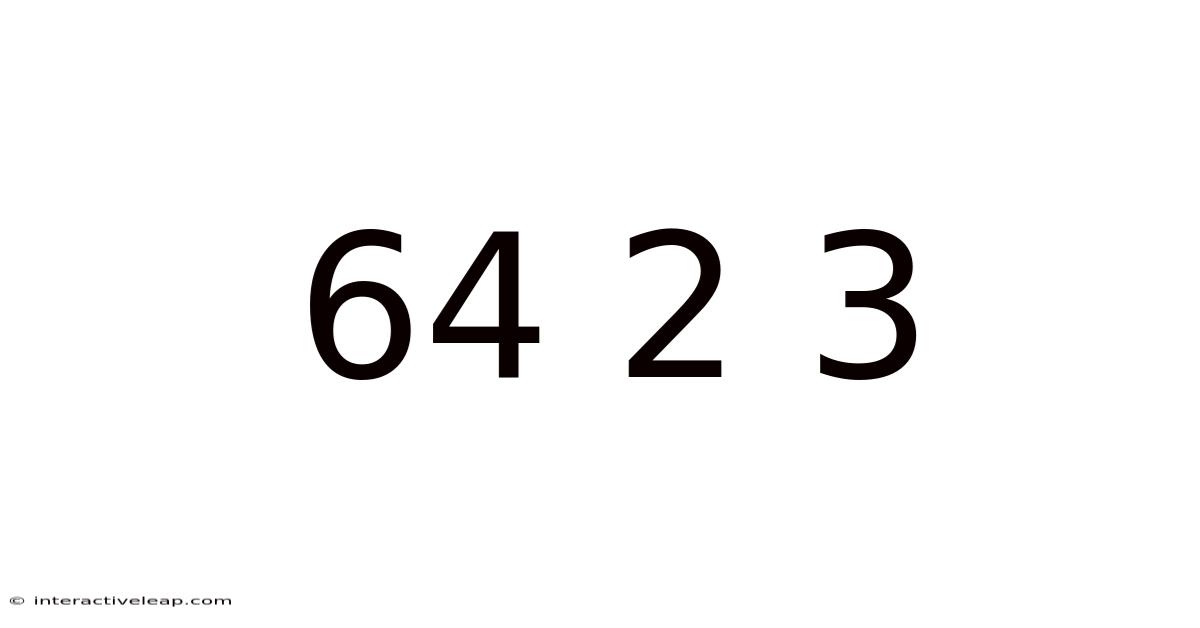
Table of Contents
Decoding the Enigma: A Deep Dive into the Number Sequence "64 2 3"
The seemingly simple number sequence "64 2 3" holds a fascinating potential for exploration. While it lacks immediate context, its ambiguity allows for diverse interpretations, making it a rich ground for mathematical, logical, and even creative analysis. This article will delve into various approaches to understanding this sequence, exploring potential patterns, underlying principles, and ultimately, the power of pattern recognition in problem-solving. We will move beyond a simple answer and strive to understand the process of decoding such numerical puzzles.
Potential Interpretations and Approaches
The absence of explicit context makes "64 2 3" open to multiple interpretations. We can approach it from several angles:
1. Mathematical Sequences and Series:
The most straightforward approach is to search for a mathematical relationship between the numbers. This could involve:
- Arithmetic Progression: Is there a consistent difference between consecutive numbers? Clearly, there isn't a simple arithmetic progression here (64-2 = 62, 2-3 = -1).
- Geometric Progression: Is there a consistent ratio between consecutive numbers? Again, this doesn't appear to be the case.
- Fibonacci-like Sequences: Fibonacci sequences involve adding the previous two numbers to get the next. While this doesn't directly apply, variations or generalizations of Fibonacci sequences could potentially incorporate these numbers, although finding a natural fit would require significant manipulation.
- Polynomial Relationships: More complex relationships might exist. We could potentially fit a polynomial function to these four points, although this approach would lack elegance and predictive power unless a meaningful pattern emerges. For example, finding a cubic polynomial that fits these four points is mathematically possible, but this is just curve fitting without inherent meaning.
2. Base Conversion and Number Systems:
Another approach is to consider different number systems. The sequence could be representing numbers in a base other than 10 (decimal).
-
Binary, Octal, Hexadecimal: Converting these numbers to binary, octal, or hexadecimal doesn't immediately reveal a clear pattern. However, if the sequence represents parts of larger numbers expressed in different bases, patterns might emerge upon closer inspection. For example, 64 in decimal is 1000000 in binary, but this doesn't immediately connect to the other numbers.
-
Mixed Base Systems: The possibility of using a mixed-base system – where different numbers in the sequence are represented in different bases – cannot be ruled out. This would require more complex analysis.
3. Coded Messages and Cryptography:
A more imaginative approach treats the sequence as a coded message. This could involve:
- Substitution Ciphers: Each number might represent a letter or symbol according to a specific substitution key. Without a key, however, this approach is highly speculative.
- Polyalphabetic Substitution: A more sophisticated approach would involve using different substitution alphabets for each number. This would require further information to decipher.
4. Combinatorial and Permutational Analysis:
The sequence could represent choices or arrangements.
- Combinations and Permutations: The numbers could represent the number of combinations or permutations of a set. For instance, '64' could represent the number of ways to arrange a certain set of objects. However, without additional context, this remains purely speculative.
5. Geometric or Spatial Representation:
It's also plausible to consider a geometric interpretation.
- Coordinate Systems: Could "64 2 3" represent coordinates in a multi-dimensional space? This is possible, but again, it lacks context for meaningful interpretation.
A Deeper Dive into Mathematical Possibilities
Let's delve deeper into the mathematical avenues, focusing on approaches that go beyond simple arithmetic or geometric progressions.
Exploring Polynomial Relationships:
As mentioned earlier, we can attempt to fit a polynomial function to the data points (1, 64), (2, 2), (3, 3). This would involve solving a system of equations. However, the resulting polynomial would likely be complex and lack inherent meaning unless a clear underlying pattern or relationship is established independently. The goal is not just to fit a curve but to find a function that reflects a natural process or law.
Generalized Fibonacci Sequences:
Standard Fibonacci sequences (where each term is the sum of the two preceding terms) clearly don't fit. However, we could explore generalized Fibonacci sequences. These involve altering the rule for generating the next term. For instance, we could explore sequences where:
- The next term is a function of the previous terms (e.g., a weighted sum, or a more complex function).
- The sequence incorporates a modular arithmetic operation (e.g., the next term is the remainder when a function of the previous terms is divided by a specific number).
Discovering such a generalized Fibonacci sequence would require systematic exploration and testing of different generating rules.
Exploring Prime Numbers and Factorization:
Analyzing the prime factorization of the numbers can be insightful. 64 = 2<sup>6</sup>. This reveals a strong relationship with the number 2. However, the presence of 2 and 3 – which are both prime numbers – doesn't readily suggest a direct mathematical relationship, at least not without introducing more sophisticated mathematical tools.
The Importance of Context and Additional Information
The key limitation in analyzing "64 2 3" is the lack of context. Without further information, any interpretation remains highly speculative. To unlock the true meaning of this sequence, we need additional clues. Such clues might include:
- The Source: Where did this sequence come from? A math problem? A code? A game?
- Surrounding Numbers or Data: Are there other numbers or data points associated with this sequence?
- Instructions or Rules: Were there any specific instructions or rules provided alongside the sequence?
The absence of this crucial context highlights the importance of thoroughly understanding the source and background of any numerical sequence before attempting to decipher its meaning.
Conclusion: The Power of Pattern Recognition and Critical Thinking
Deciphering numerical sequences like "64 2 3" is a valuable exercise in critical thinking and pattern recognition. It highlights the need for a systematic approach, exploring various possibilities, and recognizing the limitations of analysis without sufficient context. While we have explored numerous mathematical and logical avenues, the ultimate solution requires additional information to confirm a meaningful interpretation. The process itself, however, is an invaluable lesson in problem-solving and the importance of carefully considering all possible approaches. The journey of investigation, even without a definitive answer, significantly expands our understanding of pattern recognition, mathematical analysis, and the creative problem-solving process. The ambiguity of this sequence, ultimately, is its most engaging feature.
Latest Posts
Latest Posts
-
Giant Covalent Lattice
Sep 22, 2025
-
96 Divided 3
Sep 22, 2025
-
15 Of 67
Sep 22, 2025
-
Radius Versus Diameter
Sep 22, 2025
-
Thomas Struth Photographer
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 64 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.