96 Divided 3
interactiveleap
Sep 22, 2025 · 6 min read
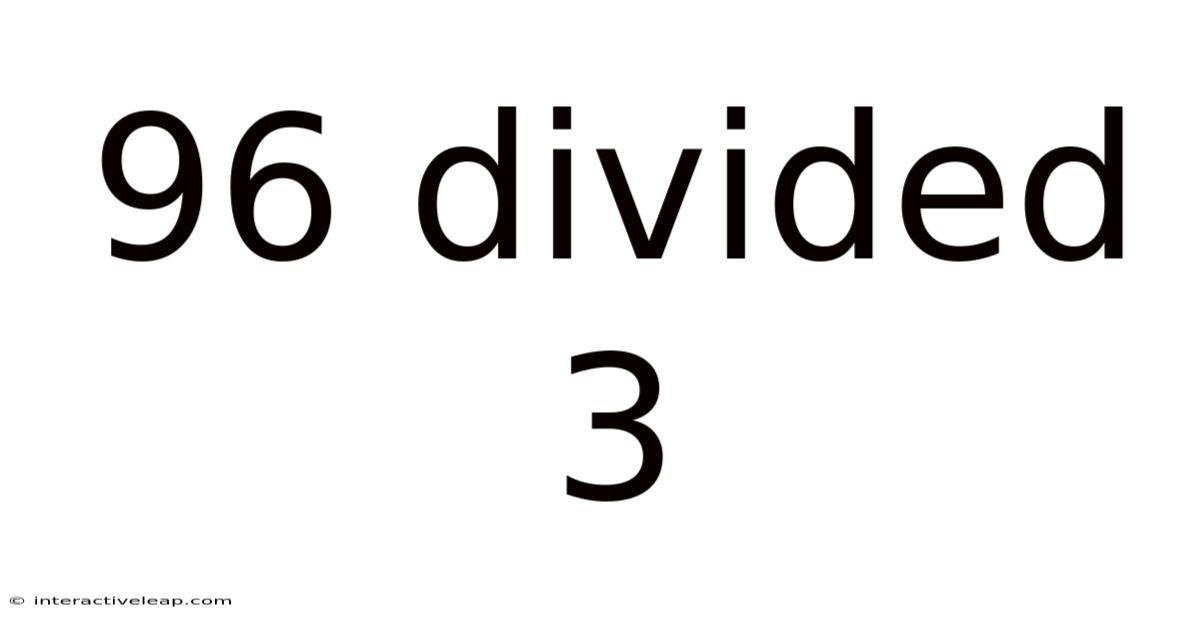
Table of Contents
96 Divided by 3: A Deep Dive into Division and its Applications
This article explores the seemingly simple calculation of 96 divided by 3, delving beyond the basic arithmetic to uncover the underlying principles of division, its various methods, real-world applications, and its connection to other mathematical concepts. Understanding this fundamental operation unlocks a deeper appreciation of mathematics and its practical uses. We will explore different approaches to solving this problem, clarifying the process for learners of all levels.
Understanding Division: The Foundation
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts or groups. In the context of 96 divided by 3 (represented as 96 ÷ 3 or 96/3), we're asking: "How many times does 3 fit into 96?" or "If we divide 96 into 3 equal groups, how many will be in each group?" The result of this operation is called the quotient. Any remaining amount after the equal division is called the remainder. In this case, because 96 is perfectly divisible by 3, there will be no remainder.
Methods for Solving 96 ÷ 3
Several methods can be employed to calculate 96 divided by 3. Let's explore a few:
1. Long Division: A Step-by-Step Approach
Long division is a systematic method that works for dividing larger numbers. Here's how it's applied to 96 ÷ 3:
-
Set up the problem: Write 96 inside the long division symbol (⟌) and 3 outside.
-
Divide the tens digit: How many times does 3 go into 9? The answer is 3 (3 x 3 = 9). Write 3 above the 9 in the quotient.
-
Multiply and subtract: Multiply the quotient digit (3) by the divisor (3): 3 x 3 = 9. Subtract this result from the tens digit of the dividend (9 - 9 = 0).
-
Bring down the ones digit: Bring down the ones digit of the dividend (6) next to the 0.
-
Divide the ones digit: How many times does 3 go into 6? The answer is 2 (3 x 2 = 6). Write 2 above the 6 in the quotient.
-
Multiply and subtract: Multiply the quotient digit (2) by the divisor (3): 2 x 3 = 6. Subtract this from the remaining number (6 - 6 = 0).
-
The quotient is 32: Since there's no remainder, the final answer is 32. Therefore, 96 ÷ 3 = 32.
2. Repeated Subtraction: A Conceptual Approach
This method visually demonstrates the concept of division. We repeatedly subtract the divisor (3) from the dividend (96) until we reach zero. The number of times we subtract is the quotient.
96 - 3 = 93 93 - 3 = 90 90 - 3 = 87 ...and so on until you reach 0. Counting the number of subtractions will yield the answer, 32. While effective for smaller numbers, this method becomes less efficient for larger numbers.
3. Mental Math: Utilizing Number Sense
For those comfortable with multiplication tables, mental math can be the quickest method. Knowing that 3 x 30 = 90 and 3 x 2 = 6, we can quickly deduce that 3 x 32 = 96. Therefore, 96 ÷ 3 = 32. This approach leverages number sense and pattern recognition.
The Significance of 96 ÷ 3: Real-World Applications
The seemingly simple calculation of 96 ÷ 3 finds applications in numerous real-world scenarios:
-
Equal Sharing: If you have 96 candies and want to divide them equally among 3 friends, each friend receives 32 candies.
-
Unit Conversions: Imagine you have 96 inches of fabric and need to convert it to feet (since 1 foot = 12 inches). You might first divide 96 by 3 to simplify calculations before further conversion.
-
Resource Allocation: If a project requires 96 hours of work to be completed by 3 people, each person needs to dedicate 32 hours.
-
Averages: If 3 students scored a total of 96 points on a test, their average score is 32 points.
-
Geometry: The area of a rectangle might be 96 square units, and one side is 3 units long. Using division, we find the length of the other side (32 units).
These examples highlight the practical relevance of even seemingly basic division problems.
Expanding the Concept: Connecting to Other Mathematical Ideas
The calculation 96 ÷ 3 is not just an isolated arithmetic problem; it connects to broader mathematical concepts:
-
Factors and Multiples: The numbers 3 and 32 are factors of 96, while 96 is a multiple of both 3 and 32. Understanding factors and multiples helps in simplifying calculations and solving more complex problems.
-
Fractions: The problem can also be represented as the fraction 96/3, which simplifies to 32/1, or simply 32. This connection strengthens the understanding of the relationship between division and fractions.
-
Algebra: Division is a crucial component in solving algebraic equations. For instance, if 3x = 96, dividing both sides by 3 yields x = 32.
-
Modular Arithmetic: In modular arithmetic (clock arithmetic), the remainder after division plays a crucial role. Although 96 ÷ 3 has no remainder, understanding remainders is important for concepts like congruences.
Frequently Asked Questions (FAQ)
Q1: What if the number wasn't perfectly divisible by 3? Would there be a remainder?
A1: Yes, if the dividend wasn't perfectly divisible by the divisor, there would be a remainder. For instance, if we divide 97 by 3, the quotient is 32, and the remainder is 1 (32 x 3 + 1 = 97).
Q2: Are there other ways to check if 96 is divisible by 3?
A2: Yes! A number is divisible by 3 if the sum of its digits is divisible by 3. In 96, 9 + 6 = 15, and 15 is divisible by 3 (15 ÷ 3 = 5). This divisibility rule is a handy shortcut.
Q3: How can I improve my division skills?
A3: Practice is key! Start with simpler division problems and gradually increase the difficulty. Utilize different methods to reinforce your understanding and find the approach that suits you best. Focus on mastering multiplication tables as they are fundamental to division. Also, consider using online resources, educational apps, or working with a tutor.
Conclusion: Beyond the Numbers
The seemingly simple arithmetic problem of 96 divided by 3 opens a window into the world of mathematics, revealing its inherent logic, structure, and practical applications. By understanding the different methods of solving this problem and its connection to broader mathematical concepts, we gain a deeper appreciation for the power and versatility of this fundamental operation. Mastering division isn't just about getting the right answer; it's about developing a strong foundation in mathematical reasoning and problem-solving skills that are essential in various aspects of life. This fundamental skill serves as a building block for more advanced mathematical concepts and real-world problem-solving. Remember, consistent practice and a curious mindset are key to unlocking your full mathematical potential.
Latest Posts
Latest Posts
-
125g To Ounces
Sep 22, 2025
-
16 Of 88
Sep 22, 2025
-
52f In C
Sep 22, 2025
-
48 4kg In Stone
Sep 22, 2025
-
125g Into Oz
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 96 Divided 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.